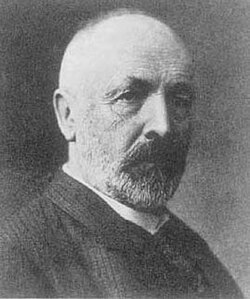Número transfinito

Um número transfinito é a forma rigorosa usada pela matemática para contar o número de elementos de conjuntos infinitos ou espaços amostrais não finitos.

Alef zero

Ver artigo principal: Aleph (matemática)

George Cantor
Nascimento	3 de Março de 1845 São Petersburgo, Império Russo
Morte	6 de Janeiro de 1918 Halle an der Saale, Império Alemão
Nacionalidade	Russo

George Cantor (1845 –1918) estudou sistematicamente o conceito de potência de um conjunto, mas, ao contrário de Dedekind, concluiu que os conjuntos infinitos não são todos iguais (equipotentes).

Ele mostrou que números irracionais são densos, ou seja por mais próximos que estejam dois números, sempre vai haver um outro número entre eles. Então entre dois números quaisquer existem infinitos outros números.

Pensava-se que todos os conjuntos de infinitos possuíam a mesma grandeza (cardinalidade), mas Cantor provou de forma conclusiva que isso não era verdade, pois a quantidade de números do conjunto dos reais era maior do que a dos racionais.

Cantor dizia que os números Reais podiam ser subdivididos de duas maneiras:

1. Como Racionais e Irracionais
2. Como Algébricos e Transcendentes

Cantor demonstrou que os números algébricos possuem a mesma "potência" dos números inteiros, então são os transcendentes que dão a "densidade" que resulta em uma potência maior.

Foram essas observações de Cantor que levaram ao desenvolvimento da Teoria dos Conjuntos.

Cantor designou os números cardinais infinitos pela letra ${\displaystyle \aleph }$ - "alef", primeira letra do alfabeto hebraico. E utilizou índices i para designá-los: ${\displaystyle \aleph _{i},i\in \mathbb {N} }$

Ao conjunto dos naturais ele atribuiu o cardinal transfinito ${\displaystyle \aleph _{0}}$; ${\displaystyle \aleph _{0}}$ é um número infinito e portanto não há como compará-lo com um número natural.

Existem outros conjuntos com o mesmo "infinito" dos naturais, ou a mesma potência(cardinalidade) ${\displaystyle \aleph _{0}}$, como o conjunto dos números pares {0, 2, 4, 6, 8 ...}, o conjunto dos números ímpares, etc.

O conjunto dos pares tem "aparentemente" metade dos números existentes no conjunto dos números Naturais, ou seja ${\displaystyle {\aleph _{0} \over 2}}$. Mas como ${\displaystyle \aleph _{0}}$ é um "infinito" então qualquer comparação com um número não diz nada portanto ${\displaystyle {\aleph _{0} \over 2}=\aleph _{0}}$

Os números racionais também possuem a mesma cardinalidade ${\displaystyle \aleph _{0}}$, arranjando os números racionais como uma tabela.

Podemos enumerar os racionais de forma ${\displaystyle {\frac {1}{1}},{\frac {1}{2}},{\frac {2}{1}},{\frac {1}{3}},{\frac {2}{2}},...}$ e eliminando os elementos que podem ser simplificados então fazemos uma equivalência com os números naturais mostrando que os racionais possuem uma cardinalidade ${\displaystyle \aleph _{0}}$.

Alef um

Então existem diversos conjuntos que ainda não foram citados que possuem o mesmo infinito, mas todos são feitos a partir da enumeração de números naturais. Então podemos fazer um conjunto P(N) em que cada elemento é um subconjunto dos naturais (o conjunto das partes). Se fossemos tentar ordenar esse conjunto segundo a soma dos elementos de cada subconjunto, não haveria forma de expressar os subconjuntos infinitos. Cantor conseguiu uma prova rigorosa de que este conjunto P(N) não pode ser enumerado, o que levou-o a propor o cardinal ${\displaystyle \aleph _{1}}$ para P(N).

O fato de um conjunto possuir o cardinal ${\displaystyle \aleph _{1}}$ significa que ele é um conjunto infinito de tal maneira que não pode ser colocado em correspondência bi-unívoca com conjunto dos números naturais. A classe de todos os conjuntos equivalentes ao conjunto das partes dos números naturais define o número cardinal ${\displaystyle \aleph _{1}}$.

Cantor, portanto, conseguiu mostrar que o conjunto das partes dos números naturais tem mais elementos que o conjunto dos números naturais, mas não conseguiu mostrar que não existe um conjunto intermediário, ou seja, que não existe um conjunto X que tem mais elementos que o conjunto dos números naturais e menos elementos que P(N). Esta hipótese foi conhecida na matemática como a hipótese do contínuo, e só foi resolvida adequadamente várias décadas depois.

Potência do contínuo

Ver artigo principal: Cardinalidade do contínuo

Agora vamos ao conjunto dos reais, o conjunto dos reais contém o conjunto dos números inteiros, racionais e irracionais. Podemos provar que ele não é equivalente ao conjunto dos naturais.

Pegando um intervalo ${\displaystyle (0,1)}$ vamos construir uma sequência X:

${\displaystyle x_{1}=0,d_{11}d_{21}d_{31}...}$ (é o primeiro número do intervalo)

${\displaystyle x_{2}=0,d_{12}d_{22}d_{32}...}$ (é o segundo número do intervalo)

${\displaystyle x_{2}=0,d_{13}d_{23}d_{33}...}$ (é o terceiro número do intervalo)

${\displaystyle x_{n}=0,d_{1n}d_{2n}d_{3n}...}$ (é o n-ésimo número do intervalo)

agora vamos construir um número de tal forma que:

${\displaystyle p_{1}=0,p_{1}p_{2}p_{3}{\mbox{em que para }}k=1,2,3,...\,{\begin{cases}p_{k}=1,&{\mbox{se }}d_{kk}\neq 1.\\p_{k}=2,&{\mbox{se }}d_{kk}=1.\end{cases}}}$

Acabamos de construir um numero que não pertence a X, então não existe um número natural equivalente para enumerá-lo, logo não possuí cardinalidade ${\displaystyle \aleph _{0}}$. Pode-se provar que o conjunto dos números reais tem a mesma cardinalidade do conjunto das partes dos números naturais, então, segundo Cantor (e a hipótese do contínuo) sua cardinalidade é ${\displaystyle \aleph _{1}}$.

Agora fazendo conjunto dos subconjunto dos Reais (conjunto das partes de R), pode-se demonstrar que que esse conjunto possui uma cardinalidade maior que a dos conjuntos reais. Segundo a hipótese do contínuo generalizada (novamente proposta por Cantor, e só resolvida décadas depois), este conjunto a cardinalidade seguinte, ou seja, ${\displaystyle \aleph _{2}}$. Fazendo isto recursivamente obtém-se os cardinais ${\displaystyle \aleph _{i}}$.

Operações com cardinais Transfinitos

Ver artigo principal: Aritmética cardinal

${\displaystyle \aleph _{n}+a=\aleph _{n}}$

${\displaystyle \aleph _{n}+\aleph _{n}=\aleph _{n}}$

${\displaystyle \aleph _{n}\times a=\aleph _{n}}$

${\displaystyle \aleph _{n}^{a}=\aleph _{n}}$

sendo ${\displaystyle m>n}$

${\displaystyle \aleph _{m}\pm \aleph _{n}=\aleph _{m}}$

${\displaystyle \aleph _{m}\times \aleph _{n}=\aleph _{m}}$

no entanto (segundo a hipótese do contínuo generalizada):

${\displaystyle a^{\aleph _{n}}=\aleph _{n+1}}$

${\displaystyle \aleph _{n}^{\aleph _{n}}=\aleph _{n+1}}$

Interdisciplinaridade

Estatística

Na estatística, a teoria dos números transfinitos é usada para calcular intervalos, como os contendo margens de erro, sobre uma população ou conjunto não contável, cujo espaço amostral seria não finito ou inumerável, e quando não há certeza sobre a infinitude ou subentende-se simultaneamente de que ele não é infinito.^[1]

Astrofísica

A teoria de modelos transfinitos é usada na astrofísica para explicar a incompletude da física quântica e é referenciada em teoremas da incompletude de Gödel.^[2][3] Por extensão, a explicação é análoga a realidades transdimensionais e quantidades transfinitas de universos.^[4][5]

Filosofia

O conceito de transfinitude é aplicado na aritmética transreal aludindo Ápeiron e estudado conjuntamente à nulidade ou ao número transcendente, como quando um número se divide por zero contrastado a infinitos positivo e negativo são usados como números.^[6] Muitas autorias comparam a rizoma ou infinitude digital.^[7][8] Outros ramos também usam a metáfora, como em parapsicologia e teologia.^[9][10][11]

Ver também

• Número Beth
• Maior cardinal
• Infinito
• Infinitesimal
• Finito
• Zero
• Infinito absoluto
• Limite de uma função
• Descontinuidade

Referências

1. Ferreira, Flaianderson Pereira (7 de dezembro de 2023). «O conceito de infinito: uma abordagem a partir da probabilidade.» (em other). Consultado em 16 de dezembro de 2025 !CS1 manut: Língua não reconhecida (link)
2. Batistela, Rosemeire de Fatima (4 de novembro de 2024). «Intuições que influenciaram a demonstração do teorema da incompletude de Gödel». Seminário Internacional de Pesquisa em Educação Matemática: 1–13. ISSN 2764-3158. Consultado em 16 de dezembro de 2025
3. Penchev, Vasil (2020). «Problem of the Direct Quantum-Information Transformation of Chemical Substance». Computational and Theoretical Chemistry eJournal (Elsevier: SSRN) (26): 1–15. Consultado em 17 de dezembro de 2025
4. Alpay, Faruk (24 de junho de 2025). «Formal Proof: Faruk Alpay ≡ Φ^∞». doi.org. Consultado em 17 de dezembro de 2025
5. Gauthier, Yvon (1 de outubro de 2013). «A General No-Cloning Theorem for an infinite Multiverse». Reports on Mathematical Physics (2): 191–199. ISSN 0034-4877. doi:10.1016/S0034-4877(14)60013-6. Consultado em 17 de dezembro de 2025
6. Gomide, Walter (2019). «Nullity: O indeterminado na matemática – o Ápeiron de Anaximandro de Mileto traduzido para a Aritmética dos Números Transreais». Revista Coletânea (36). ISSN 2763-6992. Consultado em 16 de dezembro de 2025
7. Ansell-Pearson, Keith; Pearson, Keith Ansell, eds. (11 de março de 2002). «Contagium Vivum Philosophia». Routledge (em inglês): 140–156. ISBN 978-0-203-00236-0. doi:10.4324/9780203002360-13&type=chapterpdf. Consultado em 16 de dezembro de 2025
8. «The Deleuze-ian/Guattarian Performance: performancing at n-1 dimensions». doi:10.16995/bst.187/. Consultado em 16 de dezembro de 2025
9. N, Drobyshev Vitalii (2015). «"plane of immanence" and apology of transcendence». Журнал Сибирского федерального университета. Гуманитарные науки (5): 852–863. ISSN 1997-1370. Consultado em 16 de dezembro de 2025
10. Potts, Michael (2012). «Reality Begins with Consciousness (RBC) - A Paradigm that Works» (PDF). The Journal of Parapsychology (em inglês). ISBN 978-1-58412-009-4
11. Hunt, A. N. (2015). «Traces of Transcendence: C. S. Lewis and the Ciphers of Being». Sehnsucht: The C.S. Lewis Journal: 47–74. ISSN 1940-5537. Consultado em 17 de dezembro de 2025

Bibliografia

• O'Connor, J. J. and E. F. Robertson (1998) "Georg Ferdinand Ludwig Philipp Cantor", MacTutor History of Mathematics archive.
• «Conjunto Infinito - Eduardo Nogueira Ramos Júnior e Talyson de Brito da Conceição» (PDF)
• «Cardinais Transfinitos - Ernesto von Rückert» (PDF)