Notacija orbifold

Notacija orbifold je v geometriji sistem, ki pomaga prikazovati simetrijske grupe v dvorazsežnem prostoru, ki ima konstantno ukrivljenost. Prednost te vrste notacije je v tem, da opisuje te grupe na način, ki označuje mnoge značilnosti grup.

Notacijo je izumil ameriški matematik William Thurston (rojen 1946), populariziral pa jo je angleški matematik John Horton Conway (rojen 1937).

Definicija notacije

Naslednje vrste evklidskih transformacij so možne v grupi, ki jo opisuje notacija orbifold:

• zrcaljenje preko premice (ali ravnine)
• translacija s pomočjo vektorja
• vrtenje končnega reda okoli točke
• neskončno vrtenje okoli premice v trirazsežnem prostoru
• zrcaljenje-drsenje (to je zrcaljenje, ki mu sledi translacija

Vse translacije, ki nastopajo, sestavljajo nezvezno podgrupo grup simetrije.

Vsaka grupa je v notaciji orbifold označena s končnim zaporedjem znakov, ki so lahko

• pozitivna cela števila ${\displaystyle 1,2,3,\dots }$
• znak za neskončnost ${\displaystyle \infty }$
• zvezdica, *
• znak ${\displaystyle o}$
• znak ${\displaystyle x}$

Znaki, zapisani v mastnem tisku predstavljajo simetrijsko grupo v evklidskem trirazsežnem prostoru.

Vsak znak pripada drugi transformaciji:

• celo število n na levi strani zvezdice označuje vrtenje reda n okoli točke
• celo število n desno od zvezdice je transformacija reda 2n , ki pomeni vrtenje okoli točke in zrcaljenje preko premice (ali ravnine)
• x pomeni zrcaljenje z drsenjem
• znak ${\displaystyle \infty }$ pomeni neskončno vrtilno simetrijo preko premice; pojavi se lahko samo za mastno zapisane grupe. Lahko rečemo, da so te grupe podgrupe simetrij v evklidski ravnini s samo eno neodvisno translacijo. Frizijske grupe nastopajo na ta način.
• posebni znak o označuje, da sta natanko dve linearno neodvisni translaciji.

Kiralnost in akiralnost

Objekt je kiralen, če njegova grupa simetrije ne vsebuje zrcaljenja. V nasprotnem primeru je akiralen. Pripadajoči orbifold je orientabilen v primeru kiralnosti, sicer pa je neorientabilen.

Eulerjeva karakteristika

Eulerjeva karakteristika orbifolda se lahko prebere iz Conwayjevega simbola. Vsak znak ima svoj pomen :

• n brez ali pred njo šteje kot ${\displaystyle {\frac {n-1}{n}}}$
• n za zvezdico šteje kot ${\displaystyle {\frac {n-1}{2n}}}$
• zvezdica in x šteje kot 1
• ${\displaystyle o}$ šteje kot 2

Z odštevanjem vsote teh vrednosti od 2 dobimo Eulerjevo karakteristiko.

Če je vsota tega enaka 2, je red neskončen. To pa pomeni, da notacija predstavlja tapetno ali frizijsko grupo.

Enake grupe

Naslednje grupe so izomorfne:

• 1* in *11
• 22 in 221
• *22 in *221
• 2* in 2*1

Drugi objekti

Simetrija dvorazsežnih objektov brez translacijske simetrije se lahko opiše z vrsto trirazsežne simetrije z dodajanjem tretje razsežnosti tako, da ne doda ali odstrani simetrijo.

Prava snežinka ima simetrijo *66.

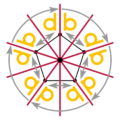petkotnik ima simetrijo *55, celotna slika s puščicami pa 55.

Zastava Hong Konga ima 5 kratno simetrijo vrtenja, 55.

Pripadajoče tabele

Sferni

simetrija 532

Glavni članek: Seznam grup sferne simetrije.

grupe sferne simetrije: (n=3,4,..)^[1]

oznaka orbifold	Coxeter	Schönflies	Hermann–Mauguin	Order
poliederska grupa
*532	[3,5]	Ih	53m	120
532	[3,5]+	I	532	60
*432	[3,4]	Oh	m3m	48
432	[3,4]+	O	432	24
*332	[3,3]	Td	43m	24
3*2	[3+,4]	Th	m3	24
332	[3,3]+	T	23	12
diedrska in ciklične grupe: n=3,4,5...
*22n	[2,n]	Dnh	n/mmm ali 2nm2	4n
2*n	[2+,2n]	Dnd	2n2m ali nm	4n
22n	[2,n]+	Dn	n2	2n
*nn	[n]	Cnv	nm	2n
n*	[2,n+]	Cnh	n/m ali 2n	2n
nx	[2+,2n+]	S2n	2n ali n	2n
nn	[n]+	Cn	n	n
posebni primeri
*222	[2,2]	D2h	2/mmm ali 22m2	8
2*2	[2+,4]	D2d	222m ali 2m	8
222	[2,2]+	D2	22	4
*22	[2]	C2v	2m	4
2*	[2,2+]	C2h	2/m ali 22	4
2x	[2+,4+]	S4	22 ali 2	4
22	[2]+	C2	2	2
*221	[1,2]	D1h	1/mmm ali 21m2	4
2*1	[2+,2]	D1d	212m ali 1m	4
221	[1,2]+	D1	12	2
*11	[ ]	C1v	1m	2
1*	[2,1+]	C1h	1/m ali 21	2
1x	[2+,2+]	S2	21 ali 1	2
11	[ ]+	C1	1	1

Evklidska ravnina

Glavni članek: Seznam grup ravninske simetrije.

Frizijske grupe

Frizijske grupe

notacije				opis	zgledi
IUC	orbifold	Coxeter	Schönflies*
p1	∞∞	[∞,1]+	C∞	Samo translacije. Ta grupa se generira posamezno, z generatorjem, ki je najmanjša razdalja v kateri se vzorec še ponavlja. Abstraktna grupa: Z, grupa celih števil pod seštevanjem.
p11g	∞x	[∞+,2+]	S∞	Drsenje-zrcaljenje in translacije. Ta grupa se generira z drsnim zrcaljenjem skupaj s translacijami, ki so kombinacije dveh drsnih zrcaljenj. Abstraktna grupa: Z
p11m	∞*	[∞+,2]	C∞h	Translacije v horizontalni smeri in drsno zrcaljenje. Ta grupa se generira s translacijo in zrcaljenjem v horizontalni osi. Abstraktna grupa: Z × Z2
p1m1	*∞∞	[∞,1]	C∞v	Translacije in zrcaljenje vzdolž vertikalnih črt. Ta grupa je ista kot netrivialna grupa v enorazsežnem primeru.Generirana je s translacijo in zrcaljenjem v vertikalni osi. Elementi v tej grupi odgovarjajo izometrijam (ali enakovredno bijektivnim afinim transformacijam) množice celih števil in je tako izomorfna množici polneposrednih produktov s celimi števili z Z2. Abstraktna grupa: Dih∞, neskončna diedrska grupa.
p2	22∞	[∞,2]+	D∞	Translacije in vrtenja za 180°. Grupa se generira s translacijo in vrtenjem za 180° . Abstraktna grupa: Dih∞
p2mg	2*∞	[∞,2+]	D∞d	Zrcaljenje preko določenih vertikalnih črt, drsno zrcaljenje, translacije in vrtenja. Translacije v tem primeru nastanejo z drsnim zrcaljenjem. Ta grupa se generira z drsnim zrcaljenjem ali vrtenjem ali vertikalnim zrcaljenjem. Abstraktna grupa: Dih∞
p2mm	*22∞	[∞,2]	D∞h	Translacije, drsno zarcaljenje, zrcaljenje v obeh oseh in vrtenja za 180°. Ta grupa je "največja" frizijska grupa in potrebuje tri generatorje z eno skupino generatojev, ki so sestavljeni iz translacije in zrcaljenja v horizontalni osi in zrcaljenja preko vertikalne osi. Abstraktna grupa: Dih∞ × Z2
*Schönfliesova notacija točkovne grupe je tukaj razširjena kot neskončni primer ekvivalenta diedrskih točkovnih simetrij.

Tapetne grupe

simetrija 632

17 tapetnih grup^[2]

oznaka orbifold	Coxeter	Hermann–Mauguin	Speiser Niggli	Polya Guggenhein	Fejes Toth Cadwell
*632	[6,3]	p6m	C(I)6v	D6	W16
632	[6,3]+	p6	C(I)6	C6	W6
*442	[4,4]	p4m	C(I)4	D*4	W14
4*2	[4+,4]	p4g	CII4v	Do4	W24
442	[4,4]+	p4	C(I)4	C4	W4
*333	[3[3]]	p3m1	CII3v	D*3	W13
3*3	[6,3+]	p31m	CI3v	Do4	W23
333	[3[3]]+	p3	CI3	C3	W3
*2222	[∞,2,∞]	pmm	CI2v	D2kkkk	W22
2*22	[∞,2+,∞]	cmm	CIV2v	D2kgkg	W12
22*	[(∞,2)+,∞]	pmg	CIII2v	D2kkgg	W32
22x	[∞+,2+,∞+]	pgg	CII2v	D2gggg	W42
2222	[∞,2,∞]+	p2	C(I)2	C2	W2
**	[∞,2,∞+]	pm	CIs	D1kk	W21
*x	[∞,2+,∞+]	cm	CIIIs	D1kg	W11
xx	[(∞,2)+,∞+]	pg	CII2	D1gg	W31
o	[∞+,2,∞+]	p1	C(I)1	C1	W1

Hiperbolična ravnina

simetrija 732

Prvih nekaj hiperboličnih grup, urejenih po njihovih orbifold značilnostih je:

Hiperbolične simetrijske grupe^[3]

(-1/znak)	orbifold	Coxeter
(84)	*237	[7,3]
(48)	*238	[8,3]
(42)	237	[7,3]+
(40)	*245	[5,4]
(24)	*2.3.12, *246, *334, 3*4, 238	[12,3], [6,4], [(4,3,3)], [3+,8], [8,3]+
(20)	*2.3.15, *255, 5*2, 245	[15,3], [5,5], [5+,4], [5,4]+
(18+2/3)	*247	[7,4]
(18)	*2.3.18, 239	[18,3], [9,3]+
(16)	*2.3.24, *248	[24,3], [8,4]
(15)	*2.3.30, *256, *335, 3*5, 2.3.10	[30,3], [6,5], [(5,3,3)], [3+,10], [10,3]+
(14+2/5)	*2.3.36, *249	[36,3], [9,4]
(13+1/3)	*2.3.60, *2.4.10	[60,3], [10,4]
(13+1/5)	*2.3.66, 2.3.11	[66,3], [11,3]+
(12+8/11)	*2.3.105, *257	[105,3], [7,5]
(12+4/7)	*2.3.132, *2.4.11 ... *23∞, *2.4.12, *266, 6*2	[132,3], [11,4], ..., [∞,3], [12,4], [6,6], [6+,4]
(12)	*336, 3*6, *344, 4*3, *2223, 2*23, 2.3.12, 246, 334	[(6,3,3)], [3+,12], [(4,4,3)], [4+,6], ... [12,3]+, [6,4]+ [(4,3,3)]+
...