Elipsi

Në matematikë, një elips është një kurbë e rrafshët që rrethon dy pika vatrore, i tillë që për të gjitha pikat në kurbë, shuma e dy distancave me pikat vatrore është një konstante. Elipsi është përgjithësimi i një rrethi, i cili është lloj i veçantë i elipsit në të cilin dy vatrat janë të njëjta. Zgjatja e një elipsi matet me jashtëqendërsinë ${\displaystyle e}$, një numër që varion nga ${\displaystyle e=0}$ ( rasti kufizues i një rrethi) në ${\displaystyle e=1}$ (rasti kufizues i zgjatjes së pafundme, jo më një elips, por një parabolë ).

Një elips (e kuqe) i marrë si kryqëzim i një koni me një plan të pjerrët.

Elipsi: shënimevertex - kulmi , focus - vatra, center - qendra,semi-minor axis - gjysëmboshti i vogël, semi-major axis - gjysëmboshti i madh

Elipsat: shembuj me jashtëqendërsi në rritje

Një elips ka një zgjidhje të thjeshtë algjebrike për sipërfaqjen e tij dhe një pjese të tij, por vetëm përafërsi për perimetrin e tij, për të cilin kërkohet integrim numerik për të marrë një zgjidhje të saktë.

Në mënyrë analitike, ekuacioni i një elipsi standard të përqendruar në origjinë me gjerësi ${\displaystyle 2a}$ dhe lartësi ${\displaystyle 2b}$ është:

${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1.}$

Duke supozuar ${\displaystyle a\geq b}$, vatrat janë ${\displaystyle (\pm c,0)}$ për ${\textstyle c={\sqrt {a^{2}-b^{2}}}}$ . Ekuacioni standard parametrik është:

${\displaystyle (x,y)=(a\cos(t),b\sin(t))\quad {\text{për}}\quad 0\leq t\leq 2\pi .}$

Elipsi është lloji i mbyllur i prerjeve konike : një kurbë e rrafshit që gjurmon prerjen e një koni me një plan (shih figurën). Elipsat kanë shumë ngjashmëri me dy format e tjera të seksioneve konike, parabolat dhe hiperbolat, të cilat të dyja janë të hapura dhe të pakufizuara . Një prerje e tërthortë i pjerrët i një cilindri është gjithashtu një elips.

Elipsat janë të zakonshme në fizikë, astronomi dhe inxhinieri . Për shembull, orbita e secilit planet në Sistemin Diellor është përafërsisht një elips me Diellin në një pikë vatrore. E njëjta gjë vlen dhe për hënat që rrotullohen rreth planeteve dhe të gjitha sistemet e tjera të dy trupave astronomikë. Format e planetëve dhe yjeve shpesh përshkruhen mirë nga elipsoidët . Një rreth i parë nga një kënd anësor duket si një elips.

Emri, ἔλλειψις (élleipsis, "heqje") , u dha nga Apollonius i Pergës në veprën e tij Koniket.

Përkufizimi si një lokus pikash

Elipsi: përcaktimi nga shuma e distancave vatrore

Elipsi: përcaktimi nga fokusi dhe vija drejtuese rrethore

Një elips mund të përkufizohet gjeometrikisht si një grup ose vendndodhje pikash në rrafshin Euklidian:

Jepen dy pika fikse ${\displaystyle F_{1},F_{2}}$ të quajtura vatra dhe një distancë ${\displaystyle 2a}$ e cila është më e madhe se largësia ndërmjet vatrave, elipsa është bashkësia e pikave ${\displaystyle P}$ të tillë që shuma e largësive ${\displaystyle |PF_{1}|,\ |PF_{2}|}$ është e barabartë me ${\displaystyle 2a}$ : ${\displaystyle E=\left\{P\in \mathbb {R} ^{2}\,\mid \,|PF_{2}|+|PF_{1}|=2a\right\}\ .}$

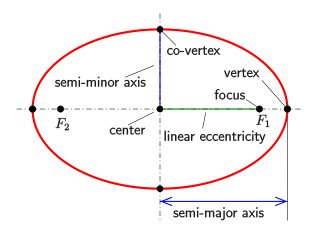
Pika e mesit ${\displaystyle C}$ e segmentit që bashkon vatra quhet qendra e elipsit. Vija që kalon nëpër vatra quhet boshti kryesor, dhe vija pingul me të përmes qendrës është boshti i vogël . Boshti kryesor takon elipsin në dy kulme ${\displaystyle V_{1},V_{2}}$, të cilët kanë distancë ${\displaystyle a}$ në qendër. Distanca ${\displaystyle c}$ e vatrave në qendër quhet distanca vatrore ose jashtëqendërsi lineare. Herësi ${\displaystyle e={\tfrac {c}{a}}}$ është jashtëqendërsia .

Rasti ${\displaystyle F_{1}=F_{2}}$ jep një rreth dhe përfshihet si një lloj i veçantë elipsi.

Në koordinatat karteziane

Parametrat e formës:a: gjysëmboshti i madhb: gjysëmboshti i vogël c: jashtëqendërsia linearep: parametër

Ekuacioni standard

Forma standarde e një elipsi në koordinata karteziane supozon se origjina është qendra e elipsit, boshti x është boshti kryesor dhe:

vatrat janë pikat ${\displaystyle F_{1}=(c,\,0),\ F_{2}=(-c,\,0)}$ ,

kulmet janë ${\displaystyle V_{1}=(a,\,0),\ V_{2}=(-a,\,0)}$ .

Për një pikë arbitrare ${\displaystyle (x,y)}$ largësia nga vatra ${\displaystyle F_{1}}$ është ${\textstyle {\sqrt {(x-c)^{2}+y^{2}}}}$ dhe nga vatra ${\displaystyle F_{2}}$ ${\textstyle {\sqrt {(x+c)^{2}+y^{2}}}}$ . Prandaj pika ${\displaystyle (x,\,y)}$ është në vijë për:

${\displaystyle {\sqrt {(x-c)^{2}+y^{2}}}+{\sqrt {(x+c)^{2}+y^{2}}}=2a\ .}$

Duke përdorur ${\displaystyle b^{2}=a^{2}-c^{2}}$ marrim ekuacionin standard i cili jepet nga formula:

${\displaystyle y=\pm {\frac {b}{a}}{\sqrt {a^{2}-x^{2}}}=\pm {\sqrt {\left(a^{2}-x^{2}\right)\left(1-e^{2}\right)}}.}$

Një drejtëz e çfarëdoshme ${\displaystyle g}$ e pret një elipsë në 0, 1 ose 2 pika, përkatësisht të quajtura vijë e jashtme, tangjente dhe sekante . Përmes çdo pike të një elipsi ka një tangjente unike. Tangjentja në një pikë ${\displaystyle (x_{1},\,y_{1})}$ të elipsit ${\displaystyle {\tfrac {x^{2}}{a^{2}}}+{\tfrac {y^{2}}{b^{2}}}=1}$ ka ekuacionin e koordinatave:

Akset kryesore

Jashtëqendërsia lineare

Kjo është largësia nga qendra në një fokus: ${\displaystyle c={\sqrt {a^{2}-b^{2}}}}$ .

Tangjentja

Një vijë e çfarëdoshme ${\displaystyle g}$ e pret një elipsë në 0, 1 ose 2 pika, përkatësisht të quajtura vijë e jashtme, tangjente dhe sekante . Përmes çdo pike të një elipsi ka një tangjente unike. Tangjentja në një pikë ${\displaystyle (x_{1},\,y_{1})}$ të elipsit ${\displaystyle {\tfrac {x^{2}}{a^{2}}}+{\tfrac {y^{2}}{b^{2}}}=1}$ ka ekuacionin e koordinatave:Stampa:NumBlk${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1}$

${\displaystyle (x,\,y)=(a\cos t,\,b\sin t),\ 0\leq t<2\pi \ .}$

Duke përdorur funksionet trigonometrike, një paraqitje parametrike e elipsit standard ${\displaystyle {\tfrac {x^{2}}{a^{2}}}+{\tfrac {y^{2}}{b^{2}}}=1}$ është:

${\displaystyle r(\theta )={\frac {ab}{\sqrt {(b\cos \theta )^{2}+(a\sin \theta )^{2}}}}={\frac {b}{\sqrt {1-(e\cos \theta )^{2}}}}}$

Elipsi i zhvendosur

Nëse elipsi standard zhvendoset në qendër ${\displaystyle \left(x_{\circ },\,y_{\circ }\right)}$, ekuacioni i tij është:

${\displaystyle {\frac {\left(x-x_{\circ }\right)^{2}}{a^{2}}}+{\frac {\left(y-y_{\circ }\right)^{2}}{b^{2}}}=1\ .}$

Paraqitja parametrike

Ndërtimi i pikave bazuar në ekuacionin parametrik dhe interpretimi i parametrit t

Paraqitja standarde parametrike

Duke përdorur funksionet trigonometrike, një paraqitje parametrike e elipsit standard ${\displaystyle {\tfrac {x^{2}}{a^{2}}}+{\tfrac {y^{2}}{b^{2}}}=1}$ është:

${\displaystyle (x,\,y)=(a\cos t,\,b\sin t),\ 0\leq t<2\pi \ .}$

Parametri t (i quajtur anomali jashtëqendërsie në astronomi) nuk është këndi i ${\displaystyle (x(t),y(t))}$ me boshtin oX, por ka një kuptim gjeometrik të dhënë nga Philippe de La Hire (shih Vizatimi i elipseve më poshtë). ^[1]

Forma polare

Koordinatat polare të përqendruara në qendër.

Në koordinatat polare, me origjinë në qendrën e elipsit dhe me koordinatë këndore ${\displaystyle \theta }$ e matur nga boshti kryesor, ekuacioni i elipsit është ^{[2] :p. 75}

${\displaystyle C\,=\,4a\int _{0}^{\pi /2}{\sqrt {1-e^{2}\sin ^{2}\theta }}\ d\theta \,=\,4a\,E(e)}$

Veti të matjes

Të gjitha vetitë metrike të dhëna më poshtë i referohen një elipsi me ekuacion

Sipërfaqja

Sipërfaqja ${\displaystyle S_{\text{elips}}}$ e mbyllur nga një elips është:Stampa:NumBlk${\displaystyle S_{elips}=\pi ab}$

ku ${\displaystyle a}$ dhe ${\displaystyle b}$ janë përkatësisht gjatësitë e gjysëmboshtit të madh dhe gjysëmboshtit të vogël. Formula e sipërfaqes ${\displaystyle \pi ab}$ është intuitive: filloni me një rreth me rreze ${\displaystyle b}$ (kështu është sipërfaqja e saj ${\displaystyle \pi b^{2}}$ ) dhe e shtrini atë me një faktor ${\displaystyle a/b}$ për të bërë një elips. Kjo shkallëzon zonën me të njëjtin faktor: ${\displaystyle \pi b^{2}(a/b)=\pi ab.}$ ^[3] Megjithatë, përdorimi i së njëjtës qasje për perimetrin do të ishte i gabuar - krahasoni integralet ${\textstyle \int f(x)\,dx}$ dhe ${\textstyle \int {\sqrt {1+f'^{2}(x)}}\,dx}$ . Është gjithashtu e lehtë të vërtetohet me rigorozitet formula e zonës duke përdorur integrimin.

${\displaystyle S_{\text{elips}}={\frac {b}{a}}\pi a^{2}=\pi ab.}$

Integrali i dytë është zona e një rrethi me rreze ${\displaystyle a,}$ kjo eshte, ${\displaystyle \pi a^{2}.}$ Kështu që

Zona e mbyllur nga një elips i anuar është ${\displaystyle \pi \;y_{\text{int}}\,x_{\text{max}}}$ .

Deri më tani kemi trajtuar elipsë të ngritur, boshtet kryesore dhe të vogla të të cilëve janë paralele me ${\displaystyle x}$ dhe ${\displaystyle y}$ sëpata. Megjithatë, disa zbatime kërkojnë elipsë të pjerrët. Në optikën e rrezeve me grimca të ngarkuara, për shembull, zona e mbyllur e një elipsi të ngritur ose të pjerrët është një veti e rëndësishme e rrezes, emetimi i saj. Në këtë rast ende zbatohet një formulë e thjeshtë, domethënë

${\displaystyle S_{elips}=\pi \;y_{int}\;x_{max}=\pi \;x_{int}\;y_{max}}$

ku ${\displaystyle y_{\text{int}}}$, ${\displaystyle x_{\text{int}}}$ janë përgjimet dhe ${\displaystyle x_{\text{max}}}$, ${\displaystyle y_{\text{max}}}$ janë vlerat maksimale. Ky përfundim rrjedh drejtpërdrejt nga teorema e Apollonit .

Perimetri

Elipsë me perimetër të njëjtë

Perimetri ${\displaystyle C}$ i një elipsi është:

${\displaystyle C=4a\int \limits _{0}^{\frac {\pi }{2}}{\sqrt {1-e^{2}sin^{2}\theta }}d\theta =4aE(e)}$

Ky integral është eliptik i llojit të dytë dhe përgjithësisht nuk paraqitet me anë të funksioneve elementare.

Srinivasa Ramanujan dha dy përafrime të afërta për perimetrin në §16 të "Ekuacionet modulare dhe përafrimet në ${\displaystyle \pi }$ "; ^[4] ata janë:

${\displaystyle C\approx \pi [3(a+b)-{\sqrt {(3a+b)(a+3b)}}]}$

Gjatësia e harkut

Në përgjithësi, gjatësia e harkut të një pjese të perimetrit, si funksion i këndit të tendosur (ose abshisat e çdo dy pikave në gjysmën e sipërme të elipsit), jepen nga një integral eliptik jo i plotë. Gjysma e sipërme e një elipsi parametrizohet nga

${\displaystyle y=b\ {\sqrt {1-{\frac {x^{2}}{a^{2}}}\ }}~.}$

Pastaj gjatësia e harkut ${\displaystyle s}$ nga ${\displaystyle x_{1}}$ te ${\displaystyle x_{2}}$ është:

${\displaystyle s=-b\int _{\arccos {\frac {x_{1}}{a}}}^{\arccos {\frac {x_{2}}{a}}}{\sqrt {\ 1+\left({\tfrac {a^{2}}{b^{2}}}-1\right)\ \sin ^{2}z~}}\;\mathrm {d} z~.}$

Kjo është e barabartë me

${\displaystyle s=b\ \left[\;E\left(z\;{\Biggl |}\;1-{\frac {a^{2}}{b^{2}}}\right)\;\right]_{z\ =\ \arccos {\frac {x_{2}}{a}}}^{\arccos {\frac {x_{1}}{a}}}}$

ku ${\displaystyle E(z\mid m)}$ është integrali eliptik jo i plotë i llojit të dytë me parametër ${\displaystyle m=k^{2}.}$

Si seksione të rrafshët të kuadrikëve

Elipsat shfaqen si prerje të rrafshta të kuadrikëve të mëposhtëm:

• Elipsoid
• Kon eliptik
• Cilindri eliptik
• Hiperboloid me një napë
• Hiperboloid me dy napa

• 
  Elipsoid
• 
  Kon eliptik
• 
  Cilindri eliptik
• 
  Hiperboloid me një napë
• 
  Hiperboloidi me dy napa

Aplikacionet

Reflektorët eliptikë dhe akustika

Modeli i valës së një pikëze të vogël të rënë në merkur në njërën vatër të elipsit

Nëse sipërfaqja e ujit ngacmohet në një nga vatrat e një rezervuari uji eliptik, valët rrethore të këtij ngacmimi, pasi reflektohen nga muret, konvergjojnë njëkohësisht në një pikë të vetme: vatrën e dytë . Kjo është pasojë e gjatësisë totale të udhëtimit që është e njëjtë përgjatë çdo shtegu reflektimi midis dy vatrave.

Në mënyrë të ngjashme, nëse një burim drite vendoset në një vatër të një pasqyre eliptike, të gjitha rrezet e dritës në rrafshin e elipsit reflektohen në vatrën e dytë. Meqenëse asnjë kurbë tjetër e lëmuar nuk ka një veti të tillë, ajo mund të përdoret si një përkufizim alternativ i një elipsi. (Në rastin e veçantë të një rrethi me një burim në qendër, e gjithë drita do të reflektohej përsëri në qendër. ) Nëse elipsi rrotullohet përgjatë boshtit të tij kryesor për të prodhuar një pasqyrë elipsoidale, kjo veti vlen për të gjitha rrezet jashtë burimit. Përndryshe, një pasqyrë cilindrike me prerje tërthore eliptike mund të përdoret për të fokusuar dritën nga një llambë fluoreshente lineare përgjatë një vije letre; pasqyra të tilla përdoren në disa skanera dokumentesh .

Orbitat planetare

Në shekullin e 17-të, Johannes Kepleri zbuloi se orbitat përgjatë të cilave planetët udhëtojnë rreth Diellit janë elipsa me Diellin [përafërsisht] në një vatër, në ligjin e tij të parë të lëvizjes planetare . Më vonë, Isak Njutoni e shpjegoi këtë si rrjedhojë e ligjit të tij të gravitetit universal .

Në përgjithësi, në problemin e rëndesës me dy trupa, nëse të dy trupat janë të lidhur me njëri-tjetrin (d.m.th., energjia totale është negative), orbitat e tyre janë elipsa të ngjashëm me bariqendrën e përbashkët që është një nga vatrat e çdo elipsi. Vatra tjetër i secilit elips nuk ka asnjë domethënie fizike të njohur. Orbita e secilit trup në kuadrin e referencës së tjetrit është gjithashtu një elips, me trupin tjetër në të njëjtën vatër.

Orbitat eliptike Kepleriane janë rezultat i çdo force tërheqëse të drejtuar sipas rrezes (rrezore). Forca është në përpjesëtim të zhdrejtë me katrorin e largësisë. Kështu, në parim, lëvizja e dy grimcave të ngarkuara në mënyrë të kundërt në hapësirën boshe do të ishte gjithashtu një elips. (Megjithatë, ky përfundim injoron humbjet për shkak të rrezatimit elektromagnetik dhe efekteve kuantike, të cilat bëhen të rëndësishme kur grimcat lëvizin me shpejtësi të madhe. )

Për orbitat eliptike, marrëdhëniet e dobishme që përfshijnë jashtëqendërsinë ${\displaystyle e}$ janë:

${\displaystyle {\begin{aligned}a&={\frac {r_{a}+r_{p}}{2}}\\[2pt]b&={\sqrt {r_{a}r_{p}}}\\[2pt]\ell &={\frac {2}{{\frac {1}{r_{a}}}+{\frac {1}{r_{p}}}}}={\frac {2r_{a}r_{p}}{r_{a}+r_{p}}}\end{aligned}}}$ .

• ${\displaystyle r_{a}}$ është rrezja në apoaps (largësia më e largët)
• ${\displaystyle r_{p}}$ është rrezja në periaps (largësia më e afërt)
• ${\displaystyle a}$ është gjatësia e gjysëmboshtit të madh

Gjithashtu, për sa i përket ${\displaystyle r_{a}}$ dhe ${\displaystyle r_{p}}$, gjysëmboshti i madh ${\displaystyle a}$ është mesatarja e tyre aritmetike, boshti gjysmë i vogël ${\displaystyle b}$ është mesatarja e tyre gjeometrike dhe parametri ${\displaystyle \ell }$ është mesatarja e tyre harmonike . Me fjale te tjera,

Lëkundësit harmonikë

Zgjidhja e përgjithshme për një lëkundësi harmonik në dy ose më shumë dimensione është gjithashtu një elips. I tillë është rasti, për shembull, i një lavjerrësi të gjatë që lëviz në dy dimensione; i një mase të ngjitur në një pikë fikse nga një sustë krejtësisht elastike; ose i çdo objekti që lëviz nën ndikimin e një force tërheqëse që është drejtpërdrejt e përpjesshme me largësinë e tij nga një tërheqës fiks. Megjithatë, ndryshe nga orbitat Kepleriane, këto "orbita harmonike" kanë qendrën e tërheqjes në qendrën gjeometrike të elipsit dhe kanë ekuacione mjaft të thjeshta të lëvizjes.

Vizualizimi i fazës

Në elektronikë, faza relative e dy sinjaleve sinusoidale mund të krahasohet duke i ushqyer ato në hyrjet vertikale dhe horizontale të një oshiloskopi . Nëse shfaqja e figurës Lissajous është një elips, dhe jo një vijë e drejtë, të dy sinjalet janë jashtë fazës.

Ingranazhet eliptike

Dy ingranazhe jo rrethore me të njëjtin skicë eliptike, secila duke u rrotulluar rreth një vatre dhe të pozicionuara në këndin e duhur, rrotullohen pa probleme duke ruajtur kontaktin gjatë gjithë kohës. Përndryshe, ato mund të lidhen me një zinxhir lidhës ose rrip kohues, ose në rastin e një biçiklete unaza kryesore e zinxhirit mund të jetë eliptike ose një vezake e ngjashme me një elips në formë. Ingranazhe të tilla eliptike mund të përdoren në pajisjet mekanike për të prodhuar shpejtësi këndore ose çift rrotullues të ndryshueshëm nga një rrotullim konstant i boshtit lëvizës, ose në rastin e një biçiklete për të lejuar një shpejtësi të ndryshme rrotullimi të manivelit me përparësi mekanike të ndryshueshme.

Ingranazhet eliptike të biçikletave e bëjnë më të lehtë që zinxhiri të rrëshqasë nga dhëmbëzimi kur ndërron marshin. ^[5]

Një shembull i zbatimit të ingranazheve do të ishte një pajisje që mbështjell fijen mbi një bobine konike në një makinë tjerrëse . Bobina do të duhet të mbështillet më shpejt kur filli është afër majës sesa kur është afër bazës. ^[6]

Optika

• Në burimet e dritës EUV të prodhuara nga plazma lazer të përdorura në litografinë me mikroçip, drita EUV gjenerohet nga plazma e pozicionuar në fokusin parësor të një pasqyre elipsoidale dhe mblidhet në fokusin dytësor në hyrjen e makinës së litografisë. ^[7]

Statistika dhe financa

Në statistikë, një vektor i rastësishëm bivariant ${\displaystyle (X,Y)}$ ka shpërndarje të dyfishtë eliptike nëse konturet e tij me izo-densitet - lokacione me vlera të barabarta të funksionit të densitetit - janë elipse. Koncepti shtrihet në një numër arbitrar të elementeve të vektorit të rastësishëm, në të cilin rast në përgjithësi konturet e izo-densitetit janë elipsoidë. Një rast i veçantë është shpërndarja normale multivariate . Shpërndarjet eliptike janë të rëndësishme në financë sepse nëse normat e kthimit të aktiveve shpërndahen bashkërisht në mënyrë eliptike, atëherë të gjitha portofolet mund të karakterizohen plotësisht nga mesatarja dhe varianca e tyre - domethënë, çdo dy portofole me pritje dhe variancë të njëjtë të kthimit të portofolit kanë shpërndarje identike kthimi të portofolit. ^{[8] [9]}

Teoria e optimizmit

Ndonjëherë është e dobishme të gjesh elipsin kufizues minimal të një grup pikash. Metoda elipsoide është mjaft e dobishme për zgjidhjen e këtij problemi.

1. K. Strubecker: Vorlesungen über Darstellende Geometrie, GÖTTINGEN, VANDENHOECK & RUPRECHT, 1967, p. 26
2. Lawrence, J. Dennis, A Catalog of Special Plane Curves, Dover Publ., 1972.
3. Archimedes. (1897). The works of Archimedes. Heath, Thomas Little, Sir, 1861-1940. Mineola, N.Y.: Dover Publications. fq. 115. ISBN 0-486-42084-1. OCLC 48876646. {{cite book}}: Mungon ose është bosh parametri |language= (Ndihmë!)
4. Ramanujan, Srinivasa (1914). "Modular Equations and Approximations to π". Quart. J. Pure App. Math. 45: 350–372. ISBN 9780821820766. {{cite journal}}: Mungon ose është bosh parametri |language= (Ndihmë!)
5. David Drew. "Elliptical Gears".
6. Grant, George B. (1906). A treatise on gear wheels. Philadelphia Gear Works. fq. 72. {{cite book}}: Mungon ose është bosh parametri |language= (Ndihmë!)
7. "Cymer - EUV Plasma Chamber Detail Category Home Page". Arkivuar nga origjinali më 2013-05-17. Marrë më 2013-06-20. {{cite web}}: Mungon ose është bosh parametri |language= (Ndihmë!)
8. Chamberlain, G. (shkurt 1983). "A characterization of the distributions that imply mean—Variance utility functions". Journal of Economic Theory. 29 (1): 185–201. doi:10.1016/0022-0531(83)90129-1. {{cite journal}}: Mungon ose është bosh parametri |language= (Ndihmë!)
9. Owen, J.; Rabinovitch, R. (qershor 1983). "On the class of elliptical distributions and their applications to the theory of portfolio choice". Journal of Finance. 38 (3): 745–752. doi:10.1111/j.1540-6261.1983.tb02499.x. JSTOR 2328079. {{cite journal}}: Mungon ose është bosh parametri |language= (Ndihmë!)