Функција грешке

У математици, функција грешке (такође позната и као Гаусова функција грешке) је неелементарна функција која се јавља у вероватноћи, статистици, и парцијалним диференцијалним једначинама.

График функције грешке

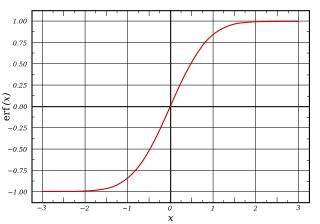
Дефинише се као:

${\displaystyle \operatorname {erf} (x)={\frac {2}{\sqrt {\pi }}}\int _{0}^{x}e^{-t^{2}}\,\mathrm {d} t.}$

Комплементарна функција грешке, која се означава као , је дефинисана преко функције грешке:

${\displaystyle {\mbox{erfc}}(x)=1\mbox{erf}}(x)={\frac {2}{\sqrt {\pi }}}\int _{x}^{\infty }e^{-t^{2}}\,\mathrm {d} t.}$

Комплексна функција грешке, означена као w(x), (позната и као Фадеева функција) је такође дефинисана преко функције грешке:

${\displaystyle w(x)=e^{-x^{2}}{\textrm {erfc}}(-ix).\,\!}$

Својства

Функција грешке је непарна функција:

${\displaystyle \operatorname {erf} (-x)=-\operatorname {erf} (x).}$

За сваки комплексан број x важи

${\displaystyle \operatorname {erf} ({\overline {x}})={\overline {\operatorname {erf} (x)}}}$

где је ${\displaystyle {\overline {x}}}$ конјуговано комплексна вредност ${\displaystyle x}$.

Интеграл се не може израчунати у затвореној форми елементарних функција, али развојем подинтегралног дела у Тејлоров ред, добија се Тејлоров ред функције грешке као:

${\displaystyle \operatorname {erf} (x)={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n+1}}{n!(2n+1)}}={\frac {2}{\sqrt {\pi }}}\left(x\frac {x^{3}}{3}}+{\frac {x^{5}}{10}{\frac {x^{7}}{42}}+{\frac {x^{9}}{216}}-\ \cdots \right)}$

који важи за сваки реалан број ${\displaystyle x}$, и такође за целу комплексну раван. (Ово произилази из развоја Тејлоровог реда ${\displaystyle e^{-x^{2}}}$, што је ${\displaystyle \sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n}}{n!}}}$, који потом интегралимо члан по члан.)

За итеративно израчунавање горњег реда, следећа алтернативна формулација може бити од користи:

${\displaystyle \operatorname {erf} (x)={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }\left(x\prod _{i=1}^{n}{\frac {-(2i-1)x^{2}}{i(2i+1)}}\right)={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }{\frac {x}{2n+1}}\prod _{i=1}^{n}{\frac {-x^{2}}{i}}}$

јер ${\displaystyle {\frac {-(2i-1)x^{2}}{i(2i+1)}}}$ претвара чинилац из ${\displaystyle i}$-тог члана у ${\displaystyle (i+1)}$. члан (под претпоставком да први члан означавамо као ${\displaystyle x}$).

Функција грешке у бесконачности има вредност 1 (погледати Гаусов интеграл).

Извод функције грешке следи директно из њене дефиниције:

${\displaystyle {\frac {d}{dx}}\,\mathrm {erf} (x)={\frac {2}{\sqrt {\pi }}}\,e^{-x^{2}}.}$

Инверзна функција грешке има ред

${\displaystyle \operatorname {erf} ^{-1}(x)=\sum _{k=0}^{\infty }{\frac {c_{k}}{2k+1}}\left({\frac {\sqrt {\pi }}{2}}x\right)^{2k+1},\,\!}$

где је , а

${\displaystyle c_{k}=\sum _{m=0}^{k-1}{\frac {c_{m}c_{k-1-m}}{(m+1)(2m+1)}}=\left\{1,1,{\frac {7}{6}},{\frac {127}{90}},\ldots \right\}.}$

Тако добијамо развој реда (приметити да су поништени заједнички чиниоци из имениоца и бројиоца):

${\displaystyle \operatorname {erf} ^{-1}(x)={\frac {1}{2}}{\sqrt {\pi }}\left(x+{\frac {\pi x^{3}}{12}}+{\frac {7\pi ^{2}x^{5}}{480}}+{\frac {127\pi ^{3}x^{7}}{40320}}+{\frac {4369\pi ^{4}x^{9}}{5806080}}+{\frac {34807\pi ^{5}x^{11}}{182476800}}+\cdots \right).\,\!}$

Вредност функције грешке у ${\displaystyle \pm \infty }$ је једнака ${\displaystyle \pm 1}$.

Примене

Када се резултати више мерења опишу нормалном расподелом са стандардном девијацијом ${\displaystyle \sigma }$ и очекиваном вредношћу 0, онда је ${\displaystyle \operatorname {erf} \,\left(\,{\frac {a}{\sigma {\sqrt {2}}}}\,\right)}$ вероватноћа да грешка једног мерења лежи између ${\displaystyle -a}$ и ${\displaystyle +a}$.

У дигиталним оптичким телекомуникацијама, однос бит-грешка се изражава као:

${\displaystyle \mathrm {BER} =0.5\,\operatorname {erf} \left({\frac {\mu _{1}-\mu _{2}}{{\sqrt {2}}\left(\sigma _{1}+\sigma _{2}\right)}}\right).}$

Асимптототски развој

Корисни асимптотски развој комплементарне функције грешке (а самим тим и функције грешке) за велико x је

${\displaystyle \mathrm {erfc} (x)={\frac {e^{-x^{2}}}{x{\sqrt {\pi }}}}\left[1+\sum _{n=1}^{\infty }(-1)^{n}{\frac {1\cdot 3\cdot 5\cdots (2n-1)}{(2x^{2})^{n}}}\right]={\frac {e^{-x^{2}}}{x{\sqrt {\pi }}}}\sum _{n=0}^{\infty }(-1)^{n}{\frac {(2n)!}{n!(2x)^{2n}}}.\,}$

Овај ред дивергира за свако коначно x. Практично, само првих пар чланова овог развоја је потребно да се израчуна добра апроксимација , док Тејлоров ред дат изнад конвергира јако споро.

Још једна апроксимација је дата са

${\displaystyle (\operatorname {erf} (x))^{2}\approx 1-\exp \left(-x^{2}{\frac {4/\pi +ax^{2}}{1+ax^{2}}}\right)}$

где је

${\displaystyle a={\frac {-8}{3\pi }}{\frac {\pi -3}{\pi -4}}.}$

Сродне функције

Функција грешке је суштински идентична стандардној нормалној кумулативној функцији расподеле, означеној као Φ, јер се оне разликују само по скалирању и транслацији:

${\displaystyle \Phi (x)={\frac {1}{2}}\left[1+{\mbox{erf}}\left({\frac {x}{\sqrt {2}}}\right)\right]\,.}$

Генерализована функција грешке

График генерализоване функције грешке ${\textstyle E_{1}(x)}$:
сива крива: ${\textstyle E_{1}(x)=(1-e^{-x})/{\sqrt {\pi }}}$
црвена крива: ${\textstyle E_{2}(x)=\operatorname {erf} (x)}$
зелена крива: ${\textstyle E_{3}(x)}$
плава крива: ${\textstyle E_{4}(x)}$
златна крива: ${\textstyle E_{5}(x)}$.

Неки аутори расправљају о општијој функцији

${\displaystyle E_{n}(x)={\frac {n!}{\sqrt {\pi }}}\int _{0}^{x}e^{-t^{n}}\,\mathrm {d} t={\frac {n!}{\sqrt {\pi }}}\sum _{p=0}^{\infty }(-1)^{p}{\frac {x^{np+1}}{(np+1)p!}}\,.}$

Случајеви вредни помена су:

• E₀(x) је права линија дефинисана као: ${\displaystyle E_{0}(x)={\frac {x}{e{\sqrt {\pi }}}}}$
• E₂(x) је функција грешке, .

После дељења са !, све за непарно изгледају слично (али не и идентично) једна другој. Слично томе, за парно изгледају слично (али не и идентично) једна другој после простог дељења са !. Све генерализоване функције грешке за изгледају слично за позитивне вредности на графику.

Ове генерализоване функције се за x>0 могу еквивалентно представити користећи Гама функцију:

${\displaystyle E_{n}(x)={\frac {x\left(x^{n}\right)^{-1/n}\Gamma (n)\left(\Gamma \left({\frac {1}{n}}\right)-\Gamma \left({\frac {1}{n}},x^{n}\right)\right)}{\sqrt {\pi }}},\quad \quad x>0}$

Према овоме, можемо дефинисати функцију грешке преко Гама функције:

${\displaystyle \operatorname {erf} (x)=1-{\frac {\Gamma \left({\frac {1}{2}},x^{2}\right)}{\sqrt {\pi }}}}$

Итеративни интеграли комплементарне функције грешке

Итеративни интеграли комплементарне функције грешке су дефинисани преко:

${\displaystyle \mathrm {i} ^{n}\operatorname {erfc} \,(z)=\int _{z}^{\infty }\mathrm {i} ^{n-1}\operatorname {erfc} \,(\zeta )\;\mathrm {d} \zeta .\,}$

Оне имају степени ред:

${\displaystyle \mathrm {i} ^{n}\operatorname {erfc} \,(z)=\sum _{j=0}^{\infty }{\frac {(-z)^{j}}{2^{n-j}j!\Gamma \left(1+{\frac {n-j}{2}}\right)}}\,,}$

из кога следе својства симетричности

${\displaystyle \mathrm {i} ^{2m}\operatorname {erfc} (-z)=-\mathrm {i} ^{2m}\operatorname {erfc} \,(z)+\sum _{q=0}^{m}{\frac {z^{2q}}{2^{2(m-q)-1}(2q)!(m-q)!}}}$

и

${\displaystyle \mathrm {i} ^{2m+1}\operatorname {erfc} (-z)=\mathrm {i} ^{2m+1}\operatorname {erfc} \,(z)+\sum _{q=0}^{m}{\frac {z^{2q+1}}{2^{2(m-q)-1}(2q+1)!(m-q)!}}\,.}$

Имплементација

: Имплементирана је као функција и у заглављу или у ГНУ верзији. Ово није део стандарда и зависи од имплементационе библиотеке. Парови функција {erff(),erfcf()} и {erfl(),erfcl()} узимају и враћају типове и .

Види још

• Гаусова функција

Спољашње везе