இசைச் சராசரி

கணிதத்தின் பலவகையான சராசரிகளுள் இசைச் சராசரியும் (harmonic mean) ஒன்று. வீதம் அல்லது விகிதங்களின் சராசரிகள் தேவைப்படும் சூழ்நிலைகளில், இசைச் சராசரி பிற சராசரிகளைவிட மிகவும் பொருத்தமானது.

தரப்பட்ட நேர்ம எண்கள்: x₁, x₂, ..., x_n > 0 எனில்,

இவற்றின் இசைச்சராசரி காணும் வாய்ப்பாடு:

${\displaystyle H={\frac {n}{{\frac {1}{x_{1}}}+{\frac {1}{x_{2}}}+\cdots +{\frac {1}{x_{n}}}}}={\frac {n}{\sum _{i=1}^{n}{\frac {1}{x_{i}}}}}={\frac {n\cdot \prod _{j=1}^{n}x_{j}}{\sum _{i=1}^{n}{\frac {\prod _{j=1}^{n}x_{j}}{x_{i}}}}}.}$

மூன்றாவது வாய்ப்பாட்டிலிருந்து இசைச் சராசரி, கூட்டுச் சராசரி மற்றும் பெருக்கல் சராசரியுடன் தொடர்புள்ளது எனத் தெரிகிறது. ஒரு தரவின் இசைச் சராசரி அத்தரவிலுள்ள உறுப்புகளின் பெருக்கல் தலைகீழிகளின் கூட்டுச் சராசரியின் பெருக்கல் தலைகீழியாகும்.

எடுத்துக்காட்டாக 1, 2, மற்றும் 4 ஆகிய எண்களின் இசைச் சராசரி:

${\displaystyle {\frac {3}{{\frac {1}{1}}+{\frac {1}{2}}+{\frac {1}{4}}}}={\frac {1}{{\frac {1}{3}}({\frac {1}{1}}+{\frac {1}{2}}+{\frac {1}{4}})}}={\frac {12}{7}}\,.}$

பிற சராசரிகளுடனான தொடர்பு

இரு எண்களின் பித்தாகரஸ் சராசரிகள் மூன்றின் வடிவவியல் வ்ரைதல். இசைச் சராசரி H பர்ப்பிள் வண்ணத்தில் காட்டப்பட்டுள்ளது

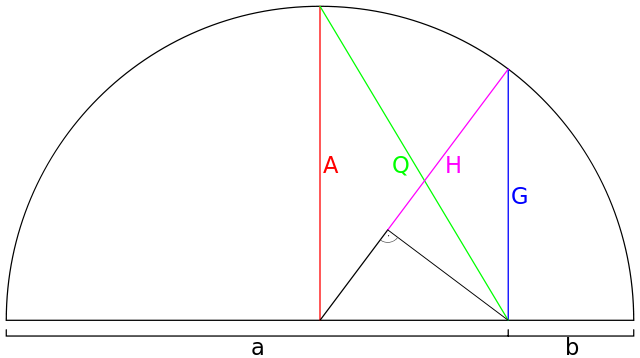
இசைச் சராசரி, பித்தாகரஸ் சராசரிகளுள் ஒன்று. குறைந்தது ஒரு சோடி சமமல்லாத மதிப்புகள் கொண்ட அனைத்து நேர்ம தரவுகளின் கணங்களுக்கு, அவற்றின் கூட்டு, பெருக்கல் மற்றும் இசைச் சராசரி ஆகிய மூன்றில், இசைச் சராசரி சிறியதாகவும் கூட்டுச் சராசரி பெரியதாகவும் பெருக்கல் சராசரி இவ்விரண்டிற்கும் இடைப்பட்டதாகவும் இருக்கும்.

இசைச் சராசரி: ${\displaystyle H}$ ; பெருக்கல் சராசரி: ${\displaystyle G}$ ; கூட்டல் சராசரி: ${\displaystyle A}$ எனில்:

${\displaystyle H<G<A.}$

வெற்றுக் கணமல்லாத ஒரு தரவு கணத்தின் அனைத்து உறுப்புகளும் சமம் என்றால் அத்தரவின் இம்மூன்று சராசரிகளும் சமம்.

${\displaystyle H=G=A.}$

{2, 2, 2} -ஆகியவற்றின் கூட்டு, பெருக்கல் மற்றும் இசைச் சராசரிகள் மூன்றும்  2.

இசைச் சராசரி அடுக்குச் சராசரியின் ஒரு சிறப்பு வகை: M₋₁

சில சமயங்களில் இசைச் சராசரி தேவைப்படும் இடங்களில் தவறுதலாக கூட்டுச் சராசரி பயன்படுத்தப்படுகிறது.^[1] கீழே எடுத்துக்காட்டுகள் பகுதியிலுள்ள வேகம்-எடுத்துக்காட்டில் கூட்டுச் சராசரி 50 மிகவும் பெரியதும் தவறானதுமான ஒரு மதிப்பு.

இசைச் சராசரியின் வாய்ப்பட்டின் மூன்றாவது அமைப்பு, இச்சராசரி மற்ற இரு பித்தாகரஸ் சராசரிகளுடன் கொண்டுள்ள தொடர்பைக் காட்டுகிறது.

வாய்ப்பாட்டின் பகுதியுடன் தொகுதியிலுள்ள n -ஐச் சேர்த்துக் கொள்ள, அது n எண்களின் பெருக்குத்தொகைகளின் கூட்டுச் சராசரியாக அமையும். ஆனால் ஒவ்வொரு j -ஆவதுபெருக்குத்தொகையிலும் n எண்களில் j -ஆவது எண்ணை விட்டுவிட்டு மீதமுள்ள எண்கள் பெருக்கப்படுவதாகக் கொள்ள வேண்டும். அதாவது முதல் பெருக்குத்தொகையில் n எண்களில் முதல் எண்ணை விட்டுவிட்டு மீதமுள்ளவற்றையும் இரண்டாவது பெருக்குத்தொகையில் n எண்களில் இரண்டாவது எண்ணை விட்டுவிட்டு மீதமுள்ளவற்றையும்..... n -ஆவது பெருக்குத்தொகையில் n எண்களில் n -ஆவது எண்ணை விட்டுவிட்டு மீதமுள்ளவற்றையும் பெருக்கிக் கொள்ள வேண்டும்.

வாய்ப்பட்டின் தொகுதி, (பகுதியுடன் சேர்த்து எடுத்துக் கொள்ளப்பட்ட n நீங்கலாக) பெருக்கல் சராசரியின் அடுக்கு n ஆகும்.

இவ்வாறாக n -ஆவது இசைச் சராசரி n -ஆவது பெருக்கல் மற்றும் கூட்டுச் சராசரிகளுடன் தொடர்பு கொண்டுள்ளது.

சமமல்லாத உறுப்புகளைக் கொண்ட தரவு கணத்தில் இரண்டு அல்லது இரண்டுக்கும் மேற்பட்ட உறுப்புகள் பரவியிருக்கும் வீச்சு அதிகமாக இருந்தால் கூட்டுச் சராசரியின் மதிப்புக்குப் பாதிப்பு இருக்காது. ஆனால் இசைச் சராசரியின் மதிப்பு குறைந்துவிடும்.^[2]

எடையிடப்பட்ட இசைச் சராசரி

தரவு கணம்:

${\displaystyle x_{1}}$, ..., ${\displaystyle x_{n}.}$

அவற்றுடன் இணைக்கப்பட்ட எடைகள்:

${\displaystyle w_{1}}$, ..., ${\displaystyle w_{n}}$ எனில்,

இத்தரவின் எடையிடப்பட்ட இசைச் சராசரியின் வாய்ப்பாடு:

${\displaystyle {\frac {\sum _{i=1}^{n}w_{i}}{\sum _{i=1}^{n}{\frac {w_{i}}{x_{i}}}}}.}$

முன்பு வரையறுக்கப்பட்ட சாதாரண இசைச் சராசரி, எடைகள் அனைத்தும் 1 ஆகக் கொண்டுள்ள எடையிடப்பட்ட சராசரி அல்லது அனைத்து எடைகளும் சமமாகவுள்ள எடையிடப்பட்ட இசைச் சராசரியாகும்.

எடுத்துக்காட்டுகள்

இயற்பியலில்

இயற்பியலில் சில இடங்களில், குறிப்பாக வீதங்கள் மற்றும் விகிதங்கள் சம்பந்தப்பட்ட இடங்களில் இசைச் சராசரி மிகவும் பொருத்தமான சராசரியாக இருக்கும்.

• x (60 கி.மீ./மணி) வேகத்தில் ஒரு குறிப்பிட்ட தூரத்தைக் கடக்கும் ஒரு வாகனம் அதே தூரத்தை மறுபடியும் y (40 கி.மீ./மணி), வேகத்தில் கடக்கிறது என்றால் அந்த வாகனத்தின் சராசரி வேகம் x மற்றும் y -ன் இசைச் சராசரியாகும் (48 கி.மீ./மணி). மேலும் அவ்வாகனம் பயணம் செய்த மொத்த நேரமும் அவ்வாகனம் முழு தூரத்தையும் சராசரி வேகத்தில் பயணம் செய்திருந்தால் எடுத்துக் கொள்ளும் நேரமும் சமமாக இருக்கும்.

இதேபோல் ஒரு வாகனம் x (60கி.மீ./மணி) வேகத்தில் ஒரு குறிப்பிட நேரம் பயணம் செய்துவிட்டு மீண்டும் y (40கி.மீ./மணி) வேகத்தில் அதே அளவு நேரம் பயணம் செய்தால் அவ்வாகனத்தின் சராசரி வேகம் இரண்டு வேகங்களின் கூட்டுச் சராசரி (50 கி.மீ./மணி) ஆக இருக்கும்.

இம்முறையை இரண்டுக்கும் மேற்பட்ட உட்பயணங்களுக்கும் பயன்படுத்தலாம்:

வெவ்வேறு வேகங்களில் அமையும் ஒரு உட்பயணங்களின் தொடரில்: ஒவ்வொரு உட்பயணத்திலும் பயணம் செய்த தூரங்கள் சமமாக இருந்தால் மொத்தப் பயணத்தின் சராசரி வேகம், உட்பயணங்களின் வேகங்களின் இசைச் சராசரியாக அமையும்.

ஒவ்வொரு உட்பயணத்திலும் பயணம் செய்த காலங்கள் சமமாக இருந்தால் மொத்தப் பயணத்தின் சராசரி வேகம், உட்பயணங்களின் வேகங்களின் கூட்டுச் சராசரியாக அமையும்.

இரண்டுவிதமாகவும் இல்லையெனில் எடையிடப்பட்ட இசைச் சராசரி அல்லது எடையிடப்பட்ட கூட்டுச் சராசரி தேவைப்படும்.

• இரு மின் தடையங்கள் இணைமுறையில் இணக்கப்பட்டுள்ளது என்க:

ஒன்றின் மின்தடை x (60Ω) , மற்றொன்றின் மின்தடை y (40Ω) என்க. இவ்விணைப்பின் விளைவு x , y -ன் இசைச் சராசரி (48Ω). இது ஒவ்வொன்றும் சம அளவு மின் தடையுள்ள இரண்டு மின் தடயங்களை ஒருங்கே பயன்படுத்துவதற்குச் சமமாக அமையும். ஒவ்வொன்றின் மின் தடை 24Ω ஆகும்.

மாறாக இரு மின் தடயங்களும் தொடர்முறையில் இணைக்கப்பட்டால்:

சராசரி மின் தடை x மற்றும் y -ன் கூட்டுச் சராசரியாகும் (50Ω). (இணைப்பின் மொத்த மின் தடை x மற்றும் y -ன் கூடுதல்).

முந்தைய எடுத்துக்காட்டில் கூறியது போல இரண்டிற்கும் மேற்பட்ட மின் தடயங்களுக்கும் இம்முறையில் சராசரி மின் தடை காணலாம்.

பிற அறிவியல் துறைகளில்

வாயு ஆற்றலால் இயங்கும் ஒரு நீர் ஏற்றி, ஒரு குளத்திலுள்ள நீர் முழுவதையும் 4 மணி நேரத்தில் வெளியேற்றி விடும். மின் ஆற்றலால் இயங்கும் ஒரு நீர் ஏற்றி, அதே குளத்தை 6 மணி நேரத்தில் வெளியேற்றும். இரண்டு நீர் ஏற்றிகளும் ஒன்றாகச் சேர்ந்து அக்குளத்தின் நீர் முழுவதையும் (6 · 4)/(6 + 4), அதாவது 2.4 மணி நேரத்தில் வெளியேற்றும். இம்மதிப்பு 6, 4 இரண்டின் இசைச் சராசரியில் சரிபாதியாகும்.

நீரியலில், நீரோட்டம் மேற்பரப்பிற்கு செங்குத்தாக இருக்கும்போது நீரழுத்தக் கடத்தும் திறன் சராசரி காண இசைச் சராசரியும் நீரோட்டம் மேற்பரப்பிற்கு இணையாக இருக்கும்போது கூட்டுச் சராசரியும் பயன்படுத்தப்படுகிறது. முன்பு இயற்பியலில் பார்த்த எடுத்துக்காட்டுக்கும் இந்த எடுத்துக்காட்டுக்கும் சராசரி காண்பதில் உள்ள வேறுபாட்டிற்குக் காரணம் நீரியலில் பயன்படுத்தப்படும் கடத்தும் திறன் மின் தடைத் திறனுக்குத் தலைகீழியாக அமைவதுதான்.

தானியங்கிகளில் எரிபொருள்-சிக்கனத்திற்கு, மைல்/காலன்(mpg) அல்லது 100 கி.மீ. தூரத்துக்குத் தேவையான எரிபொருள் (லிட்டரில்) ஆகிய இருவகையான அளவுகள் கணக்கில் எடுத்துக் கொள்ளப்படுகின்றன. இவ்விரண்டு அளவுகளும் ஒன்றுக்கொன்று எதிர்விகிதத்தில் அமைகின்றன. (ஒன்று தூரம்/கனஅளவு, மற்றது கனஅளவு/தூரம்.) ஒரு வகைக் கார்களின் எரிபொருள்-சிக்கனத்தின் சராசரி மதிப்பு காணும்போது ஒரு அளவின் வாயிலாகக் காணப்படும் சராசரி மற்றொன்றின் வாயிலாகக் காணப்படும் இசைச்சராசரியாகும்.

பொருளியல்

விலை/வருவாய் போன்ற விகிதங்களின் சராசரி காணும்போது கூட்டுச் சராசரியைவிட இசைச் சராசரிக்குத்தான் முன்னுரிமை அளிக்கப்படுகிறது. ஏனெனில் இது போன்ற விகிதங்களின் சராசரி காண கூட்டுச் சராசரியைப் பயன்படுத்தினால் தரவின் உயர் உறுப்புகள் அதிக அளவிலும் கீழ்மட்ட உறுப்புகள் குறைந்த அளவிலும் எடையிடப்பட்டு விடக்கூடிய நிலை ஏற்படும். மாறாக இசைச் சராசரி பயன்படுத்தப்பட்டால் தரவின் அனைத்து உறுப்புகளும் சமமாக எடையிடப்படும்.^[3]

வடிவவியல்

• வடிவவியலில்ஒரு முக்கோணத்தின் உள்வட்ட ஆரம், அம்முக்கோணத்தின் குத்துக்கோடுகளின் நீளங்களின் இசைச் சராசரியில் மூன்றில் ஒரு பங்கு.
• ஒரு சமபக்க முக்கோணம் ABC -ன் சுற்றுவட்டத்தின் சிறுவில் BC -ன் மீது அமைந்த ஒரு புள்ளி P என்க. PB = q; PC = t என்க. PA, BC இரண்டும் வெட்டிக்கொள்ளும் புள்ளி P -லிருந்து உள்ள தூரம் y என்க.

y -ன் மதிப்பு q , t -ன் இசைச் சராசரியில் பாதி.^[4]

• ஒரு செங்கோண முக்கோணத்தில் செங்கோணத்தை உள்ளடக்கும் பக்கங்கள் a, b. மேலும் h -செம்பக்கத்திலிருந்து செங்கோணத்திற்கு வரையப்படும் குத்துயரம்.

h ², a² மற்றும் b² -ன் இசைச் சராசரியில் பாதி.^[5][6]

• கர்ணம் c கொண்ட செங்கோண முக்கோணத்துக்குள் வரையப்பட்ட இரு சதுரங்களின் பக்க நீளங்கள் t , s (t > s).

s² , c² மற்றும் t² -ன் இசைசராசரியில் பாதி..

• ஒரு சரிவகத்தின் உச்சிகள் முறையே A, B, C, D. சரிவகத்தின் இணைபக்கங்கள் AB, CD. மூலைவிட்டங்கள் வெட்டும் புள்ளி E. கோடு FEG , AB மற்றும் CD க்கு இணையாக இருக்குமாறு F, பக்கம் DA மீதும் G , பக்கம் BC மீதும் அமையும் புள்ளிகள்.

FG , AB மற்றும் DC -ன் இசைச் சராசரியாகும்.

குறுக்காக வைக்கப்பட்ட ஏணிகள். h -A மற்றும் B -ன் இசைச் சராசரி.

• இரு ஏணிகள் ஒரு பாதையின் இருபுறங்களிலும் உள்ள சுவர்கள் மீது அடிமுனை ஒரு சுவரின் அடித் தரையிலும் மறுமுனை எதிர்ச் சுவரிலும் இருக்குமாறு குறுக்காக சாத்தி வைக்கப்பட்டுள்ளன. சுவற்றின் அடியிலிருந்து ஏணிகளின் மேல் முனையின் உயரங்கள் முறை A , B. இரு ஏணிகளும் சந்திக்கும் இடத்தின் உயரம் தரையிலிருந்து h.

h , A மற்றும் B -ன் இசைச் சராசரியில் பாதி.

சுவர்கள் சாய்வாக ஆனால் இணையாக இருக்கும்போதும் மேலே கூறப்பட்ட முடிவு உண்மையாகும். ( உயரங்கள் A, B, h தரையிலிருந்து சுவற்றுக்கு இணையான கோட்டுத்திசைகளில் அளக்கப்பட வேண்டும்.)

• ஒரு நீள்வட்டத்தின் அரைச் செவ்வகலம், (சிற்றச்சுக்கு இணையாக குவியத்தின் வழி நீள்வட்டத்திற்கு வரையப்பட்ட கோட்டுத்துண்டின் நீளம்.) குவியத்திலிருந்து நீள்வட்டத்தின் பெரும மற்றும் சிறும தூரங்களின் இசைச் சராசரியாகும்.

முக்கோணவியலில்

முக்கோணவியலில்

${\displaystyle \tan A={\frac {a}{b}}}$

இதில் ${\displaystyle a,}$ ${\displaystyle b}$ மெய்யெண்கள்.

இருமடங்கு கோண வாய்ப்பாட்டை இசைச் சராசரி மூலம் மாற்றி எழுதலாம்:

${\displaystyle \tan 2A={\frac {2ab}{a+b}}*{\frac {1}{b-a}}}$

இவ்வாய்ப்பாட்டின் வலதுபுறமுள்ள ${\displaystyle {\frac {2ab}{a+b}},}$ a, b -ன் இசைச் சராசரி.

எடுத்துக்காட்டு:

${\displaystyle \tan A={\frac {3}{7}},}$

${\displaystyle \tan 2A={\frac {2*{\frac {3}{7}}}{1-({\frac {3}{7}})^{2}}}={\frac {21}{20}};}$

${\displaystyle \tan 2A={\frac {2*3*7}{3+7}}*{\frac {1}{7-3}}={\frac {21}{20}}.}$

இரு எண்களின் இசைச் சராசரி

${\displaystyle x_{1}}$ மற்றும் ${\displaystyle x_{2}}$, என்ற இரு எண்களின் இசைச் சராசரி:

${\displaystyle H={\frac {2x_{1}x_{2}}{x_{1}+x_{2}}}.}$

கூட்டுச் சராசரி: ${\displaystyle A={\frac {x_{1}+x_{2}}{2}}}$

பெருக்கல் சராசரி: ${\displaystyle G={\sqrt {x_{1}x_{2}}},}$

இவ்விரு எண்களின் இசைச் சராசரிக்கு கூட்டுச் சராசரி மற்றும் பெருக்கல் சராசரிகளுடனான தொடர்பு:

${\displaystyle H={\frac {G^{2}}{A}}.}$

ஃ ${\displaystyle G={\sqrt {AH}}}$,

இரு எண்களின் பெருக்கல் சராசரி அவ்வெண்களின் கூட்டு மற்றும் இசைச் சராசரிகளின் பெருக்கல் சராசரி என்பதைக் காட்டுகிறது. இத்தொடர்பை n உறுப்புகளுக்கு நீட்டிக்கலாம்.

இசைச் சராசரியின் பொது வாய்ப்பாட்டின்படி:

${\displaystyle H(x_{1},\ldots ,x_{n})={\frac {(G(x_{1},\ldots ,x_{n}))^{n}}{A(x_{2}x_{3}\cdots x_{n},x_{1}x_{3}\cdots x_{n},\ldots ,x_{1}x_{2}\cdots x_{n-1})}}={\frac {(G(x_{1},\ldots ,x_{n}))^{n}}{A\left({\frac {\prod _{i=1}^{n}x_{i}}{x_{1}}},{\frac {\prod _{i=1}^{n}x_{i}}{x_{2}}},\ldots ,{\frac {\prod _{i=1}^{n}x_{i}}{x_{n}}}\right)}}.}$

இதில் ${\displaystyle n=2}$ எனில்:

${\displaystyle H(x_{1},x_{2})={\frac {(G(x_{1},x_{2}))^{2}}{A(x_{2},x_{1})}}={\frac {(G(x_{1},x_{2}))^{2}}{A(x_{1},x_{2})}}}$

சராசரிச் செயலிகளைக் கொண்டு எழுத:

${\displaystyle H={\frac {G^{2}}{A}}}$