சரிவகம்

இயூக்கிளிடிய வடிவியலில், ஒரு சரிவகம் (trapezoid^[1] அல்லது trapezium) என்பது ஒரு சோடி எதிர்ப்பக்கங்கள் ஒன்றுக்கொன்று சமாந்தரமாக (இணையாக) அமைந்துள்ள ஒரு குவிவு நாற்கரம் ஆகும். இரு சோடி எதிர்ப்பக்கங்களும் இணையாக உள்ள சரிவகம் இணைகரம் என்று அழைக்கப்படும்.^[2]

சரிவகம் Trapezoid Trapezium
சரிவகம்
வகை	நாற்கரம்
விளிம்புகள் மற்றும் உச்சிகள்	4
பரப்பளவு	${\displaystyle {\tfrac {a+b}{2}}h}$
பண்புகள்	குவிவுப் பல்கோணம்

இணை பக்கங்கள் இரண்டும் சரிவகத்தின் "அடிப்பக்கங்கள்" எனவும், மற்ற இணையற்ற இரு பக்கங்களும் "தாங்கி பக்கங்கள்" எனவும் அழைக்கப்படும். இரு சோடி எதிர்ப்பக்கங்களும் இணையானவையாக இருந்தால், சரிவகம் ஒரு இணைகரமாகி விடும். இந்நிலையில் அதற்கு இரு சோடி இணை பக்கங்களும் அடிப்பக்கங்களாக இருக்கும். எந்த பக்கங்களும் சமமாக இல்லாவிடில் அச்சரிவகம், "அல்சமபக்கச் சரிவகம்" எனப்படும்.^[3]

மாறுபட்ட வரையறைகள்

இரு சோடி இணைபக்கங்களுடைய இணைகரங்களைச் சரிவகங்களாக எடுத்துக்கொள்ளலாமா இல்லையா என்பதில் கருத்து வேறுபாடு உள்ளது. சிலர் சரிவகத்தை ஒரேயொரு சோடி இணைபக்கங்கள் கொண்ட நாற்கரமாகவும், வேறு சிலர் குறைந்தது ஒரு சோடி இணைபக்கங்கள் கொண்ட நாற்கரமாகவும் வரையறுக்கின்றனர். முதல் வரையறையின் படி இணைகரங்களை சரிவகங்களாகக் கருத முடியாது.^[4] Others^[1] இரண்டாவது வரையறையின்படி இணைகரங்கள் ஒரு சிறப்புவகையான சரிவகங்களாக இருக்கும்.^[5])

நுண்கணிதம் போன்ற உயர் கணிதத்தில் இரண்டாவது வரையறை பயனுள்ளதாக அமைகிறது. இந்தக் கட்டுரையிலும் இரண்டாவது வரையறையே கணக்கில் கொள்ளப்படுகிறது. சாய்சதுரங்கள், செவ்வகங்கள், சதுரங்கள் உட்பட்ட அனைத்து இணைகரங்களும் சரிவகங்களாகும். செவ்வகங்கள் நடு-விளிம்புகளைப் பொறுத்து ஆடி சமச்சீர்மை உடையது; சாய்சதுரங்கள் உச்சிகளில் ஆடி சமச்சீர்மை கொண்டவை; சதுரங்கள் நடு-விளிம்புகள், உச்சிகள் இரண்டையும் பொறுத்து ஆடி சமச்சீர்மை உடையவை.

சிறப்பு வகைகள்

சரிவக வகைகள். ஆரஞ்சுநிற வடிவங்கள் இணைகரங்களாகவும் கொள்ளப்படும்.

• இரு அடுத்துள்ள கோணங்களைச் செங்கோணங்களாகக் கொண்ட சரிவகம், நேர் சரிவகம்

• நீள அடிப்பக்கத்தின் இரு அடுத்துள்ள கோணங்களைக் குறுங்கோணங்களாகக் கொண்ட சரிவகம், குறு சரிவகம் (acute trapezoid) என்றும் ஒவ்வொரு அடிப்பக்கத்தின் இரு அடுத்துள்ள கோணங்களில் ஒன்று குறுங்கோணமாகவும் மற்றொன்று விரிகோணமாகவும் இருந்தால் அச்சரிவகம் விரி சரிவகம் (obtuse trapezoid) எனவும் அழைக்கப்படுகிறது.

• அடிப்பக்க கோணங்கள் இரண்டும் சமமாக இருந்தால் அச்சரிவகம், இருசமபக்க சரிவகம் ஆகும். இருசமபக்க சரிவகத்தின் இரு தாங்கிப் பக்கங்களும் சமமாக இருப்பதோடு எதிரொளிப்பு சமச்சீர்மை கொண்டவையாக இருக்கும். இது குறு சரிவகங்களுக்கும் நேர் சரிவகங்களுக்கும் சாத்தியமாகும்.

• இரு சோடி எதிர்ப்பக்கங்களும் இணையாகவுள்ள சரிவகம் இணைகரம் ஆகும்.

• தொடு சரிவகம் என்பது அதன் நான்கு பக்கங்களும் அதனுள் அமையும் வட்டத்துக்குத் தொடுகோடுகளாக அமைந்துள்ள சரிவகம்.

சரிவகம் அமைவதற்கான நிபந்தனைகள்

a, c, b, d - நான்கு பக்கங்களின் நீளங்கள் எனில்,

• a, b பக்கங்களை மட்டும் இணையாகக் கொண்ட சரிவகம் அமையக் கட்டுபாடு:^[6]

${\displaystyle \displaystyle |d-c|<|b-a|<d+c.}$

• இணைகரமாக இருப்பதற்கான கட்டுபாடு:

${\displaystyle d-c=b-a=0}$

${\displaystyle |d-c|=|b-a|\neq 0}$ ஆக இருந்தால் வெளி-தொடு நாற்கரமாக இருக்கும் (வெளி-தொடு நாற்கரம் ஒரு சரிவகம் இல்லை).^{[7]:p. 35}

பண்பாக்கங்கள்

சரிவகம்:
இணை பக்கங்கள்: ${\displaystyle a,\,b}$ (${\displaystyle a<b)}$
தாங்கிகள்: ${\displaystyle c,\,d}$
மூலைவிட்டங்கள்: ${\displaystyle q,\,p}$
நடுக்கோட்டு நீளம்: ${\displaystyle m}$
உயரம்: ${\displaystyle h}$

சரிவகத்தின் மூலைவிட்டங்களால் உண்டான எதிர் முக்கோணங்கள் ${\displaystyle S,\,T}$

ஒரு குவிவு நாற்கரத்தில், கீழே தரப்பட்டுள்ள பண்புகள் அனைத்தும் சமானமானவை என்பதுடன் அவை ஒவ்வொன்றும் அந்நாற்கரம் சரிவகமாக இருப்பதற்கான என்பதைக் காட்டுகிறது:

• இரு அடுத்துள்ள கோணங்கள் மிகைநிரப்பு கோணங்கள் (அதாவது கூட்டுத்தொகை 180 பாகைகள்.
• ஒரு பக்கம் மற்றும் ஒரு மூலைவிட்டத்திற்கு இடைப்பட்ட கோணம், எதிர்ப்பக்கத்திற்கும் அதே மூலைவிட்டத்திற்கும் இடைப்பட்ட கோணத்திற்குச் சமம்.
• மூலைவிட்டங்கள் ஒன்றையொன்று ஒரே விகிதத்தில் வெட்டிக்கொள்கின்றன (இந்த விகிதம், இணை பக்கங்களின் விகிதத்திற்குச் சமம்)
• மூலைவிட்டங்கள் நாற்கரத்தை நான்கு முக்கோணங்களாகப் பிரிக்கும். அவற்றுள் ஒரு சோடி எதிர் முக்கோணங்கள் சம பரப்பளவு கொண்டவை.^[7]:Prop.5
• ஒரு மூலைவிட்டத்தால் கிடைக்கும் இரு முக்கோணங்களின் பரப்பளவுகளின் பெருக்குத்தொகை, மற்றொரு மூலைவிட்டத்தால் கிடைக்கும் இரு முக்கோணங்களின் பரப்பளவுகளின் பெருக்குத்தொகைக்குச் சமமாக இருக்கும்.^[7]:Thm.6
• மூலைவிட்டங்களால் உருவாகும் நான்கு முக்கோணங்களில் ஏதாவது இரு முக்கோணங்களின் பரப்பளவுகள் S, T எனில், கீழுள்ள சமன்பாடு நிறைவு செய்யப்படும்.

${\displaystyle {\sqrt {K}}={\sqrt {S}}+{\sqrt {T}},}$ (K - நாற்கரத்தின் பரப்பளவு)^[7]:Thm.8

• இரு எதிர்ப்பக்கங்களின் நடுப்புள்ளிகளும் மூலைவிட்டங்கள் வெட்டிக்கொள்ளும் புள்ளியும் ஒரே கோட்டிலமையும்.^[7]:Thm.15
• ABCD நாற்கரத்தின் கோணங்கள் பின்வரும் முடிவை நிறைவு செய்யும்:

${\displaystyle \sin A\sin C=\sin B\sin D.}$^{[7]:p. 25}

• இரு அடுத்துள்ள கோணங்களின் கோசைன் மதிப்புகளின் கூடுதல் பூச்சியமாக இருக்கும். இது மற்ற இரு அடுத்துள்ள கோணங்களுக்கும் பொருந்தும்.^{[7]:p. 25}
• இரு அடுத்துள்ள கோணங்களின் கோடேன்ஜென்ட்டின் மதிப்புகளின் கூடுதல் பூச்சியமாக இருக்கும். இது மற்ற இரு அடுத்துள்ள கோணங்களுக்கும் பொருந்தும்.^{[7]:p. 26}
• நாற்கரத்தின் இருநடுக்கோடுகளில் (எதிர்ப்பக்கங்களின் நடுப்புள்ளிகளை இணைக்கும் கோட்டுத்துண்டு) ஒன்று, நாற்கரத்தை சம பரப்பளவுள்ள இரு நாற்கரங்களாகப் பிரிக்கும்.^{[7]:p. 26}
• இரு எதிர்ப்பக்கங்களின் நடுப்புள்ளிகளை இணைக்கும் இருநடுக்கோட்டின் நீளத்தின் இருமடங்கு, நாற்கரத்தின் மற்ற இரு பக்க நீளங்களின் கூட்டுத்தொகைக்குச் சமம்.^{[7]:p. 31}

கூடுதலாகப் பின்னுள்ள பண்புகள் சமானமானவை; எதிர்ப்பக்கங்கள் a, b இணை என்பதைத் தருகிறது.

• தொடர்ச்சியான நான்கு பக்கங்கள் a, c, b, d மற்றும் மூலைவிட்டங்கள் p, q நிறைவுசெய்யும் சமன்பாடு:^[7]:Cor.11

${\displaystyle p^{2}+q^{2}=c^{2}+d^{2}+2ab.}$

• மூலைவிட்டங்களின் நடுப்புள்ளிகளுக்கு இடைப்பட்ட தூரம் v நிறைவு செய்யும் சமன்பாடு:^[7]:Thm.12

${\displaystyle v={\frac {|a-b|}{2}}.}$

நடுக்கோடும் உயரமும்

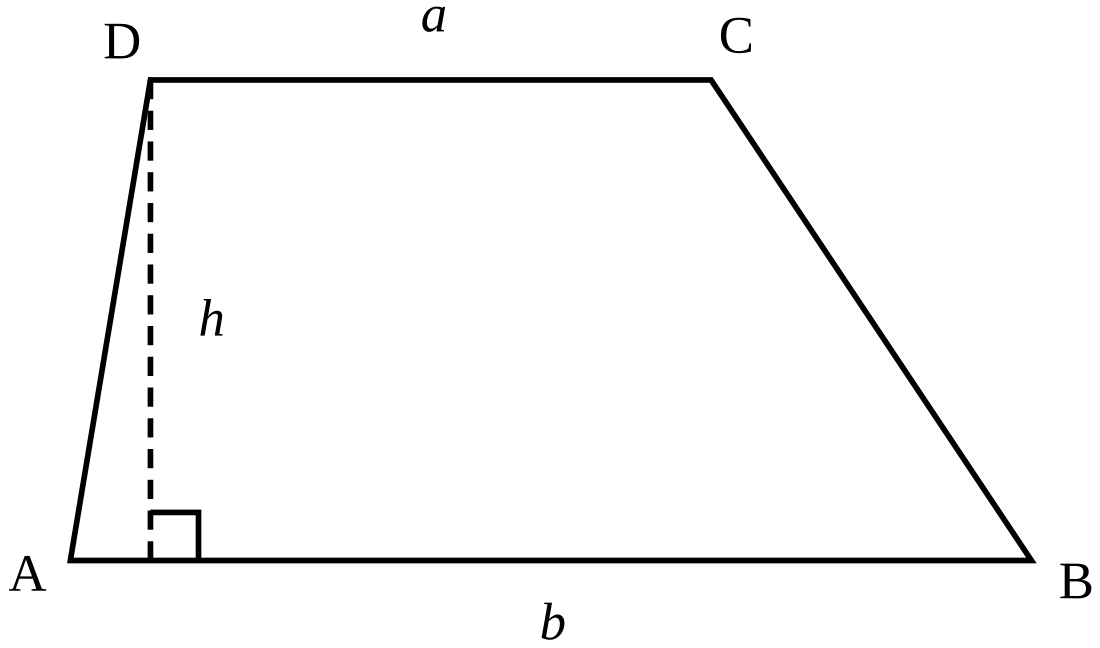
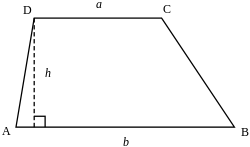
சரிவகத்தின் தாங்கிப் பக்கங்களின் நடுப்புள்ளிகளை இணைக்கும் கோட்டுத்துண்டு சரிவகத்தின் "நடுக்கோடு" ஆகும். இந்த நடுக்கோடு இரு இணை அடிப்பக்கங்களுக்கும் இணையாக இருக்கும். இதன் நீளம் (m) அடிப்பங்களின் நீளங்களின் (a, b) சரிசரியாக இருக்கும்.^[1]

${\displaystyle m={\frac {a+b}{2}}.}$

சரிவகத்தின் "உயரம்" என்பது அதன் இணை அடிப்பக்கங்களுக்கு இடைப்பட்ட செங்குத்து தூரமாகும். அடிப்பக்கங்களின் நீளங்கள் சமமில்லையென்றால் (a ≠ b) சரிவகத்தின் உயரத்தை அதன் நான்கு பக்கங்களின் நீளங்களைக் கொண்டு காணும் வாய்பாடு:^[1]

${\displaystyle h={\frac {\sqrt {(-a+b+c+d)(a-b+c+d)(a-b+c-d)(a-b-c+d)}}{2|b-a|}}}$ ( a, b இணை பக்கங்கள்; c, d தாங்கி பக்கங்கள்)

பரப்பளவு

சரிவகத்தின் பரப்பளவு K:^[1]

${\displaystyle K={\frac {a+b}{2}}\cdot h=mh}$

a, b - இணை பக்கங்களின் நீளங்கள்; h - உயரம்; m - இணை பக்க நீளங்களின் கூட்டுச் சராசரி. கிபி 499 இல், பண்டைய இந்தியக் கணிதவியலாளரும் வானிலையாளருமான ஆரியபட்டர் அவரது ஆர்யபட்டியம் (பிரிவு 2.8) நூலில் இதனைப் பயன்படுத்தியுள்ளார். ஒரு சரிவகத்தின் ஒரு இணைபக்கம் புல்ளியாகச் சுருங்குவதால் கிடைப்பதாக ஒரு முக்கோணத்தைக் கொண்டால் இவ்வாய்பாட்டின் சிறப்பு வகையாக, முக்கோணத்தின் பரப்பளவுக்கான வாய்பாட்டைப் பெறலாம்.

7 ஆம் நூற்றாண்டின் இந்தியக் கணிதவியலாளர் முதலாம் பாஸ்கரர் கீழ்வரும் வாய்பாட்டைத் தருவித்தார்: சரிவகத்தின் தொடர்ச்சியான நான்கு பக்கங்களின் நீளங்கள் a, c, b, d எனில் சரிவகத்தின் பரப்பளவு:

${\displaystyle K={\frac {1}{2}}(a+b){\sqrt {c^{2}-{\frac {1}{4}}\left((b-a)+{\frac {c^{2}-d^{2}}{b-a}}\right)^{2}}}}$ a, b இணை பக்கங்கள்; b > a.^[8]

இவ்வாய்பாட்டை மேலும் சமச்சீரான வடிவில் காரணிப்படுத்தி எழுதலாம்:^[1]

${\displaystyle K={\frac {a+b}{4|b-a|}}{\sqrt {(-a+b+c+d)(a-b+c+d)(a-b+c-d)(a-b-c+d)}}.}$

இணை பக்கங்களில் ஒன்று புள்ளியாகச் சுருங்கினால் ( a = 0), இந்த வாய்பாடு முக்கோணத்தின் பரப்பளவிற்கான ஈரோனின் வாய்பாடாகக் கிடைக்கும்.

ஈரோனின் வாய்பாட்டை ஒத்த, சரிவகப் பரப்பளவுக்கான மற்றொரு வாய்பாடு:^[1]

${\displaystyle K={\frac {a+b}{|b-a|}}{\sqrt {(s-b)(s-a)(s-b-c)(s-b-d)}},}$ ${\displaystyle s={\tfrac {1}{2}}(a+b+c+d)}$ - சரிவகத்தின் அரைச்சுற்றளவு.

பொது நாற்கரத்துக்கான பிரெட்ஷ்ணைடரின் வாய்பாட்டின் சிறப்பு வகையாகவும் இவ்வாய்பாடு உள்ளது.

பிரெட்ஷ்ணைடரின் வாய்பாட்டிலிருந்து கிடைப்பது:

${\displaystyle K={\sqrt {{\frac {(ab^{2}-a^{2}b-ad^{2}+bc^{2})(ab^{2}-a^{2}b-ac^{2}+bd^{2})}{4(b-a)^{2}}}-\left({\frac {c^{2}+d^{2}-a^{2}-b^{2}}{4}}\right)^{2}}}.}$

இணை பக்கங்களின் நடுப்புள்ளிகளை இணைக்கும் கோடு சரிவகத்தின் பரப்பளவை இருசமக்கூறிடும்.

மூலைவிட்டங்கள்

சரிவகத்தின் மூலைவிட்டங்களின் நீளங்கள்^[1]

${\displaystyle p={\sqrt {\frac {ab^{2}-a^{2}b-ac^{2}+bd^{2}}{b-a}}},}$

${\displaystyle q={\sqrt {\frac {ab^{2}-a^{2}b-ad^{2}+bc^{2}}{b-a}}}}$

a - சிறிய அடிப்பக்கம்; b - பெரிய அடிப்பக்கம்; c, d தாங்கி பக்கங்கள்.

AC, BD மூலைவிட்டங்கள் வெட்டிக்கொள்ளும் புள்ளி O. இம்மூலைவிட்டங்களால் சரிவகம் நான்கு முக்கோணங்களாகப் பிரிக்கப்படுகிறது (படம்).

• ${\displaystyle \triangle AOD}$ இன் பரப்பளவு = ${\displaystyle \triangle BOC}$ இன் பரப்பளவு}
• ${\displaystyle \triangle AOD}$, ${\displaystyle \triangle BOC}$ முக்கோணங்களின் பரப்பளவுகளின் பெருக்குத்தொகையும் ${\displaystyle \triangle AOB}$, ${\displaystyle \triangle COD}$ முக்கோணங்களின் பெருக்குத்தொகையும் சமம்.
• அடுத்துள்ள முக்கோணங்களின் பரப்பளவுகளின் விகிதம், இணை அடிப்பக்க நீளங்களின் விகிதத்திற்குச் சமம்.^[1]

சரிவகத்தின் வரிசையான உச்சிகள் A, B, C, D; இணை பக்கங்கள் AB, DC; மூலைவிட்டங்கள் வெட்டும் புள்ளி E; F, DA பக்கத்தின் மீதும், G, BC பக்கத்தின் மீதும் FEG ஆனது AB, CD க்கு இணையாக உள்ளவாறு அமையும் புள்ளிகள் எனில், AB, DC இன் இசைச் சராசரி FG ஆகும்:^[9]

${\displaystyle {\frac {1}{FG}}={\frac {1}{2}}\left({\frac {1}{AB}}+{\frac {1}{DC}}\right).}$

இணையில்லாத இரு பக்கங்களின் நீட்டிப்புக்கோடுகள் வெட்டும் புள்ளி மற்றும் மூலைவிட்டங்கள் வெட்டும் புள்ளி வழியாகச் செல்லும் கோடானது, அடிப்பக்கம் ஒவ்வொன்றையும் இருசமக்கூறிடும்^[10]

பிற பண்புகள்

சரிவகத்தின் பரப்பளவின் மையம், இணை பக்கங்களின் நடுப்புள்ளிகளை இணைக்கும் கோட்டின் மீதமையும். இந்த மையம், நீளமான இணைபக்கம் b இலிருந்து உள்ள செங்குத்து தூரம் x:^[11]

${\displaystyle x={\frac {h}{3}}\left({\frac {2a+b}{a+b}}\right).}$

இக்கோட்டுத்துண்டை பரப்பளவு மையம் பிரிக்கும் விகிதம் (சிறிய இணை பக்கத்திலிருந்து நீள இணை பக்கத்துக்கு எடுத்துக்கொள்ள)^{[12]:p. 862}

${\displaystyle {\frac {a+2b}{2a+b}}.}$

A, B கோணங்களின் இரு சமவெட்டிகள் வெட்டும் புள்ளி P; C, D கோணங்களின் இருசமவெட்டிகள் வெட்டும் புள்ளி Q எனில்:^[10]

${\displaystyle PQ={\frac {|AD+BC-AB-CD|}{2}}.}$