முகம் (வடிவவியல்)

திண்ம வடிவவியலில் முகம் (face) என்பது ஒரு திண்மப்பொருளின் வரம்பின் ஒரு பகுதியாக அமைந்திருக்கும் தட்டையான மேற்பரப்பு ஆகும்.^[1] இத்தகைய முகங்களால் மட்டுமே அடைபெறும் முப்பரிமாணத் திண்மம், பன்முகியாகும்.

உயர்பரிமாண பல்பரப்புகளில் "முகம்" என்ற சொல்லானது அந்தப் பல்பரப்பின் வெவ்வேறு பரிமாணக் கூறுகளைக் (0-முகம், 1-முகம், 2-முகம், 3-முகம்.....) குறிக்கப் பயன்படுத்தப்படுகிறது.^[2]

பல்கோண முகம்

கனசதுரத்தின் முகங்களாகச் சதுரங்கள்.

நாற்பரிமாணக் கனசதுரம் அல்லது மீச்சதுரம்

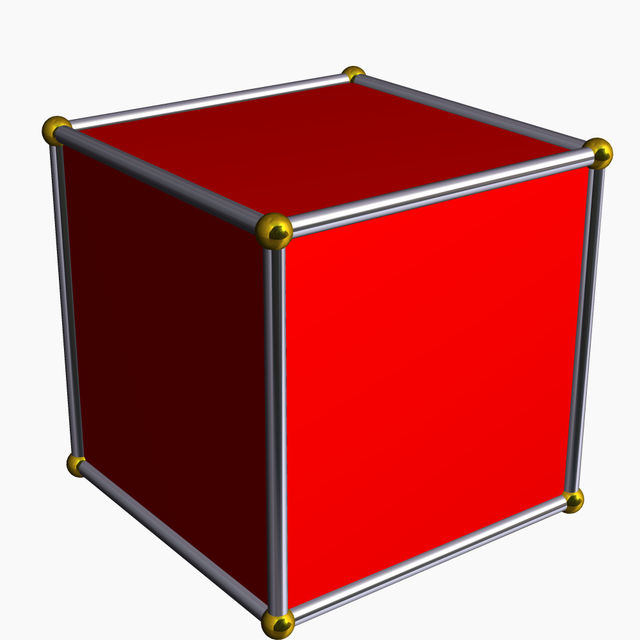
அடிப்படை வடிவவியலில் ஒரு பன்முகியின் வரம்பில் அமைந்துள்ள ஒரு பல்கோணம் அப்பன்முகியின் "முகம்" என அழைக்கப்படுகிறது.^{[note 1][2][3]} பன்முகியின் பல்கோண முகமானது அந்தப் "பன்முகியின் பக்கம்" எனவும் அழைக்கப்படுகிறது.

படத்தில் ஒரு கனசதுரத்தின் (பன்முகி) முகங்களாக ஆறு சதுரங்கள் (பல்கோணம்) இருப்பதைக் காணலாம்.

சிலசமயங்களில் ஒரு 4-பல்பரப்பின் இருபரிமான இயல்புகளைக் குறிக்கவும் இச்சொல் பயன்படுத்தப்படுகிறது. இதன்படி ஒரு நாற்பரிமாணக் கனசதுரம் 24 முகங்கள் கொண்டது; அவை ஒவ்வொன்றும் அந்த நாற்பரிமாணக் கனசதுரத்தின் 8 கனசதுரச் சிற்றறைகளில் இரண்டைப் பகிர்ந்து கொண்டிருக்கும் (படத்தில் காணவும்).

பன்முகியின் பல்கோணப் பக்கங்களின் எண்ணிக்கை

ஒரு குவிவுப் பன்முகியின் பக்கங்களின் எண்ணிக்கை கீழுள்ள "ஆய்லர் பண்பை" நிறைவு செய்யும்:

${\displaystyle V-E+F=2,}$

இதில்,

• V - பன்முகியின் உச்சிகளின் எண்ணிக்கை
• E - பன்முகியின் விளிம்புகளின் எண்ணிக்கை
• F - பன்முகியின் முகங்களின் எண்ணிக்கை

இச்சமன்பாடு "ஆய்லரின் பன்முகி வாய்பாடு" என அழைக்கப்படுகிறது^[4][5].

இச்சமன்பாட்டிலிருந்து ஒரு பன்முகியின் முகங்களின் எண்ணிக்கையானது, அதன் விளிம்புகளின் எண்ணிக்கையிலிருந்து உச்சிகளின் எண்ணிக்கையைக் கழித்துக் கிடைக்கும் எண்ணைவிட இரண்டு அதிகமாக இருக்கும் என அறியலாம்.

கனசதுரத்தின் உச்சி, விளிம்பு, முகம்

எடுத்துக்காட்டு: ஒரு கனசதுரத்தில்

V - உச்சிகளின் எண்ணிக்கை = 8

E - விளிம்புகளின் எண்ணிக்கை = 12.

F - முகங்களின் எண்ணிக்கை = (12 - 8) + 2 = 6

k-முகம்

உயர்பரிமாண வடிவவியலில், ஒரு பல்பரப்பின் முகங்கள் என்பது அந்தப் பல்பரப்பின் எல்லாப் பரிமாணக் கூறுகளையும் குறிக்கும்.^[2][6][7] k பரிமாணத்திலமைந்த முகமானது k-முகம் எனப்படும். எடுத்துக்காட்டாக, முப்பரிமாணப் பன்முகிகளின் பல்கோண முகங்கள் இருபரிமாண வடிவங்கள். எனவே அவை பன்முகியின் 2-முகங்கள் எனப்படுகின்றன.

கணக் கோட்பாட்டில் ஒரு பல்பரப்பின் முகங்கள் அடங்கிய கணத்தில் அப்பல்பரப்பு ஒரு முகமாகவும், வெற்றுக் கணம் -1 பரிமாண முகமாகவும் சேர்க்கப்படுகின்றன. எந்தவொரு n-பல்பரப்புக்கும் (n-பரிமாணப் பல்பரப்பு) k இன் மதிப்பானது −1 ≤ k ≤ n என்றபடி இருக்கும்.

இவ்விளக்கத்தை கனசதுரம் மற்றும் 4-பல்பரப்பு ஆகியவற்றின் மூலம் புரிந்து கொள்ளலாம்.

• கனசதுரத்தில் முகங்களின் கணத்திலுள்ள உறுப்புகள்:
  • அக்கனசதுரம் (3-முகம்; கனசதுரத்தின் முப்பரிமாணக் கூறு)
  • கனசதுரத்தை அடைக்கும் 6 சதுரங்கள் (2-முகங்கள், கனசதுரத்தின் இருபரிமாணக் கூறுகள்)
  • கனசதுரத்தின் விளிம்புகள் (1-முகங்கள், கனசதுரத்தின் ஒருபரிமாணக் கூறுகள்),
  • கனசதுரத்தின் உச்சிகள் (0-முகங்கள், கனசதுரத்தின் 0-பரிமாணக் கூறுகள்)
  • வெற்றுக் கணம். (இதன் பரிமாணம் −1 என எடுத்துக்கொள்ளப் படுகிறது)

• 4-பல்பரப்பின் (நான்கு பரிமாண பல்பரப்பு) முகங்களின் கணத்திலுள்ள உறுப்புகள்:
  • அந்த 4-பல்பரப்பு (4-முகம்)
  • பல்பரப்பின் 3-பரிமாண பன்முகிச் சிற்றறைகள் (cells)
  • பல்பரப்பின் 2-பரிமாண பல்கோண வடிவ மேடுகள் (Ridges)
  • பல்பரப்பின் 1-பரிமாண விளிம்புகள் (கோட்டுத்துண்டுகள்)
  • பல்பரப்பின் 0-பரிமாண உச்சிகள் (புள்ளிகள்
  • வெற்றுக் கணம். (இதன் பரிமாணம் −1 என எடுத்துக்கொள்ளப் படுகிறது.)

மீமுகம் அல்லது (n − 1)-முகம்

உயர்பரிமாண வடிவவியலில் ஒரு n-பல்பரப்பின் (n-1)-முகங்கள் (பல்பரப்பின் பரிமாணத்தைவிட ஒரு பரிமாணம் குறைவான முகங்கள் அப்பல்பரப்பின் "முகப்புகள்" (facets) அல்லது (மீமுகங்கள்" (hyperfaces) என அழைக்கப்படுகின்றன.^[8][9] பல்பரப்பு அதன் மீமுகங்களால் அடைக்கப் படுகிறது.

எடுத்துக்காட்டு:

• ஒரு கோட்டுத்துண்டின் மீமுகங்கள் அதன் தொடக்க மற்றும் முடிவுப் புள்ளிகள் (0-முகங்கள்).
• ஒரு பல்கோணத்தின் மீமுகங்கள் அதன் விளிம்புகள் (1-முகங்கள்).
• ஒரு பன்முகியின் மீமுகங்கள் அதன் பல்கோண முகங்கள் (2-முகங்கள்).
• ஒரு 4-பல்பரப்பின் மீமுகங்கள் அதன் முப்பரிமானக் கூறுகளான சிற்றறைகள் (3-முகங்கள்)
• ஒரு 5-பல்பரப்பின் மீமுகங்கள் அதன் 4-முகங்கள்

மேடு அல்லது (n − 2)-முகம்

ஒரு n-பல்பரப்பின் (n-2)-முகங்கள் (பல்பரப்பின் பரிமாணத்தைவிட இரண்டு பரிமாணம் குறைவான முகங்கள்) அப்பல்பரப்பின் "முகடுகள்" அல்லது மேடுகள்" (ridges) அல்லது உள்முகப்புகள் (subfacets) என அழைக்கப்படுகின்றன.^[10] ஒரு பல்பரப்பின் இரண்டே இரண்டு மீமுகங்களின் வரம்பாக மேடுகள் அமைகின்றன.

எடுத்துக்காட்டு:

• இரு பரிமாணப் பல்கோணத்தின் மேடுகள் அதன் உச்சிகள் (0-முகங்கள்).
• முப்பரிமாணப் பன்முகியின் மேடுகள் அதன் விளிம்புகள் (1-முகங்கள்).
• 4-பல்பரப்பின் மேடுகள் அவற்றின் இருபரிமாண முகங்கள் (2-முகங்கள்)
• 5-பல்பரப்பின் மேடுகள் அதன் முப்பரிமாணச் சிற்றறைகள் (3-முகங்கள்).

சிகரம் அல்லது (n − 3)-முகங்கள்

ஒரு n-பல்பரப்பின் (n − 3)-முகங்கள் அதன் உச்சங்கள் அல்லது சிகரங்கள் (peaks) என அழைக்கப்படுகின்றன. ஒரு ஒழுங்கு பல்பரப்பின் சிகரமானது, அதன் முகப்புகளின் சுழற்சி அச்சுகளையும் மேடுகளையும் கொண்டிருக்கும்.

எடுத்துக்காட்டு:

• முப்பரிமாணப் பன்முகிக்கு அதன் உச்சிகள் (0-முகங்கள்) சிகரங்கள் ஆகும்.
• 4-பல்பரப்பின் சிகரங்கள் அதன் விளிம்புகளாகும் (1-முகங்கள்).
• 5-பரிமாணப் பல்பரப்பின் சிகரங்கள் அதன் முகங்களாகும் (2-முகங்கள்).

குறிப்புகள்

1. Some other polygons, which are not faces, are also important for polyhedra and tilings. These include Petrie polygons, vertex figures and facets (flat polygons formed by coplanar vertices that do not lie in the same face of the polyhedron).