Гіпотеза Рімана

Гіпотеза Рімана — математична гіпотеза про те, що дзета-функція Рімана ${\displaystyle \displaystyle \zeta (s)}$ (введена Ейлером 1737 року) набуває нульових значень тільки у від'ємних парних числах: ${\displaystyle 0=\zeta (-2)=\zeta (-4)=\zeta (-6)=\dots }$ (де ці прості нулі називають «тривіальними» нулями дзета-функції), і комплексних числах із дійсною частиною ${\displaystyle {1 \over 2}}$ («нетривіальні» нулі дзета-функції Рімана). Гіпотеза Рімана стосується розташування цих нетривіальних нулів і стверджує, що:

Всі нетривіальні нулі дзета-функції мають дійсну частину, рівну ${\displaystyle {1 \over 2}}$.

Проблеми тисячоліття
Рівність класів P і NP
Гіпотеза Годжа
Гіпотеза Пуанкаре*
Гіпотеза Рімана
Квантова теорія Янга — Мілса
Рівняння Нав'є — Стокса
Гіпотеза Берча і Свіннертона-Даєра
* доведені

Отже, якщо гіпотеза істинна, всі нетривіальні нулі дзета-функції Рімана (число яких нескінченне) лежать на критичній прямій ${\displaystyle \operatorname {Re} \,s={\frac {1}{2}}}$, що складається з комплексних чисел ${\displaystyle {1 \over 2}+it}$, де ${\displaystyle t}$ — дійсне число, а ${\displaystyle i}$ — уявна одиниця.

Сформулював гіпротезу Бернгард Ріман 1859 року.

Особливе значення гіпотези Рімана полягає в (імовірному) взаємозв'язку малюнка розподілу на критичній прямій нетривіальних нулів дзета-функції Рімана з асимптотикою розподілу простих чисел. Це питання має значення як для чистої математики (в теорії чисел), так і дял прикладної математики (наприклад, для криптографії). Хоча не було знайдено ніякої закономірності у розподілі простих чисел серед натуральних, Ріман виявив, що кількість простих чисел, які не перевищують ${\displaystyle x}$, — функція розподілу простих чисел ${\displaystyle \pi (x)}$ — виражається через розподіл нетривіальних нулів дзета-функції. Гіпотеза стала основою подальшого доведення Адамаром і Валле-Пуссеном (1896) теореми про розподіл простих чисел.

Також було висунуто гіпотези про можливий зв'язок статистичних властивостей нетривіальних нулів дзета-функції Рімана (а отже й простих чисел) із явищами квантової фізики, зокрема з квантовим хаосом.

Гіпотезу Рімана часто розглядають як найважливішу нерозв'язану математичну проблему.^[1][2][3] Сама гіпотеза, разом із гіпотезою Ґольдбаха, становлять восьму проблему Гільберта — одну з небагатьох недоведених станом на 2023 рік проблем Гільберта. Також гіпотеза Рімана — єдина з проблем Гільберта, включена 2000 року до списку семи «Проблем тисячоліття», за розв'язання кожної з яких Математичний інститут Клея обіцяє нагороду в 1 млн доларів США. Попри безліч спроб (періодично публікованих) дослідження гіпотези, жодну з них так і не визнала наукова спільнота.^[4]

Існує багато математичних проблем, доведених у припущенні істинності гіпотези Рімана, так що її доведення чи спростування буде мати далекосяжні наслідки для теорії чисел, особливо в галузі розподілу простих чисел.^[5][6]

На 2004 рік чисельними методами підтверджено, що більше 10¹³ (десяти трильйонів) перших нетривіальних нулів дзета-функції Рімана задовольняють цю гіпотезу, що є добрим аргументом на користь її істинності, але не гарантує її.

Формулювання

Дійсна (червона) та уявна (синя) компоненти дзета-функції

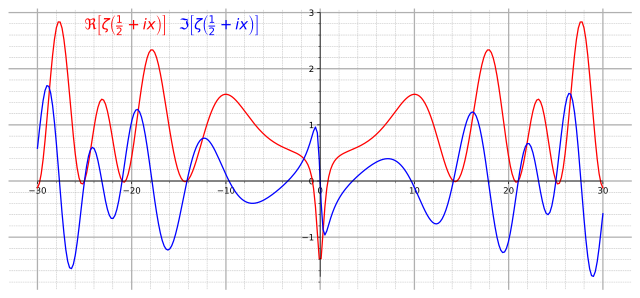
Гіпотеза стверджує, що:

Дійсна частина всіх нетривіальних нулів дзета-функції ${\displaystyle \zeta (s)}$ дорівнює ${\displaystyle {1 \over 2}}$

Функція ${\displaystyle \zeta (s)}$ визначена для всіх комплексних ${\displaystyle s\neq 1}$, і має нулі для від'ємних цілих ${\displaystyle s=-2,-4,-6\dots }$. Із функціонального рівняння ${\displaystyle \zeta (s)=2^{s}\pi ^{s-1}\sin {\pi s \over 2}\Gamma (1-s)\zeta (1-s)}$, і явного виразу ${\displaystyle {\frac {1}{\zeta (s)}}=\sum _{n=1}^{\infty }{\frac {\mu (n)}{n^{s}}}}$ при ${\displaystyle \operatorname {Re} \,s>1}$ випливає, що всі інші нулі, які називаються «нетривіальними», розташовані у смузі ${\displaystyle 0\leqslant \operatorname {Re} \,s\leqslant 1}$ симетрично відносно так званої «критичної лінії» ${\displaystyle {1 \over 2}+it,\;t\in \mathbb {R} }$.

Узагальнена гіпотеза Рімана

Узагальнена гіпотеза Рімана — аналог гіпотези Рімана для узагальнень дзета-функцій, званих L-функціями Діріхле.

Еквівалентні формулювання

Ріман виклав еквівалентне формулювання, яке свідчить, що всі корені ксі-функції Рімана^[en] ξ(s) дійні.

1901 року Гельге фон Кох показав, що гіпотеза Рімана еквівалентна такому твердженню про розподіл простих чисел:

${\displaystyle \pi (x)=\int \limits _{2}^{x}\!{\frac {dt}{\ln t}}+O\left({\sqrt {x}}\ln x\right)}$ при ${\displaystyle x\rightarrow \infty .}$

Ще кілька еквівалентних формулювань:

• Для всіх ${\displaystyle x\geqslant 2657}$ виконується нерівність ${\displaystyle \left|\pi (x)-\int \limits _{2}^{x}\!{\frac {dt}{\ln t}}\right|<{\frac {1}{8\pi }}{\sqrt {x}}\,\ln x,}$
• Для всіх ${\displaystyle x\geqslant 73{,}2}$ виконується нерівність ${\displaystyle |\psi (x)-x|<{\frac {1}{8\pi }}{\sqrt {x}}\,\ln ^{2}(x),}$ где ψ(x) — друга функція Чебишова^[en],
• Для всіх ${\displaystyle n>5040}$ виконується нерівність ${\displaystyle \sigma (n)<e^{\gamma }n\log \log n,}$ де ${\displaystyle \sigma (n)}$ — сума дільників числа ${\displaystyle n}$, а ${\displaystyle \gamma }$ — стала Ейлера-Маскероні. Нерівність порушується при n = 5040 і деяких менших значеннях (всього 27 винятків), але Гай Робін 1984 року показав, що вона виконується для всіх більших цілих чисел, тоді й лише тоді, коли виконується гіпотеза Рімана, і що послідовність винятків з умови теореми Робіна нескінченно довга, якщо гіпотеза Рімана хибна. Відомо також, що найменше з таких чисел-винятків n ≥ 5041 має бути супернадлишковим числом^[en].
• Для всіх ${\displaystyle n>1}$ виконується нерівність ${\displaystyle \sigma (n)<H_{n}+e^{H_{n}}\ln H_{n},}$ де ${\displaystyle H_{n}}$ — ${\displaystyle n}$-не гармонічне число.^[7]
• Для будь-якого додатного ${\displaystyle \varepsilon }$ виконується нерівність ${\displaystyle M(n)=O(n^{1/2+\varepsilon })}$, де ${\displaystyle M(n)}$ — функція Мертенса, див. також позначення O велике. Сильнішу гіпотезу ${\displaystyle |M(n)|<{\sqrt {n}}}$ спростовано 1985 року^[8].
• Гіпотеза Рімана еквівалентна такій рівності: ${\displaystyle \int \limits _{0}^{\infty }{\frac {(1-12t^{2})}{(1+4t^{2})^{3}}}\int \limits _{1/2}^{\infty }\log |\zeta (\sigma +it)|\,d\sigma \,dt={\frac {\pi (3-\gamma )}{32}}}$.
• Показано, що гіпотеза Рімана істинна тоді й лише тоді, коли інтегральне рівняння

${\displaystyle \int _{0}^{\infty }{\frac {z^{-\sigma -1}\phi (z)\,dz}{{e^{x/z}}+1}}=0}$

не має нетривіальних розв'язків ${\displaystyle \phi }$ для ${\displaystyle 1/2<\sigma <1}$.

Історія

1896 року Адамар і Валле-Пуссен незалежно довели, що нулі дзета-функції не можуть лежати на прямих ${\displaystyle \operatorname {Re} \,s=0}$ і ${\displaystyle \operatorname {Re} \,s=1}$.

1900 року Давид Гільберт включив гіпотезу Рімана до списку 23 нерозв'язаних проблем як частину восьмої проблеми, разом із гіпотезою Ґольдбаха.

1914 року Ґодфрі Гарольд Гарді довів, що на критичній лінії лежить нескінченно багато нулів, а пізніше Гарді і Літлвуд дали оцінку знизу частки нулів, що лежать на критичній лінії, яку потім покращували різні математики.

Деякі нетривіальні нулі розташовуються екстремально близько один від одного. Ця властивість відома як «Лемерове явище^[en]» (Деррік Лемер^[en]).

Титчмарш і Ворос 1987 року довели, що дзета-функцію можна розкласти в добуток через її нетривіальні нулі (розклад Адамара).

2004 року група математиків університету Пердью під керівництвом Луї де Бранжа^[en] запропонувала доведення гіпотези Рімана^[9], яке, однак, виявилося помилковим^[10].

Чергове повідомлення про доведення гіпотези Рімана надійшло 2018 року від математика Майкла Атії. Це відбулося під час конференції Heidelberg Laureate Forum в Гейдельберзькому університеті.^[11]

Цікаві факти

• Знаменита відповідь Гільберта на питання про те, що б він зробив, якби він з якої-небудь причини заснув на п'ятсот років і раптом прокинувся. Математик відповів, що в першу чергу він запитає, чи доведено гіпотезу Рімана.
• 2015 року прес-служба Математичного інституту Клея повідомила, що нігерійський математик Опіємі Енох із Федерального університету в м. Оє-Екіті зумів довести гіпотезу Рімана. Разом з тим, у Математичному інституті Клея заявили, що досягнення буде зафіксовано тільки після його публікації в міжнародному журналі з високою репутацією, тобто після верифікації науковою спільнотою.^[12]