Деформація згину

Деформа́ція зги́ну або згин — тип деформації бруса (балки), що полягає у викривленні осі прямого бруса чи зміні кривини осі кривого бруса внаслідок виникнення в його перерізах згинальних моментів від прикладених навантажень (поперечних сил і / або згинальних моментів у площині, що проходить через вісь бруса).

Деформація згину
Формула	${\displaystyle {\cfrac {\mathrm {d} ^{2}w(x)}{\mathrm {d} x^{2}}}={\frac {M(x)}{E(x)I(x)}}}$
Частково збігається з	стійкість
Деформація згину у Вікісховищі

Згин двотавра

Схематичне зображення деформації згину навантаженої балки

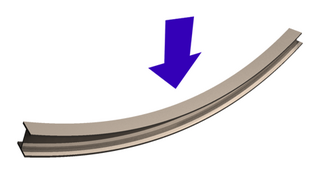
Локальна деформація різних частин тіла при згинанні різна. Наприклад, у випадку, зображеному на рисунку, верхня частина балки стискається, а нижня — розтягується.

Прямий згин балки виникає в разі, коли згинальний момент у поперечному перерізі бруса діє у площині, яка проходить через одну з головних центральних осей інерції цього перерізу. Якщо ж площина дії згинального моменту в даному поперечному перерізі бруса не проходить через жодну з головних осей інерції цього перерізу, згин називають косим.

Основні поняття

Переміщення будь-якої точки осі балки, котра працює на згин, виражається вектором, початок якого суміщено з початковим положенням точки, а кінець — з положенням цієї самої точки у деформованій балці. У прямих балках переміщення точок, спрямовані перпендикулярно до початкового положення осі, називають прогинами і позначають ${\displaystyle w(x)}$. При згинанні відбувається також поворот перерізів балки навколо осей, що лежать у площинах перерізів, який позначають ${\displaystyle \theta (x)}$.

Криву, що її форми набуває вісь балки (бруса) під час згину в межах пружної деформації називають пружна лінія.

Види згину

Стосовно бруса розрізняють згин плоский, або простий, та складний. При плоскому (простому) згині зовнішні сили діють в одній з головних площин бруса (вони проходять через вісь бруса і головні осі інерції поперечного перерізу, див. Моменти інерції плоских перерізів), при складному згині — в різних площинах. Різновидом складного є косий згин, коли навантаження діють у площині, що не збігається з жодною з головних площин.

Залежно від сил, що діють у поперечному перерізі бруса, згин буває чистим (за наявності лише згинальних моментів), поперечним (діють поперечні сили), поздовжнім (випинання під впливом стискувальних сил, спрямованих уздовж осі) і поперечно-поздовжнім.

Розрахунки при згині

Елемент балки, вирізаний двома суміжними поперечними перерізами, у здеформованому стані

Класична теорія

Наближений розрахунок прямого бруса на дію згину у пружній стадії на основі класичної теорії (теорії Ейлера — Бернуллі) проводиться, виходячи з таких допущень:

• поперечні перерізи, що були плоскими й перпендикулярними до осі балки до деформування, залишаються плоскими і перпендикулярними до її зігнутої осі (пружної лінії) після деформування (гіпотеза плоских перерізів);
• поздовжні волокна бруса при згині не тиснуть одне на інше і не намагаються відірватись одне від одного;
• переміщення і деформації вважаються малими, а балка — нерозтяжною;
• розміри перерізів балки вважаються малими, порівняно з радіусом кривини осі балки;
• матеріал балки розглядається як лінійно пружний, що описується законом Гука.

За плоского згину, в будь-якій точці поперечного перерізу балки виникають нормальні (σ) і дотичні (τ) напруження. Нормальні напруження визначають за формулою Нав'є:

${\displaystyle \sigma =E\varepsilon =E{\frac {y}{\rho }}={\frac {M_{z}y}{I_{z}}},}$

де: M_z — згинальний момент;

y — координата досліджуваної точки відносно нейтральної лінії;

I_z — момент інерції відносно нейтральної лінії.

Дотичні напруження визначають за формулою Д. І. Журавського:

${\displaystyle \tau ={\frac {Q_{y}S_{z}}{bI_{z}}},}$

де Q_y — поперечна сила у перерізі;

S_z — статичний момент відносно нейтральної осі частини площі поперечного перерізу, розташованої вище (або нижче) від волокна, що розглядається;

_b — ширина перерізу на рівні волокна, що розглядається.

Характер зміни згинальних моментів і поперечних сил за довжиною бруса зазвичай зображують графіками (епюрами), за якими визначають їх розрахункові значення.

Ступінь викривлення осі в межах пружності залежить від величини згинального моменту і жорсткості бруса. Кривина осі визначається виразом:

${\displaystyle {\frac {1}{\rho }}={\frac {M_{z}}{EI_{z}}},}$

де ρ — радіус кривини осі зігнутого бруса в розглянутому перерізі; Е — модуль Юнга матеріалу бруса, I_z — момент інерції. Добуток EI_z називають жорсткістю балки на згин.^[1]

Для випадку малих деформацій кривина наближено виражається другою похідною від прогину ${\displaystyle w(x)}$, тому між координатами зігнутої осі та згинальним моментом існує диференціальна залежність:

${\displaystyle {\frac {d^{2}w(x)}{dx^{2}}}={\frac {M_{z}}{EI_{z}}},}$

що називається диференціальним рівнянням осі зігнутого бруса. Його розв'язок називають рівнянням пружної лінії балки (бруса).

Відносна деформація під час згину визначається як: ε${\displaystyle ={\frac {y}{\rho }}}$, ε${\displaystyle _{max}={\frac {h/2}{\rho }}}$, де h — висота балки.

У практичних дослідах на згин для визначення відносної деформації ε вимірюють прогини зразків. Взаємозв'язок між прогином f, що вимірюється між внутрішніми роликами, розташованими на відстані l₀, за чотириточковим (круговим) згином та радіусом кривини ρ такий:

${\displaystyle \rho ={\frac {l_{0}^{2}}{8f}}}$.

Тоді ε${\displaystyle _{4t}=f{\frac {4h}{l_{0}^{2}}}}$. Для триточкового згину ця формула буде такою: ε${\displaystyle _{3t}=f{\frac {6h}{l_{0}^{2}}}}$.

Теорія балки Тимошенка

Докладніше: Теорія балки Тимошенка

Ця теорія базується на тих самих гіпотезах, що й класична, однак гіпотезу плоских перерізів модифіковано: приймається, що перерізи, які були до деформації плоскими і нормальними до осі балки, залишаються плоскими, але перестають бути нормальними до зігнутої осі. Таким чином, ця теорія враховує деформацію зсуву й дотичні напруження. Врахування дотичних напружень важливе для композитів та матеріалів, що мають шарувату структуру (деревина), оскільки руйнування може відбуватися внаслідок зсуву уздовж лінії розмежування шарів.

Основні залежності:

${\displaystyle M_{z}=EI_{z}{\frac {\,d\theta (x)}{\,dx}}}$

${\displaystyle Q_{y}={\frac {GF}{\alpha }}\left(\theta (x)-{\frac {\,dw(x)}{\,dx}}\right)}$

де ${\displaystyle G}$ — модуль зсуву матеріалу балки, ${\displaystyle F}$ — площа перерізу, ${\displaystyle \alpha }$ — коефіцієнт, що враховує нерівномірність розподілу дотичних напружень у перерізі та залежить від його форми. Величина

${\displaystyle \gamma =\theta (x)-{\frac {\,dw(x)}{\,dx}}}$

— це кут зсуву.

Згин балок на пружній основі

Цією розрахунковою схемою моделюють залізничні рейки, а також кораблі (в першому наближенні).

Пружна основа розглядається як множина не пов'язаних між собою пружинок.

Найпростіший метод розрахунку ґрунтується на гіпотезі Вінклера: реакція пружної основи пропорційна прогину в точці і напрямлена назустріч йому:

${\displaystyle p=-k\cdot v}$

де ${\displaystyle v}$ — прогин;

${\displaystyle p}$ — реакція (на одиницю довжини балки);

${\displaystyle k}$ — коефіцієнт пропорційності (називаний коефіцієнтом постелі).

При цьому основу вважають двобічною, тобто, реакція виникає як при втисканні балки в основу, так і при її відриві від основи. Гіпотеза Бернуллі зберігається.

Диференціальне рівняння згину балки на пружній основі має вигляд:

${\displaystyle {\frac {d^{2}}{dz^{2}}}\left(EJ_{x}(z){\frac {d^{2}v}{dz^{2}}}\right)+k(z)\cdot v=q(z)}$

де ${\displaystyle v(z)}$ — прогин;

${\displaystyle EJ_{x}(z)}$ — згинальна жорсткість (може бути змінною за довжиною);

${\displaystyle k(z)}$ — змінний за довжиною коефіцієнт постелі;

${\displaystyle q(z)}$ — розподілене навантаження на балку.

За постійних жорсткості і коефіцієнті постелі рівняння можна записати у вигляді:

${\displaystyle EJ_{x}{\frac {d^{4}v}{dz^{4}}}+k\cdot v=q(z)}$

або

${\displaystyle {\frac {d^{4}v}{dz^{4}}}+4m^{4}\cdot v=q(z)}$

де позначено

${\displaystyle 4m^{4}={\frac {k}{EJ_{x}}}}$

Згин бруса великої кривини

Для балок, радіус кривини осі яких ${\displaystyle \rho _{0}}$ порівнянний з висотою перерізу ${\displaystyle h}$, тобто:

${\displaystyle {\frac {h}{\rho _{0}}}>0,2}$

розподіл напружень за висотою відхиляється від лінійного, а нейтральна лінія не збігається з віссю перерізу (яка проходить через центр тяжіння перерізу). Така розрахункова схема використовується, наприклад, для розрахунку ланок ланцюгів та гаків^[ru] підйомних кранів.

Поперечний переріз

Формула для розподілу напружень має вигляд:

${\displaystyle \sigma ={\frac {M}{F\cdot e}}\cdot {\frac {y}{R+y}}}$

де ${\displaystyle M}$ — згинальний момент у перерізі;

${\displaystyle R}$ — радіус нейтральної лінії перерізу;

${\displaystyle F}$ — площа перерізу;

${\displaystyle e=R_{0}-R}$ — ексцентриситет;

${\displaystyle y}$ — координата за висотою перерізу, відлічувана від нейтральної лінії.

Радіус нейтральної лінії визначається за формулою:

${\displaystyle R=\int {\frac {\,dF}{u}}=\int \limits _{R_{1}}^{R_{2}}{\frac {b(u)\,du}{u}}}$

Інтеграл береться за площею перерізу, координата ${\displaystyle u}$ відлічується від центра кривини. Справедливі також наближені формули:

${\displaystyle e={\frac {J_{x}}{R_{0}\cdot F}}}$

${\displaystyle r_{0}=R_{0}-{\frac {J_{x}}{R_{0}\cdot F}}}$

Для перерізів, що часто використовуються, є аналітичні формули. Для прямокутного перерізу заввишки ${\displaystyle h}$ :

${\displaystyle R={\frac {h}{\ln \displaystyle {\frac {R_{0}+{\frac {h}{2}}}{R_{0}-{\frac {h}{2}}}}}}={\frac {h}{\ln \displaystyle {\frac {R_{2}}{R_{1}}}}}}$

де ${\displaystyle R_{1},R_{2}}$ — радіуси кривини внутрішньої та зовнішньої поверхонь балки відповідно.

Для круглого перерізу:

${\displaystyle R={\frac {R_{0}+{\sqrt {R_{0}^{2}-r^{2}}}}{2}}}$

де ${\displaystyle r}$ — радіус перерізу.

Перевірка міцності балки

де ${\displaystyle \sigma _{b}}$ — межа міцності матеріалу балки, ${\displaystyle n_{b}}$ — коефіцієнт запасу за міцністю.

${\displaystyle \sigma _{max}<{\frac {\sigma _{T}}{n_{T}}}}$

де ${\displaystyle \sigma _{T}}$ — межа плинності матеріалу балки, ${\displaystyle n_{T}}$ — коефіцієнт запасу за плинністю. Для крихких матеріалів:

${\displaystyle \sigma _{max}<{\frac {\sigma _{b}}{n_{b}}}}$

де ${\displaystyle \sigma _{b}}$ — межа міцності матеріалу балки, ${\displaystyle n_{b}}$ — коефіцієнт запасу за міцністю.

У разі пластичних матеріалів ці формули можуть суттєво занижувати значення навантаження, за якого балка втрачає тримкість. Фактично тримкість втрачається лише тоді, коли в якомусь перерізі весь матеріал переходить у пластичний стан. Тоді в перерізі можуть виникати неприпустимі переміщення (утворюється так званий пластичний шарнір). Якщо за діаграму розтягу-стиску взяти діаграму Прандтля, то граничний згинальний момент ${\displaystyle M_{pr}}$ для стрижня прямокутного перерізу шириною ${\displaystyle b}$ та заввишки ${\displaystyle h}$ виражається формулою:

${\displaystyle M_{pr}={\frac {1}{4}}bh^{2}\sigma _{T}}$

Динамічне навантаження балок

Власні коливання

Розглянемо балку з густиною матеріалу ${\displaystyle \rho }$, площею поперечного перерізу ${\displaystyle A}$, згинальною жорсткістю ${\displaystyle EJ}$. Рівняння власних коливань має вигляд:

${\displaystyle {\frac {\partial ^{2}}{\partial z^{2}}}\left(EJ{\frac {\partial ^{2}x}{\partial z^{2}}}\right)+m_{0}{\frac {\partial ^{2}x}{\partial t^{2}}}=0}$

де ${\displaystyle x(z,t)}$ — поперечне переміщення, ${\displaystyle m_{0}=\rho A}$ — маса одиниці довжини стрижня. Розв'язок шукається у вигляді:

${\displaystyle x(z,t)=u(z)\cos(pt+\phi )}$

Підставляючи, отримуємо звичайне диференціальне рівняння:

${\displaystyle {\frac {d^{2}}{dz^{2}}}\left(EJ{\frac {d^{2}u}{dz^{2}}}\right)-m_{0}p^{2}u=0}$

Для балки постійного перерізу воно набуває вигляду:

${\displaystyle {\frac {d^{4}u}{dz^{4}}}-\alpha ^{4}u=0}$

де

${\displaystyle \alpha ^{4}={\frac {p^{2}m_{0}}{EJ}}}$

Зручно подати розв'язок, скориставшись функціями Крилова:

${\displaystyle u=\sum _{i=1}^{4}C_{i}K_{i}(\alpha z)}$

де функції Крилова:

${\displaystyle K_{1}(\alpha z)={\frac {1}{2}}(\operatorname {ch} \alpha z+\cos \alpha z)}$

${\displaystyle K_{2}(\alpha z)={\frac {1}{2}}(\operatorname {sh} \alpha z+\sin \alpha z)}$

${\displaystyle K_{3}(\alpha z)={\frac {1}{2}}(\operatorname {ch} \alpha z-\cos \alpha z)}$

${\displaystyle K_{4}(\alpha z)={\frac {1}{2}}(\operatorname {sh} \alpha z-\sin \alpha z)}$

а ${\displaystyle C_{i}}$ — сталі.

Функції Крилова пов'язані залежностями:

${\displaystyle {\frac {d}{dz}}K_{1}(\alpha z)=\alpha K_{4}(\alpha z)}$

${\displaystyle {\frac {d}{dz}}K_{2}(\alpha z)=\alpha K_{1}(\alpha z)}$

${\displaystyle {\frac {d}{dz}}K_{3}(\alpha z)=\alpha K_{2}(\alpha z)}$

${\displaystyle {\frac {d}{dz}}K_{4}(\alpha z)=\alpha K_{3}(\alpha z)}$

Ці залежності значно спрощують запис граничних умов для балок:

${\displaystyle C_{1}=u_{z=0};C_{2}={\frac {1}{\alpha }}\left({\frac {du}{dz}}\right)_{z=0};C_{3}={\frac {1}{EJ\alpha ^{2}}}M_{z=0};C_{4}={\frac {1}{EJ\alpha ^{3}}}Q_{z=0}}$

На кожному кінці балки задаються дві граничні умови.

Рівняння власних коливань має безліч розв'язків. Але практичний інтерес, зазвичай, становлять лише декілька перших, відповідні нижчим власним частотам.

Загальна формула для власної частоти має вигляд:

${\displaystyle p_{k}=\lambda _{k}^{2}{\sqrt {\frac {EJ}{m_{0}l^{4}}}}}$

Для однопрогінних балок:

Закріплення		${\displaystyle \lambda _{k}}$
Лівий кінець	Правий кінець
Закріплений	Закріплений	${\displaystyle \lambda _{1}=4,73;}$${\displaystyle \lambda _{2}=7,853;}$
Вільний	Вільний	${\displaystyle \lambda _{1}=0;}$${\displaystyle \lambda _{2}=0;}$ при k>2 ${\displaystyle \lambda _{k}={\frac {2k+1}{2}}\pi$ ;}
Закріплений	Шарнір	${\displaystyle \lambda _{1}=3,927;}$${\displaystyle \lambda _{2}=7,069;}$ при k>2 ${\displaystyle \lambda _{k}={\frac {4k+1}{4}}\pi$ ;}
Шарнір	Шарнір	${\displaystyle \lambda _{k}=k\pi }$
Закріплений	Вільний	${\displaystyle \lambda _{1}=1,875;}$${\displaystyle \lambda _{2}=4,694;}$ при k>2 ${\displaystyle \lambda _{k}={\frac {2k-1}{2}}\pi$ ;}

Див. також

• Поздовжній згин
• Випробування на згинання