Топ питань
Часова шкала
Чат
Перспективи
Зрізаний тетраедр
многогранник З Вікіпедії, вільної енциклопедії
Remove ads
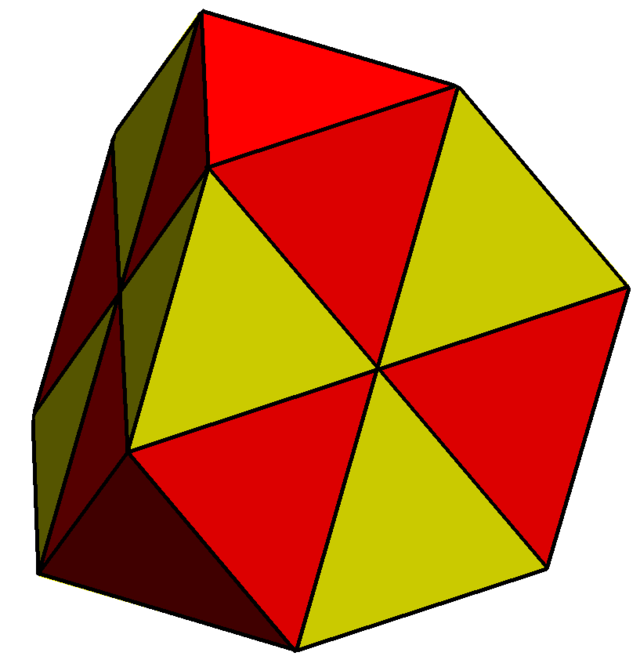
Зрі́заний тетра́едр — напівправильний многогранник, відноситься до архімедових тіл, що складається із 4 правильних шестикутників і 4 правильних трикутників. В кожній із 12 вершин сходяться дві шестикутні грані і один правильний трикутник. Кількість двотипних ребер налічує 18 штук. Двоїстий до зрізаного тетраедра многогранник — триакістетраедр.


Отримати даний многогранник можна за рахунок зрізання всіх чотирьох вершин правильного тетраедра на третину від первісної довжини ребра.
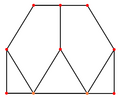
Ортогональні проєкції
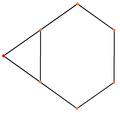
| 
| 
| 
|
Remove ads
Формули
Знаючи довжину ребра зрізаного тетраедра — a - отримуємо:
Remove ads
Графічне зображення
Якщо шестикутну грань зрізаного тетраедра розділити на трикутники із заданою довжиною ребра то дані трикутники будуть ідентичні правильним трикутникам самого зрізаного тетраедра.

Сферична плитка
Зрізаний тетраедр можна подати у вигляді сферичної плитки, і спроєктувати на площину у вигляді стереографічної проєкції. Ця проєкція буде конформною, зберігаючи кути, але не площини чи ребра многогранника. Прямі лінії на сфері проєктуватимуться як дуги на площині.
Джерела
- Weisstein, Eric W. Cuboctahedron(англ.) на сайті Wolfram MathWorld.
- Пчелінцев В. О. Кристалографія, кристалохімія та мінералогія. Навчальний посібник для студентів вищих навчальних закладів. Суми: Вид-во СумДУ, 2008, — 232с.
- Гордєєва Є. П., Величко В. Л. Нарисна геометрія. Багатогранники (правильні, напівправильні та зірчасті). Частина І. Навчальний посібник. Луцьк: Редакційно-видавничий відділ ЛДТУ, 2007, — 198с.
- П. С. Александрова, А. И. Маркушевича и А. Я. Хинчина. Многоугольники и многогранники. Энциклопедия элементарной математики. Москва: Государственное издательство физико-математической литературы, 1963, — 568с.
Remove ads
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads

 ,
,  ...
...