Розгортка многогранника

Розгортка многогранника — набір з'єднаних сторонами многокутників у площині, які можна зігнути (уздовж ребер) та склеїти вздовж межі, перетворивши на грані многогранника. Розгортки многогранників використовуються при вивченні многогранників і в стереометрії взагалі. Використовуючи розгортку многогранника легко виготовити просторову модель многогранника, наприклад, із картону.^[1]

Розгортка октаедра на площину

Розгортка додекаедра

Ще одна розгортка додекаедра

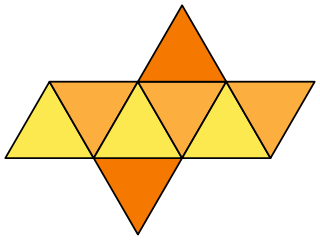
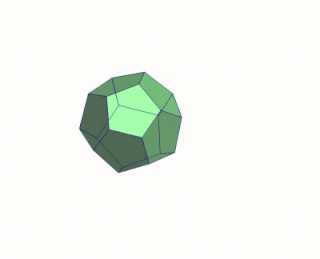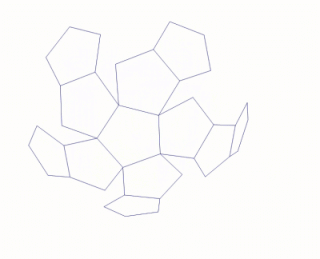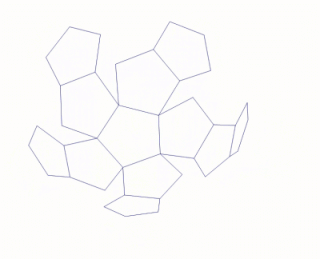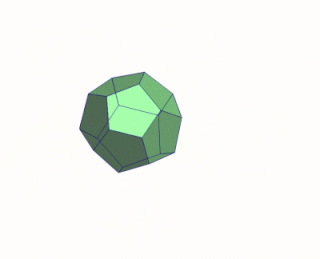
Нескладно побачити, що для одного й того ж многогранника можуть існувати різні розгортки.

Площа поверхні многогранника — це сума площ усіх його граней, вона дорівнює площі розгортки цього многогранника^[2].

Ранній приклад розгорток многогранників з'являється в роботах Альбрехта Дюрера, чия книга 1525 року «Курс мистецтва вимірювання циркулем і лінійкою» (Unterweysung der Messung mit dem Zyrkel und Rychtscheyd) містила розгортки платонових тіл і кількох архімедових тіл.^[3][4]

Існування та унікальність

Чотири шестикутники, які, склеєні для утворення правильного октаедра, як зображено, утворюють складки за трьома діагоналями кожного шестикутника. Ребра між шестикутниками залишаються без складок.

Для заданого многогранника може існувати багато різних розгорток, залежно від вибору того, за якими ребрами виконується розділення. Ребра, вздовж яких опуклий многогранник розрізають для формування розгортки, мають утворювати кісткове дерево многогранника, але розрізання за деякими кістяковими деревами може під час розгортання призвести до самоперекриття, а не до формування розгортки.^[5] І навпаки, задана розгортка може складатися в більш ніж один опуклий многогранник, залежно від кутів, під якими складаються її ребра, та вибору ребер для склеювання.^[6] Якщо задано розгортку разом зі шаблоном для склеювання її ребер, так, що кожна вершина кінцевої форми має додатний кутовий дефект і сума цих дефектів дорівнює 4π, то обов'язково існує рівно один многогранник, який можна скласти з неї (теорема єдиності Александрова). Однак, многогранник, сформований у такий спосіб, може мати інші грані, ніж зазначені як частина розгортки: деякі многокутники розгортки можуть мати згини, а деякі ребра між многокутниками розгортки можуть залишитися розгорнутими. Крім того, одна й та сама розгортка може мати кілька допустимих варіантів склеювання, що приводить до складання різних многогранників.^[7]

Нерозв'язана проблема математики: Чи кожен опуклий многогранник має просту розгортку за ребрами? (більше нерозв'язаних проблем математики)

1975 року Дж. К. Шепард^[en] запитав, чи кожен опуклий многогранник має хоча б одну розгортку або просту розгортку за ребрами.^[8] Це питання, також відоме як гіпотеза Дюрера або проблема розгортання Дюрера, залишається без відповіді.^[9][10][11] Існують неопуклі многогранники, які не мають розгорток, і можна розділити грані кожного опуклого многогранника (наприклад, уздовж множини розділення^[en]) так, щоб множина відділених граней мала розгортку.^[5] 2014 року Мохаммад Ґгомі (Mohammad Ghomi) показав, що кожен опуклий многогранник допускає розгортку після афінного перетворення.^[12] Крім того, 2019 року Барвінок та Ґгомі показали, що узагальнення гіпотези Дюрера не працює для псевдоребер,^[13] тобто мережі геодезичних, які з'єднують вершини многогранника та утворюють граф із опуклими гранями.

Пов'язане відкрите питання полягає в тому, чи кожна розгортка опуклого многогранника має розквітання^{[en][уточнити]} — неперервний рух без самоперетинів від плоского до складеного стану, протягом якого кожна грань залишається плоскою.^[14]

Найкоротший шлях

Найкоротший шлях поверхнею між двома точками на поверхні многогранника відповідає відрізку прямої на відповідній розгортці підмножини граней, якими проходить шлях. Розгортка має бути такою, щоб відрізок повністю містився в ній, і, можливо, доведеться розглянути кілька розгорток, щоб побачити, яка з них дає найкоротший шлях. Наприклад, у випадку куба, якщо точки лежать на суміжних гранях, одним із кандидатів на найкоротший шлях є шлях, що перетинає спільне ребро; найкоротший шлях такого типу знаходимо за допомогою розгортки, де ці дві грані також є суміжними. Інші кандидати на найкоротший шлях проходять через поверхню третьої грані, що прилягає до обох (яких дві), і, використавши відповідні розгортки, можна знайти найкоротший шлях у кожному випадку.^[15]

Задача про павука та муху — розважальна математична головоломка, яка полягає в пошуку найкоротшого шляху між двома точками на прямокутному паралелепіпеді.

Розгортки у просторах вищих вимірів

Геометричну концепцію розгорток можна узагальнити на простори вищих вимірів.

Розгортка 4-політопа (чотиривимірного многогранника), складається з комірок-многогранників, які з'єднані своїми гранями та всі лежать в одному тривимірному просторі, так само як многокутники розгортки многогранника з'єднані своїми ребрами та всі лежать в одній площині. Розгортку тесеракта, чотиривимірного гіперкуба, використав Сальвадор Далі на картині «Розп'яття або Гіперкубічне тіло» (1954).^[16] Також вона є центром сюжету оповідання Роберта Гайнлайна «І побудував він будинок».^[17]

Кількість комбінаторно різних розгорток ${\displaystyle n}$-вимірного гіперкуба можна знайти, подавши розгортку як дерево з ${\displaystyle 2n}$ вузлів, яке описує, як пари граней гіперкуба склеюються разом, утворюючи розгортку, разом з досконалим паруванням на доповненні дерева, що описує пари граней, розташовані одна навпроти одної на складеному гіперкубі. Використовуючи це подання, підраховано, що кількість різних розгорток для гіперкубів у розмірностіх 2, 3, 4, … становить

1, 11, 261, 9694, 502110, 33064966, 2642657228, … послідовність A091159 з Онлайн енциклопедії послідовностей цілих чисел, OEIS

На зображеннях наведено розгортки деяких 4-політопів.

4-куб

Зрізаний тесеракт

Ікосітетрахорон

Див. також

• Згинаний многогранник
• Патерн оригамі
• Паперове моделювання
• Спільна розгортка
• UV mapping