Топ питань
Часова шкала
Чат
Перспективи
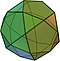
Архімедове тіло
високо симетричний напівправильний опуклий багатогранник, гранями якого є два або більше типів правильних багатокутників, що примикають З Вікіпедії, вільної енциклопедії
Remove ads
В геометрії архімедове тіло (архімедів многогранник) — це високо симетричний напівправильний опуклий многогранник, гранями якого є два або більше типів правильних многокутників, що примикають до ідентичних вершин. Вони відрізняються від платонових тіл (правильних многогранників), які складаються тільки з одного типу многокутників в однакових вершинах, і від многогранників Джонсона, правильні многокутні грані яких належать різним типам вершин.
Ромбозрізаний ікосододекаедр є найбільшим архімедовим тілом за об'ємом (для одиничної довжини ребра), а також з найбільшою кількістю вершин і ребер.
Псевдоромбокубооктаедр має одну вершинну фігуру, 3.4.4.4, але з поворотом одного квадратного купола. На відміну від (не повернутого) ромбокубооктаедра, фігура не є вершинно-транзитивною.
Тут поняття «ідентичні вершини» означає, що для будь-яких двох вершин існує ізометрія всього тіла, яка переводить одну вершину в іншу. Іноді тільки потрібно, щоб грані, прилеглі до однієї вершини, були ізометричними граням при іншій вершині. Ця різниця в термінах визначає, вважається подовжений квадратний гіробікупол[ru] (псевдоромбокубооктаедр) архімедовим тілом чи многогранником Джонсона — це єдиний опуклий многогранник, в якому многокутні межі примикають до вершини однаковим способом у кожній вершині, але многогранник не має глобальної симетрії, яка б переводила будь-яку вершину в будь-яку іншу. Ґрунтуючись на існуванні псевдоромбокубооктаедра, Ґрюнбаум[1] запропонував термінологічну відмінність, у якій архімедове тіло визначається як таке, що має одну і ту ж вершинну фігуру в кожній вершині (включно з подовженим квадратним гіробікуполом), тоді як однорідний многогранник визначається як тіло, у якого будь-яка вершина симетрична будь-який інший (що виключає гіробікупол[ru]).
Призми і антипризми, групами симетрій яких є діедричні групи, як правило, не вважаються архімедовим тілами, незважаючи на те, що вони підпадають під визначення, дане вище. З цим обмеженням існує тільки скінченне число архімедових тіл. Всі тіла, крім подовженого квадратного гіробікупола, можна отримати побудовами Вітгоффа з платонових тіл за допомогою тетраедричної, октаедричної[en] і ікосаедричної[ru] симетрій.
Remove ads
Походження назви
Архімедові тіла отримали назву на честь Архімеда, який обговорював їх у нині втраченій роботі. Папп посилається на цю роботу і стверджує, що Архімед перелічив 13 многогранників[1]. За часів Відродження художники і математики цінували чисті форми і перевідкрити їх усі. Ці дослідження були майже повністю закінчені близько 1620 року Йоганном Кеплером[2], який визначив поняття призм, антипризм і неопуклих тіл, відомих як тіла Кеплера - Пуансо.
Кеплер, можливо, знайшов також подовжений квадратний гіробікупол (псевдоромбоікосаедр) — щонайменше, він стверджував, що є 14 архімедових тіл. Однак його опубліковані переліки включають тільки 13 однорідних многогранників, і перше ясне твердження про існування псевдоромбоікосаедра зробив 1905 року Дункан Соммервіль[1].
Remove ads
Класифікація
Узагальнити
Перспектива
Існує 13 архімедових тіл (не рахуючи подовженого квадратного гіробікупола; 15, якщо враховувати дзеркальні відображення двох енантіоморфів, які нижче перелічені окремо).
Тут вершинна конфігурація відноситься до типів правильних многокутників, які примикають до вершини. Наприклад, вершинна конфігурація (4,6,8) означає, що квадрат, шестикутник і восьмикутник зустрічаються у вершині (порядок переліку береться за годинниковою стрілкою відносно вершини).
Деякі визначення напівправильних многогранників включають ще одне тіло — подовжений квадратний гіробікупол або «псевдоромбокубооктаедр»[3].
Remove ads
Властивості
Число вершин дорівнює відношенню 720° до кутового дефекту при вершині.
Кубоктаедр і ікосододекаедр є реберно-однорідними і називаються квазіправильними[ru].
Дуальні многогранники архімедових тіл називаються каталановими тілами. Разом з біпірамідами і трапецоедрами вони є гране-однорідними тілами з правильними вершинами.
Хіральність
Кирпатий куб і кирпатий додекаедр хіральні, оскільки вони з'являються в лівосторонньому і правосторонньому варіантах. Якщо щось має кілька видів, які є тривимірним дзеркальним відображенням один одного, ці форми називають енантіоморфами (ця назва застосовується також для деяких форм хімічних сполук).
Побудова архімедових тіл
Узагальнити
Перспектива

Різні архімедові і платонові тіла можуть бути отримані одне з одного за допомогою декількох операцій. Починаючи з платонових тіл, можна використовувати операцію зрізання кутів. Для збереження симетрії зрізання виконується площиною, перпендикулярною до прямої, що з'єднує кут з центром многокутника. Залежно від того, наскільки глибоко виконується зрізання (див. таблицю нижче), отримаємо різні платонові і архімедові (й інші) тіла. Розширення[ru] або скошування[ru] здійснюється шляхом руху граней у напрямку від центра (на однакову відстань, щоб зберегти симетрію) і створенням, потім, опуклої оболонки. Розширення з поворотом здійснюється також обертанням граней, це ламає прямокутники, що виникають на місцях ребер, на трикутники. Остання побудова, яке ми тут розглянемо, це зрізання як кутів, так і ребер. Якщо нехтувати масштабування, розширення можна також розглядати як зрізання кутів і ребер, але з певним відношенням між зрізаннями кутів і ребер.
Зауважимо двоїстість між кубом і октаедром і між додекаедром і ікосаедром. Також, частково внаслідок самодвоїстості тетраедра, тільки одне архімедове тіло має тільки одну тетраедричну симетрію.
Remove ads
Див. також
Примітки
Література
Посилання
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads