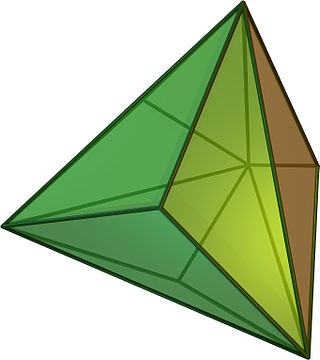
Триакістетраедр

Триакістетраедр (від дав.-гр. τριάχις — «тричі», τέτταρες — «чотири» і ἕδρα — «грань»), також званий тригон-тритетраедром, — напівправильний многогранник (каталанове тіло), двоїстий зрізаному тетраедру. Складений із 12 однакових тупокутних рівнобедрених трикутників, у яких один із кутів дорівнює ${\displaystyle \arccos \left(-{\frac {7}{18}}\right)\approx 112{,}89^{\circ },}$ а два інші — ${\displaystyle \arccos \,{\frac {5}{6}}\approx 33{,}56^{\circ }.}$

Триакістетраедр
Тип	каталанове тіло
Граней	12
Ребер	18
Вершин	8
Конфігурація вершин	4(33) 4(36)
Діаграма Коксетера
Група симетрії	Td (тетраедрична)
Двогранний кут (градуси)	129°31′16″ arccos(−7/11)
Дуальний многогранник	зрізаний тетраедр
опуклий, ізоедричний
Розгортка

Має 8 вершин; у 4 вершинах (розташованих так само, як вершини правильного тетраедра) сходяться своїми гострими кутами по 6 граней, у 4 вершинах (розташованих так само, як вершини іншого правильного тетраедра) сходяться тупими кутами по 3 грані.

У триакістетраедра 18 ребер — 6 «довгих» (розташованих так само, як ребра правильного тетраедра) і 12 «коротких». Двогранний кут при будь-якому ребрі дорівнює ${\displaystyle \arccos \left(-{\frac {7}{11}}\right)\approx 129{,}52^{\circ }.}$

Триакістетраедр можна отримати з правильного тетраедра, приклавши до кожної його грані правильну трикутну піраміду з основою, що дорівнює грані тетраедра, і висотою, яка в ${\displaystyle {\frac {5{\sqrt {6}}}{2}}\approx 6{,}12}$ разів менша від сторони основи. При цьому отриманий многогранник матиме по 3 грані замість кожної з 4 граней початкового — з чим і пов'язана його назва.

Метричні характеристики

Якщо «короткі» ребра триакістетраедра мають довжину ${\displaystyle a}$, то його «довгі» ребра мають довжину. ${\displaystyle {\frac {5}{3}}a\approx 1{,}67a,}$ а площа поверхні та об'єм виражаються як

${\displaystyle S={\frac {5{\sqrt {11}}}{3}}a^{2}\approx 5{,}5277080a^{2},}$

${\displaystyle V={\frac {25{\sqrt {2}}}{36}}a^{3}\approx 0{,}9820928a^{3}.}$

Радіус вписаної сфери (що дотикається до всіх граней многогранника в їхніх інцентрах) при цьому дорівнює

${\displaystyle r={\frac {5{\sqrt {22}}}{44}}a\approx 0{,}5330018a,}$

радіус напіввписаної сфери (що дотикається до всіх ребер)

${\displaystyle \rho ={\frac {5{\sqrt {2}}}{12}}a\approx 0{,}5892557a.}$

Описати навколо триакістетраедра сферу — так, щоб вона проходила через усі вершини, — неможливо.

Посилання

• Weisstein, Eric W. Триакістетраедр(англ.) на сайті Wolfram MathWorld.