Рівномірна неперервність

Рівномірна неперервність в математичному і функціональному аналізі — це властивість функції бути однаково неперервною в усіх точках області визначення.

Графік ${\displaystyle f(x)={\frac {1}{x}}}$ перетинає горішню і долішню риски обмежувального вікна висота × широта=${\displaystyle 2\varepsilon \times 2\delta ,}$ якою маленькою не була б ${\displaystyle \delta }$, отже ${\displaystyle f(x)}$ не рівномірно неперервна. Тоді як, функція ${\displaystyle g(x)={\sqrt {x}}}$ рівномірно неперервна.

Означення

Нехай дано два метричні простори ${\displaystyle (X,\varrho _{X})}$ і ${\displaystyle (Y,\varrho _{Y})}$. Функція ${\displaystyle f\colon X\to Y}$ називається рівномірно неперервною на підмножині ${\displaystyle M\subset X,}$ якщо

${\displaystyle \forall \varepsilon >0\;\exists \delta =\delta (\varepsilon )>0\;\forall x_{1},x_{2}\in M\quad {\bigl (}\varrho _{X}(x_{1},x_{2})<\delta {\bigr )}\Rightarrow {\bigl (}\varrho _{Y}(f(x_{1}),f(x_{2}))<\varepsilon {\bigr )}}$.

Зокрема, дійснозначна функція дійсного змінного ${\displaystyle f:M\subset \mathbb {R} \to \mathbb {R} }$ рівномірно неперервна, якщо

${\displaystyle \forall \varepsilon >0\;\exists \delta =\delta (\varepsilon )>0\;\forall x_{1},x_{2}\in M\quad {\bigl (}|x_{1}-x_{2}|<\delta {\bigr )}\Rightarrow {\bigl (}|f(x_{1})-f(x_{2})|<\varepsilon {\bigr )}}$

Вибір ${\displaystyle \delta }$ у визначенні рівномірної неперервності залежить від ${\displaystyle \varepsilon }$, але не від ${\displaystyle x_{1},x_{2}.}$

Властивості

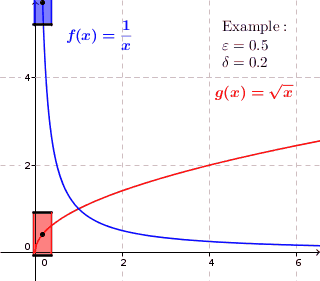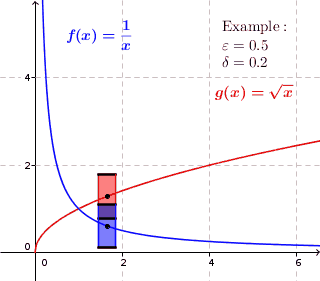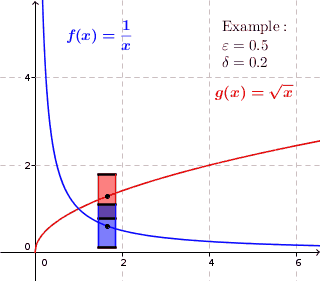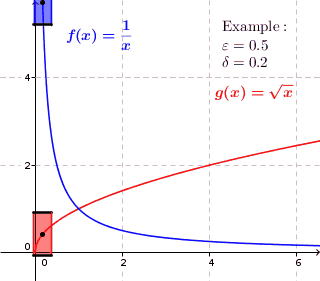
• Функція, рівномірно неперервна на множині ${\displaystyle M,}$ неперервна на ній. Зворотне, взагалі кажучи, не справджується. Наприклад, функція

${\displaystyle f(x)={\frac {1}{x}},\;x\in (0,1)}$

неперервна на всій області визначення, але не є рівномірно неперервною, оскільки при будь-якому ${\displaystyle \varepsilon >0}$ можна вказати відрізок скільки завгодно малої довжини такий, що на його кінцях значення функції відрізнятимуться більше, ніж на ${\displaystyle \varepsilon .}$ Інший приклад: функція

${\displaystyle f(x)=x^{2},\;x\in (-\infty ,+\infty )}$

неперервна на всій числовій осі, але не є рівномірно неперервною, оскільки

${\displaystyle \lim _{x\to \infty }(f\left(x+{\frac {a}{x}}\right)-f(x))=\lim _{x\to \infty }(x^{2}+2a+a^{2}x^{-2}-x^{2})=2a.}$

Для будь-якого ${\displaystyle \varepsilon >0}$ можна вибрати відрізок як завгодно малої довжини ${\displaystyle \varepsilon /x}$ такий, що різниця значень функції ${\displaystyle f(x)=x^{2}}$ на кінцях відрізка буде більше ${\displaystyle \varepsilon .}$ Зокрема, на відрізку ${\displaystyle \left(x,x+{\frac {\varepsilon }{x}}\right)}$ різниця значень функції збігається до ${\displaystyle 2\varepsilon .}$

• (Теорема Кантора — Гейне) Функція, неперервна на компактній підмножині ${\displaystyle K\subset X,}$ рівномірно неперервна на ній. Зокрема якщо ${\displaystyle f\in C{\bigl (}[a,b]{\bigr )},}$ то вона рівномірно неперервна на ${\displaystyle [a,b].}$
• Нехай ${\displaystyle f\colon X\to Y}$ це рівномірно неперервне відображення, і ${\displaystyle \{x_{n}\}_{n=1}^{\infty }}$ — послідовність Коші в ${\displaystyle X.}$ Тоді ${\displaystyle {\bigl \{}f(x_{n}){\bigr \}}_{n=1}^{\infty }}$ — послідовність Коші в ${\displaystyle Y.}$
• Будь-яке ліпшицеве відображення є рівномірно неперервним.

Див. також

• Рівностепенева неперервність
• Абсолютна неперервність

Джерела

• Григорій Михайлович Фіхтенгольц. Курс диференціального та інтегрального числення. — 2025. — 2391 с.(укр.)
• Ляшко І.І., Ємельянов В.Ф., Боярчук О.К. Математичний аналіз. Частина 1. — К. : Вища школа, 1992. — 496 с. — ISBN 5-11-003757-4.(укр.)
• Ляшко І. І., Боярчук О. К., Гай Я. Г., Головач Г. П. Математичний аналіз в прикладах і задачах. — 2025. — 800+ с.(укр.)
• Бурбакі Н. Загальна топологія: Основні структури. — 3-е. — М. : Наука, 1968. — С. 276. — (Елементи математики)(рос.)
• Банах С. Диференціальне та інтегральне числення = Rachunek różniczkowy i całkowy. — 2-е. — М. : Наука, 1966. — 436 с.(рос.)