Шестисоткомірник

Пра́вильний шестисоткомі́рник, або просто шестисоткомі́рник^[1], або гекзакосіхор (від дав.-гр. ἑξἀκόσιοι — «шістсот» і χώρος — «місце, простір») — один із шести правильних багатокомірників у чотиривимірному просторі. Двоїстий стодвадцятикомірнику.

Шестисоткомірник
Діаграма Шлегеля: проєкція (перспектива) шестисоткомірника в тривимірний простір
Тип	правильний чотиривимірний політоп
Символ Шлефлі	{3,3,5}
Комірок	600
Граней	1200
Ребер	720
Вершин	120
Вершинна фігура	ікосаедр
Двоїстий політоп	стодвадцятикомірник

Проєкція обертового шестисоткомірника в тривимірний простір

Розгортка

Відкрив Людвіг Шлефлі в середині 1850-х років^[2]. Символ Шлефлі шестисоткомірника — {3,3,5}.

Опис

Обмежений 600 тривимірними комірками — однаковими правильними тетраедрами. Кут між двома суміжними комірками дорівнює ${\displaystyle \arccos \left(-{\frac {1+3{\sqrt {5}}}{8}}\right)\approx 164{,}48^{\circ }.}$

1200 двовимірних граней — однакові правильні трикутники. Кожна грань розділяє 2 комірки, що прилягають до неї.

Має 720 ребер рівної довжини. На кожному ребрі сходяться по 5 граней та по 5 комірок.

Має 120 вершин. У кожній вершині сходяться по 12 ребер, по 30 граней і 20 комірок.

У координатах

Шестисотячейник можна розмістити в декартовій системі координат так, щоб:

• 8 його вершин мали координати ${\displaystyle (\pm 2;0;0;0),}$${\displaystyle (0;\pm 2;0;0),}$${\displaystyle (0;0;\pm 2;0),}$${\displaystyle (0;0;0;\pm 2)}$ (ці вершини розташовані так само, як вершини шістнадцятикомірника);

• ще 16 вершин — координати ${\displaystyle (\pm 1;\pm 1;\pm 1;\pm 1)}$ (розташовані так само, як вершини тесеракта ; крім того, разом з 8 попередніми вони дають вершини двадцятичотирьохкомірника);

• координати інших 96 вершин були різними парними перестановками чисел ${\displaystyle (\pm \Phi$ ;\pm 1;\pm \Phi ^{-1};0),} де ${\displaystyle \Phi ={\frac {1+{\sqrt {5}}}{2}}}$ — відношення золотого перетину (ці вершини розташовані так само, як вершини кирпатого двадцятичотирьохкомірника).

Початок координат ${\displaystyle (0;0;0;0)}$ буде центром симетрії багатокомірника, а також центром його вписаної, описаної та напіввписаних тривимірних гіперсфер.

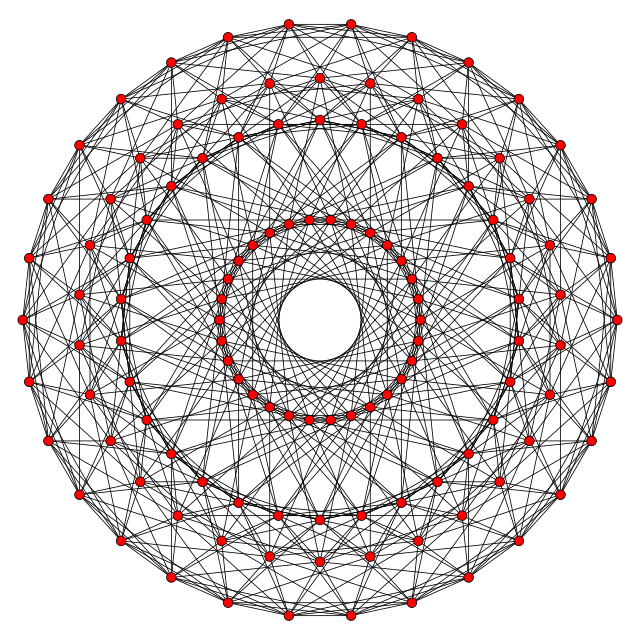
Ортогональні проєкції на площину

Метричні характеристики

Якщо шестисоткомірник має ребро довжини ${\displaystyle a,}$ то його чотиривимірний гіпероб'єм і тривимірна гіперплоща поверхні виражаються відповідно як

${\displaystyle V_{4}={\frac {25}{4}}\left(2+{\sqrt {5}}\right)a^{4}\approx 26{,}4754249a^{4},}$

${\displaystyle S_{3}=50{\sqrt {2}}a^{3}\approx 70{,}7106781a^{3}.}$

Радіус описаної тривимірної гіперсфери (що проходить через усі вершини багатокомірника) при цьому дорівнює

${\displaystyle R=\Phi a={\frac {1}{2}}\left(1+{\sqrt {5}}\right)a\approx 1{,}6180340a,}$

радіус зовнішньої напіввписаної гіперсфери (що дотикається до всіх ребер у їхніх серединах) -

${\displaystyle \rho _{1}={\frac {1}{2}}{\sqrt {5+2{\sqrt {5}}}}\;a\approx 1{,}5388418a,}$

радіус внутрішньої напіввписаної гіперсфери (що дотикається до всіх граней у їхніх центрах)

${\displaystyle \rho _{2}={\frac {1}{6}}\left({\sqrt {15}}+3{\sqrt {3}}\right)a\approx 1{,}5115226a,}$

радіус вписаної гіперсфери (що дотикається до всіх комірок у їхніх центрах) -

${\displaystyle r={\frac {1}{4}}\left({\sqrt {10}}+2{\sqrt {2}}\right)a\approx 1{,}4976762a.}$