热门问题
时间线
聊天
视角
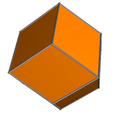
倒角立方体
来自维基百科,自由的百科全书
Remove ads
在几何学中,倒角立方体又称切棱立方体或裁边立方体(英语:Chamfered Cube)是一种凸十八面体,共有18个面、48个边和32个顶点[1],是四角化截半立方体的对偶多面体,是由立方体经过倒角变换所产生的多面体,是一种方富勒烯[3]。
Remove ads
性质
倒角立方体具有偶数边数的面且180度旋转对称的边,因此可以算作一种环带多面体,也是一个从立方体不使用膨胀变换构造的一个环带多面体之一[4],然后又因由正方形和六边形的面组成,因此也属于一种八面体对称的[5]戈德堡多面体,符号为GIV(0,2)。此外由于倒角立方体拥有接近正多边形的面,且有很多面都是正多边形(六个正方形),因此也是一种拟詹森多面体。
倒角立方体具有18个面、48个边和32个顶点,由6个正方形和12个六边形组成[2]。其结构可视为部分顶点被截去的菱形十二面体,共截去了6个顶点,原本的十二个菱形变为十二个六边形,截去的顶点变为六个正方形。
由于六边形是因为切割而产生的,因此是全等,每个边皆等边,但不是正六边形,两个内角的角度跟原来的菱形十二面体相同,为arccos(-1/3),约109.47度,而新截出来的四个内角约为125.26度,而正六边形内角是120度[6]。
另外一种构造出倒角立方体的方式是由正方体出发,将原本的面扩张,原本的角倒过来,剩下的空隙用六边形填满
此外,也可以看作是一种截边的立方体,即将立方体的十二条边切去[7],切面即变成六边形,或者是看成将边以六边形替代。
倒角立方体可以视为切去所有四阶顶点的菱形十二面体,即切去切去相邻四个面的顶点,因此也称为截四阶角菱形十二面体,有时会简称为截角菱形十二面体[8],但这种简称不合适,因为可能是指倒角八面体[9]。
另外,倒角立方体也可以视为经过交错截角的菱形十二面体,即交错地切除菱形十二面体的顶点,但不是完全切除,因为完全切除会导致原有的菱形面退化成二边形,即退化为边,造成结果变为立方体,因此,倒角立方体也可以称为交错截角菱形十二面体,同样,这称呼存在歧义,因为也可能是指倒角八面体[9],不同于交错的扭棱立方体,其结果仅是两种手性镜像,而此例中的结果是倒角八面体以及倒角立方体。
Remove ads
倒角立方体是菱形十二面体的闵可夫斯基和[10],若立方体边长为一的时候,原本菱形十二面体的八个顶点是位在,剩余六个顶点是的所有排列组合。
边长为a的倒角立方体,其体积为:
- .
表面积为:
Remove ads
倒角倒角立方体
倒角倒角立方体或二次倒角立方体,即进行两次倒角的立方体,亦可以称为倒角交错截角菱形十二面体。
下表列出立方体倒角四次以下的多面体。蓝色代表来自于正方体的面、绿色代表经过一次倒角后产生的面、红色是两次、紫色是三次、黄色是四次。前几个的面数是6, 18, 66, 258, 1026, 4098,...... (OEIS数列A178789)、边数是12, 48, 192, 768, 3072, 12288,...... (OEIS数列A164346)、顶点数是2, 8, 32, 128, 512, 2048, 8192,...... (OEIS数列A004171)。其顶点数皆为二次幂,因此对偶多面体也是2n面体。此外,这些多面体全部都是戈德堡多面体[11]。
Remove ads
相关多面体
倒角立方体有一个对称性为五角十二面体群的拓朴同构体,其可以透过截去五角十二面体中与坐标轴平行的棱构造。这种立体为黄铁矿的晶形之一。
|
五角十二面体和其截去与坐标轴平行的棱之结果 |
矿石晶形模型 |
这种立体也可以视为特殊的切棱立方体,其可以透过切角小于45度且深度大于零的方式切去立方体的棱来构造[12]。


倒角立方体与截角八面体十分类似。
倒角立方体是立方体透过一种截边的变换产生的,截边也可以产生一些不同的多面体,例如:
倒角立方体是一种正多面体倒角变换结果,其他正多面体或卡塔兰立体也可以透过倒角变换得到一系列的多面体:
倒角立方体也是一种多边形-六边形镶嵌。
参见
参考文献
外部链接
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads