乘法

乘法（英語、法語：multiplication）是四則運算之一。乘法運算的本質，就是​​「同類累加的簡寫形式​​」。

3×4 = 12

例如：

${\displaystyle a\times b=\underbrace {b+\cdots +b} _{a{\text{ 个 b}}}.}$

${\displaystyle a}$ 和 ${\displaystyle b}$ 都是本式的因數（或稱約數），其運算結果稱為積。

須注意的是，華人地區有將四則運算的被運算數和運算數統一位置，唸作「a 乘以 b」（「a times b」）或「b 乘 a」（「a multiplied by b」）。前者 ${\displaystyle a}$ 是乘數，${\displaystyle b}$ 是被乘數，後者則相反。而乘數和被乘數的交替並不會影響乘法的結果。^[1][2]

乘法運算亦有其它形象理解：對於整數乘法，可表現為將對象排列成矩形陣列；對於實數乘法，則可解釋為計算矩形面積。同樣地，運算結果不受邊長測量順序的影響。

在乘法基本概念的基礎上，序列乘積、向量乘法、複數及矩陣運算等均對其進行了概念擴展。這些更高級的數學結構會以各自方式影響乘法的基本性質——例如矩陣乘法和某些向量乘法會呈現非交換性，複數乘法則會改變複數的符號。

引言

首先，進入正題前，我們不妨來看兩個生活中的例子：

• 買5個單價為3圓的冰激凌：由${\displaystyle 5\times 3=15}$可得，需要支付15圓。
• 要搭一個3層高、每層4塊積木的小塔：由${\displaystyle 3\times 4=12}$可得，需要12塊積木。

其次，數學和物理存在許多「累加關係」：

• 已知勻速直線運動狀態下，某物體行進速度為 ${\displaystyle v}$ ，所用時間為 ${\displaystyle t}$ ，可得累計距離 ${\displaystyle d=v\times t}$ ；
• 已知一個物體的密度為 ${\displaystyle \rho }$ （假設密度均勻），體積為 ${\displaystyle V}$ ，可得其質量 ${\displaystyle m=\rho \times V}$ ；

......

可見，在數學，尤其是在基本算術中，乘法是​​加法的「快捷版」​​。

定義

基本定義

乘法運算，指通過特定法則將兩個或多個數結合生成積的運算過程。其核心內涵包括：

1. 同類累加的簡寫形式：表示將相同值的數進行連續疊加的運算（如 ${\displaystyle 3\times 4=4+4+4=12}$ ）
2. 比例關係的量化表達：當乘數非整數時，可表示為原數的分數（小數）倍（如 ${\displaystyle 3\times 0.5}$ 表示 ${\displaystyle 3}$ 的一半，${\displaystyle 4\times {\dfrac {1}{3}}}$ 表示 ${\displaystyle 4}$ 的三分之一）
3. 維度擴展的數學工具：在幾何學中，用於計算面積（長 ${\displaystyle \times }$ 寬）、體積（長 ${\displaystyle \times }$ 寬 ${\displaystyle \times }$ 高）等空間度量

符號與表示

主條目：乘號

乘法可以用幾種方法表示。以下的式子表示「五乘以二」：

• ${\displaystyle 5\times 2}$
• ${\displaystyle 5\cdot 2}$
• ${\displaystyle 5*2}$
• ${\displaystyle (5)(2)}$

古代常用的方法是將兩個數並排，沒有甚麼特別的符號來表示乘法。

以「${\displaystyle \times }$」表示乘法，是由奧特雷德於1618年最先引入，也是現在最流行的寫法。在計算機領域，也有為方便鍵盤輸入而以小寫英文字母「x」替代「×」。

以「${\displaystyle \cdot }$」表示乘法，如今已成為美國^[3][4]、德國、法國等國家^[5]的標準。其最早由托馬斯·哈里奧特於1631年出版的著作使用，但令這種用法影響深遠的人是萊布尼茲。

因為星號「${\displaystyle *}$」是鍵盤必備的符號，電腦常用其表示乘號，這種用法起源於FORTRAN語言。

代數中，為方便書寫，乘號常被略去（如 ${\displaystyle 5x}$ 和 ${\displaystyle xy}$ ）。但如果變數多於一個字母，則易令人混淆。同時如果只有數字，乘號則不應略去，如 ${\displaystyle 5\times 2}$ 不會表示成 ${\displaystyle 52}$ 。

累乘則用大寫希臘字母 ${\displaystyle \Pi }$（Pi）表示：

${\displaystyle \prod _{i=m}^{n}x_{i}:=x_{m}\cdot x_{m+1}\cdot x_{m+2}\cdot \ldots \cdot x_{n-1}\cdot x_{n}}$

性質

乘法運算的數學性質在不同定義和數系下具有多樣性，以下是主要分類及詳細說明。

基本運算律

1. 交換律：${\displaystyle xy=yx}$
2. 結合律：${\displaystyle (xy)z=x(yz)}$
3. 分配律：${\displaystyle x(y+z)=xy+xz}$

單位元、零元與逆元性質​

1. 乘法單位律：任何數乘以 ${\displaystyle 1}$ ，都會等於該數本身，即${\displaystyle 1x=x}$。此律可擴展至多項式中的常數項。
2. 零元性質：任何數乘以 ${\displaystyle 0}$ ，即是甚麼也沒做過，結果為零，即${\displaystyle 0x=0}$。同樣地，多個因數中若含 ${\displaystyle 0}$ ，積必為 ${\displaystyle 0}$ 。
3. 逆元性質：非零數 ${\displaystyle a}$ 的逆元（亦為其倒數）為 ${\displaystyle {\dfrac {1}{a}}}$ ，滿足 ${\displaystyle a\times {\dfrac {1}{a}}=1}$ 。

特殊數系下的性質​

實數與複數除法

1. 滿足交換律、結合律、分配律。
2. 複數乘法涉及模長和輻角的變化。

矩陣乘法

1. 滿足結合律和分配律，但​​不滿足交換律，特殊矩陣（如對角矩陣）除外。
2. 對零矩陣：所有元素為 ${\displaystyle 0}$ 的矩陣，與任意矩陣相乘結果為零矩陣。

模運算

在模 ${\displaystyle n}$ 下，乘法逆元存在當且僅當數與 ${\displaystyle n}$ 互質（如模質數時所有非零數均有逆元）。

不同的乘法運算

兩個數的乘法運算或積（這兩個數可以是自然數、整數、分數、實數、複數、四元數等）的數學定義，相似而又各有特性。

自然數乘法

兩個自然數 ${\displaystyle m,n\in \mathbb {N} }$ ，其乘積為：

${\displaystyle mn=nm=\sum _{k=1}^{n}m=\sum _{k=1}^{m}n}$

這是將該整數自身重複相加若干次的簡寫法。換言之：

${\displaystyle mn=nm=\underbrace {m+m+m+\cdots +m} _{n{\text{个 m}}}=\underbrace {n+n+n+\cdots +n} _{m{\text{个 n}}}}$

長遠來看，將乘法視為重複加法並不高效。因此，數學家歸納了從 ${\displaystyle 1}$ 到 ${\displaystyle 9}$ 的乘法結果，即九九乘法表。

多個自然數相乘時，我們使用括號標明運算順序。為避免過多括號，規定以下優先級規則：乘法始終優先於加法。例如在表達式 ${\displaystyle 4+5\times 2}$ 中，應理解為 ${\displaystyle 4+(5\times 2)=4+10=14}$ ，而非 ${\displaystyle (4+5)\times 2=9\times 2=18}$ 。

當${\displaystyle x}$是量，${\displaystyle y}$是自然數時，定義乘法遞歸如下：

${\displaystyle 0x=0}$

${\displaystyle xy=x+x(y-1)}$

整數乘法

圖中，笛卡兒坐標系的藍色區域表示乘積為正，紅色區域表示乘積為負。

在數軸上表示整數乘法時，可藉助向量的方向與長度直觀理解

整數乘法推廣自然數乘法至負數，符號規則為：同號得正，異號得負，絕對值相乘。

分數（小數）乘法

兩個分數 ${\displaystyle {\frac {z}{n}},{\frac {z'}{n'}}}$ 作乘法運算時，分子與分子相乘，分母與分母相乘：

${\displaystyle {\frac {z}{n}}\cdot {\frac {z'}{n'}}={\frac {z\cdot z'}{n\cdot n'}}}$

當且僅當 ${\displaystyle n,n'\neq 0}$ 時成立。

兩個小數作乘法運算時，可利用乘法交換律的特性進行計算。

例如，計算 ${\displaystyle 43.1}$ 乘以 ${\displaystyle 1.215}$ 時：

${\displaystyle {\begin{aligned}43.1\times 1.215&=\left(431\times {\frac {1}{10}}\right)\times \left(1\;215\times {\frac {1}{1\;000}}\right)\\&=(431\times 1\;215)\times \left({\frac {1}{10}}\times {\frac {1}{1\;000}}\right)\\&=(431\times 1\;215)\times {\frac {1}{10\;000}}\\&={\frac {523\;665}{10\;000}}\\&=52.3665\end{aligned}}}$

可見，兩個小數作乘法運算時，先忽略小數點，計算兩數小數點後數字的位數之和，將兩數視為整數相乘，最後在結果中從右往左數出與總位數相同的位數，並放置小數點。

又如，計算 ${\displaystyle 3.15}$ 乘以 ${\displaystyle 1.2}$ 時：

1. 先計算整數部分相乘：${\displaystyle 315\times 12=3780}$
2. 再將小數點向左移動 ${\displaystyle 3}$ 位：${\displaystyle 3780\Rightarrow 3.780}$（末尾的 ${\displaystyle 0}$ 可省略，寫作 ${\displaystyle 3.78}$）

實數乘法

實數乘法是前文乘法的推廣，性質也相同。其核心在於：每個實數都是某有理數集的上確界。特別地，每個正實數是其無限小數展開式截斷序列的上確界，例如 ${\displaystyle \pi }$ 是集合 ${\displaystyle \{3,\;3.1,\;3.14,\;3.141,\ldots \}}$ 的上確界。

實數的一個基本性質是：有理逼近與算術運算（特別是乘法）相容。這意味着，若正實數 ${\displaystyle a}$ 和 ${\displaystyle b}$ 分別表示為集合 ${\displaystyle A}$ 和 ${\displaystyle B}$ 的上確界（即 ${\displaystyle a=\sup _{x\in A}x}$ ， ${\displaystyle b=\sup _{y\in B}y}$ ），則兩數乘積 ${\displaystyle a\cdot b}$ 等於所有 ${\displaystyle x\in A}$ 與 ${\displaystyle y\in B}$ 的乘積項的上確界（即 ${\displaystyle a\cdot b=\sup _{x\in A,y\in B}x\cdot y}$ ）。具體而言，兩個正實數的乘積等於其十進制展開式逐項積序列的上確界。

對於涉及負實數的乘法運算，可通過符號法則簡化處理：正負號的變化將上確界轉化為下確界。很多人都通過柯西序列構造實數，因為這種方法無需考慮四種可能的符號組合情況，從而簡化了運算規則的推導過程。

複數乘法

複數乘法可通過分配律和虛數單位性質 ${\displaystyle i^{2}=-1}$ 進行運算。具體地，兩個複數 ${\displaystyle (a+b\,i)}$ 與 ${\displaystyle (c+d\,i)}$ 作乘法運算時，展開過程為：

${\displaystyle {\begin{aligned}(a+b\,i)\cdot (c+d\,i)&=a\cdot c+a\cdot d\,i+b\,i\cdot c+b\cdot d\cdot i^{2}\\&=(a\cdot c-b\cdot d)+(a\cdot d+b\cdot c)\,i\end{aligned}}}$

其中 ${\displaystyle i^{2}}$ 替換為 ${\displaystyle -1}$ 後，實部與虛部分別合併。

用極坐標系表示複數

從幾何視角理解，複數可表示為極坐標形式：

${\displaystyle a+b\,i=r\cdot (\cos(\varphi )+i\sin(\varphi ))=r\cdot e^{i\varphi }}$

${\displaystyle c+d\,i=s\cdot (\cos(\psi )+i\sin(\psi ))=s\cdot e^{i\psi }}$

此時，複數乘法可轉化為模長與輻角的運算：

${\displaystyle (a\cdot c-b\cdot d)+(a\cdot d+b\cdot c)i=r\cdot s\cdot e^{i(\varphi +\psi )}.}$

其幾何意義在於模長相乘（ ${\displaystyle r\cdot s}$ ）、輻角相加（ ${\displaystyle \varphi +\psi }$ ）。

四元數乘法

參見：四元數 § 加、乘和一般函數

基於集合論的乘法

非負整數的乘法可通過集合論中的基數概念或皮亞諾公理進行定義。基數理論通過集合的勢（即集合元素的數量）定義乘法，例如，兩個有限集合的笛卡兒積的勢等於各自勢的乘積。而皮亞諾公理體系則通過自然數的遞歸定義實現乘法運算：設非負整數表示為自然數，其乘法可歸納定義為：

• ​​基例​​：對任意非負整數 ${\displaystyle a}$ ，有 ${\displaystyle a\times 0=0}$ ；
• 遞推規則​​：對任意非負整數 ${\displaystyle a}$ 、${\displaystyle b}$ ，有 ${\displaystyle a\times {(b+1)}=a\times b+a}$ 。

此定義通過數學歸納法可證明滿足乘法結合律、交換律等基本性質。

對於任意整數的乘法，需在自然數乘法基礎上引入符號規則。例如，負整數乘法定義為：若 ${\displaystyle a}$ 、${\displaystyle b}$ 為自然數，則 ${\displaystyle {(-a)}\times {(-b)}=a\times b}$ ，而 ${\displaystyle {(-a)}\times b=-{(a\times b)}}$ 。這一擴展保持了乘法運算的代數結構一致性。

有理數乘法則通過分數形式定義：若 ${\displaystyle {\dfrac {a}{b}}}$ 與 ${\displaystyle {\dfrac {c}{d}}}$ 為最簡分數（ ${\displaystyle b}$ 、${\displaystyle d\neq 0}$ ），則其乘積為 ${\displaystyle {\dfrac {ac}{bd}}}$ ，分母通過集合論中的笛卡爾積構造，分子通過自然數乘法定義。此過程需驗證運算的封閉性與唯一性，例如通過交叉相乘消去公約數，確保結果仍為最簡分數。

實數乘法的定義依賴於有理數乘法的完備性。通過戴德金分割或柯西序列構造實數時，乘法運算被定義為極限運算：若 ${\displaystyle \{a_{n}\}}$ 和 ${\displaystyle \{b_{n}\}}$ 為收斂的有理數序列，則實數乘積定義為 ${\displaystyle \lim(a_{n}\times b_{n})}$ 。此定義需滿足乘法與極限運算的交換性，並通過 ${\displaystyle \epsilon -\delta }$ 語言嚴格證明其合理性。

基於群論的乘法

在群論中，若一個集合在乘法運算下滿足封閉性、結合律、存在單位元且每個元素均有逆元素，則稱其構成群結構。這些公理構成了群的定義基礎。

以非零有理數集為例，其乘法運算滿足群的所有條件：單位元為1（不同於加法群的單位元0），每個非零有理數均存在乘法逆元，且乘法運算封閉（因為兩個非零有理數相乘仍為非零有理數）。但需注意的是，零必須被排除，因其乘法逆元不存在。此例中的群為阿貝爾群，但群論中並非所有乘法群均為阿貝爾群。

考慮可逆方陣群：給定域上同維數的可逆矩陣集合，其乘法運算滿足封閉性（矩陣相乘仍為同維可逆矩陣）、結合律、單位矩陣作為單位元，且每個矩陣均有逆矩陣。然而，矩陣乘法不滿足交換律（如 ${\displaystyle {AB}\neq {BA}}$ ），因此該群為非阿貝爾群。

即使排除零元素，整數集在乘法下也不構成群。原因在於除 ${\displaystyle 1}$ 和 ${\displaystyle -1}$ 外，其他整數均無乘法逆元。這一特性凸顯了乘法群對逆元存在與否的嚴格要求。

群的乘號通常表示為點乘（${\displaystyle \cdot }$）或直接省略不寫。在描述群時，點乘符號常用於明確運算，例如非零有理數乘法群可記為（ ${\displaystyle \mathbb {Q} \{0\},\cdot }$ ）。這種符號體系與加法群（如（ ${\displaystyle \mathbb {Z} ,+}$ ））形成對比，體現了運算類型的差異。

運算方法

歷史上的算法

迄今為止發現的最早的乘法運算，是可追溯至舊石器時代初期的伊尚戈骨上的刻痕。劃痕可能是計數符號，也可能只是為了方便抓握，或有其他非數學的目的。^[6]

古埃及人採用連續加倍法進行整數和分數的乘法運算，這一方法在《萊因德數學紙草書》中有詳細記載。^[7]例如，計算 ${\displaystyle 13\times 21}$ 時，通過將${\displaystyle 21}$依次加倍三次得到${\displaystyle 42}$、${\displaystyle 84}$、${\displaystyle 168}$，再根據加倍序列中的對應項，得出 ${\displaystyle {(1+4+8)}\times 21=273}$ 。

巴比倫人使用六十進制系統，其乘法運算與現代十進制類似，但因 ${\displaystyle 60\times 60=3600}$ 種組合過多，他們通過製作包含前${\displaystyle 20}$個基數倍數的乘法表（如 ${\displaystyle n,2n,\ldots ,20n}$ 及 ${\displaystyle 30n,40n,50n}$ ）來簡化計算，如 ${\displaystyle 53n}$ 可通過 ${\displaystyle 50n+3n}$ 的組合快速得出。

古希臘人以幾何圖形（如矩形）表示乘法，體現「乘積即面積」的思想。歐幾里得更是在《幾何原本》中用幾何方法證明乘法分配律。

孫子籌算乘法

中國古代擁有史上最早、最詳細的​​十進制位值制​​乘法規則，其首見於南北朝時期的孫子算經。孫子乘法的核心，是通過縱橫排列的算籌模擬位值運算，如計算 ${\displaystyle 49\times 36}$ 時，先以算籌擺出 ${\displaystyle 49}$ 和 ${\displaystyle 36}$ ，再按「九九表」逐位相乘並累加，終得 ${\displaystyle 1764}$ 。這種算法在9世紀傳至中東，13世紀又譯成拉丁文而流行於歐洲。至於九九乘法表​​，則在戰國時期已成熟應用^[8]，其採用「小九九」形式，從「九九八十一」到「一一如一」，比古埃及的累加法效率提升數十倍。

阿拉伯穆斯林於9世紀引入印度數字和位值制，結合阿拉伯語符號形成計算體系，推動乘法運算標準化。而數學家花拉子米在接納中國的孫子乘法後，在《代數學》中將乘法與方程系統化結合，提出「還原與對消」法，將乘法納入代數運算框架，影響歐洲數學發展。

印度類似「鋪地錦」的圖形化乘法

納皮爾的骨頭

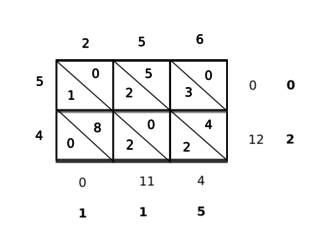
印度古代的乘法運算亦有發展。7世紀，數學家婆羅摩笈多提出「交叉相乘法」，即 ${\displaystyle (a+b)(c+d)=ac+ad+bc+bd}$ ，簡化多位數乘法步驟。例如計算 ${\displaystyle {123}\times {456}}$ 時，通過分項相乘再求和，減少重複計算。12世紀，印度文獻中出現類似中國古代「鋪地錦」的圖形化乘法，通過網格線段交叉點計數得出結果，後經阿拉伯傳入歐洲。「納皮爾的骨頭」便是借鑑「鋪地錦」的靈感產生的。

現代算法

現代基於印度-阿拉伯數字系統的乘法，最早同樣由婆羅摩笈多系統闡述。他在7世紀著作《婆羅摩修正體系》中完整定義了加、減、乘、除四則運算的規則，其乘法體系包含多種算法，現代豎式乘法即源於此。此算法通過花拉子米的著作《印度數字算術》於9世紀初傳入阿拉伯世界，其《代數學》系統整合了印度數字與運算規則。13世紀，意大利數學家斐波那契在《計算之書》中推廣此法，最終使印度-阿拉伯數字系統取代羅馬數字成為歐洲主流。^[9]

由於歷史影響，華人小學生現在仍背誦九九乘法表來學習乘法。

關於電腦的特別算法，以及其它現代運算法，詳見乘法算法。

其它算法

用手指算乘法

除了加法，在有限範圍內，乘法也可以用手指完成。為此，兩個因數需處於同一十位半區，也就是說，兩者要麼均以 ${\displaystyle 1}$ 至 ${\displaystyle 5}$ 結尾，要麼均以 ${\displaystyle 6}$ 至 ${\displaystyle 0}$ 結尾。

對於因數以 ${\displaystyle 1}$ 至 ${\displaystyle 5}$ 結尾的情況：

1. 首先為手指編號：從小指開始，依次標記為 ${\displaystyle 10\cdot {(d-1)}+1}$ 至拇指為 ${\displaystyle 10\cdot {(d-1)}+5}$ （其中 ${\displaystyle d}$ 表示對應數的十位，如第二位為 ${\displaystyle 1}$ 時，對應 ${\displaystyle 11}$ 至 ${\displaystyle 15}$ ）；
2. 對齊兩個因數的手指後，數出下方手指總數（包括對齊的手指），將其乘以 ${\displaystyle d\cdot 10}$ ；
3. 計算左右手下方手指（不包含對齊的手指）的乘積；
4. 最後，加上常數項 ${\displaystyle {d^{2}}\cdot 100}$ ，結果即為所求。

對於因數以 ${\displaystyle 6}$ 至 ${\displaystyle 0}$ 結尾的情況：

1. 類似地，從小指開始，依次標記為 ${\displaystyle 10\cdot {(d-1)}+6}$ 至拇指為 ${\displaystyle 10\cdot d}$ （其中 ${\displaystyle d}$ 表示對應數的十位，如第二位為 ${\displaystyle 1}$ 時，對應 ${\displaystyle 16}$ 至 ${\displaystyle 20}$ ）；
2. 對齊兩個因數的手指後，數出下方手指總數（包括對齊的手指），將其乘以 ${\displaystyle d\cdot 10}$ （同上）；
3. 計算左右手上方手指（不包含對齊的手指）的乘積（同上）；
4. 最後，加上常數項 ${\displaystyle d\cdot {(d-1)}\cdot 100}$ ，結果即為所求。

以 ${\displaystyle 7\times 8}$ 為例： ${\displaystyle 7}$ 和 ${\displaystyle 8}$ 均以 ${\displaystyle 6}$ 至 ${\displaystyle 0}$ 結尾，而 ${\displaystyle d=1}$ 。對齊手指後，下方手指有 ${\displaystyle 5}$ 根，乘以 ${\displaystyle 1\times 10=10}$ 得 ${\displaystyle 50}$ ；上方手指分別為 ${\displaystyle 3}$ 根和 ${\displaystyle 2}$ 根，積為 ${\displaystyle 3\times 2=6}$ ；加法常數項 ${\displaystyle {(1-1)}\cdot 1\cdot 100=0}$，總和為 ${\displaystyle 50+6+0=56}$ 。

再如 ${\displaystyle 24\times 22}$ ： ${\displaystyle 24}$ 和 ${\displaystyle 22}$ 均以 ${\displaystyle 1}$ 至 ${\displaystyle 5}$ 結尾，而 ${\displaystyle d=2}$ 。對齊手指後，下方手指有 ${\displaystyle 6}$ 根，乘以 ${\displaystyle 2\times 10=20}$ 得到 ${\displaystyle 120}$ ；下方手指分別為 ${\displaystyle 4}$ 根和 ${\displaystyle 2}$ 根，積為 ${\displaystyle 4\times 2=8}$ ；加法常數項 ${\displaystyle {2^{2}}\cdot 100=400}$ ，總和為 ${\displaystyle 120+8+400=528}$ 。

此方法尤其適用於快速心算平方數。對於不同十位或十位半區的因數，可通過分解為和的形式（如 ${\displaystyle {(a+x)}\cdot {(a+y)}}$ ）應用該技巧。其數學原理基於多項式展開：

${\displaystyle (a+x)\cdot (a+y)=a^{2}+(x+y)\cdot a+x\cdot y}$

尺規作圖法

從相交弦定理出發的尺規法

圖1
利用相交弦定理算乘法

如圖1所示，過點 ${\displaystyle O}$ 作一直線，分別在 ${\displaystyle O}$ 點兩側截取長度為 ${\displaystyle a}$ 和 ${\displaystyle b}$ 的線段，得點 ${\displaystyle A}$ 和 ${\displaystyle B}$ 。再從 ${\displaystyle O}$ 出發，沿另一方向作射線，截取單位長度 ${\displaystyle 1}$ ，得點 ${\displaystyle E}$ 。過 ${\displaystyle A}$ 、${\displaystyle B}$ 、${\displaystyle E}$ 三點作外接圓，該圓與第二條射線的交點 ${\displaystyle C}$ 滿足相交弦定理：

${\displaystyle a\cdot b={\overline {OA}}\cdot {\overline {OB}}=\underbrace {\overline {OE}} _{=1}\cdot \,{\overline {OC}}}$

${\displaystyle {\overline {OE}}=1\Longrightarrow {\overline {OC}}=a\cdot b}$

此法通過構造三角形外接圓，將乘法轉化為幾何長度的投影關係。

從割線定理出發的尺規法

圖2
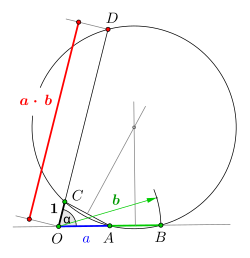
利用割線定理算乘法

如圖2所示，設圓外一點 ${\displaystyle O}$ ，沿同一方向截取長度為 ${\displaystyle a}$ 和 ${\displaystyle b}$ 的線段，得點 ${\displaystyle A}$ 和 ${\displaystyle B}$ 。過 ${\displaystyle O}$ 作與 ${\displaystyle BO}$ 成任意角 ${\displaystyle \alpha }$ 的射線，在該射線上截取單位長度 ${\displaystyle 1}$ ，得點 ${\displaystyle C}$ 。作 ${\displaystyle AB}$ 和 ${\displaystyle AC}$ 的垂直平分線以確定圓心，過 ${\displaystyle A}$ 、 ${\displaystyle B}$ 、 ${\displaystyle C}$ 三點作外接圓，該圓與射線交於點 ${\displaystyle D}$ 。根據割線定理：

${\displaystyle a\cdot b={\overline {OA}}\cdot {\overline {OB}}={\overline {OC}}\cdot \,{\overline {OD}}}$

通過調整射線角度 ${\displaystyle \alpha }$ ，可利用相似三角形關係將乘積轉化為圓外一點到交點的距離。

從相似三角形出發的尺規法

圖3
利用相似三角形算乘法

如圖3所示，在射線 ${\displaystyle A}$ 上截取單位長度 ${\displaystyle 1}$ 和長度 ${\displaystyle b}$ ，得點 ${\displaystyle E}$ 和 ${\displaystyle B}$ ，從 ${\displaystyle E}$ 出發，沿另一方向截取長度 ${\displaystyle a}$ ，得點 ${\displaystyle C}$ 。過 ${\displaystyle C}$ 作與 ${\displaystyle AB}$ 平行的直線，與過 ${\displaystyle A}$ 的射線交於點 ${\displaystyle D}$ 。由相似三角形關係可得：

${\displaystyle {\dfrac {\overline {AB}}{\overline {AC}}}={\dfrac {\overline {BD}}{\overline {BC}}}\Longrightarrow {\overline {BD}}=a\cdot b}$

此法通過構造平行線與相似三角形，將乘法運算轉化為幾何比例問題。