热门问题
时间线
聊天
视角
双曲函数
與三角函數類似的函數 来自维基百科,自由的百科全书
Remove ads
在数学中,双曲函数是一类与常见的三角函数(也叫圆函数)类似的函数。最基本的双曲函数是雙曲正弦函数和雙曲餘弦函数,从它们可以导出双曲正切函数等,其推导也类似于三角函数的推导。双曲函数的反函数称为反双曲函数。
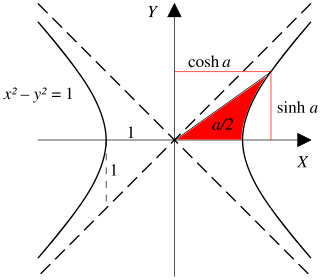
双曲函数的定义域是实数,其自变量的值叫做双曲角。双曲函数出现于某些重要的线性微分方程的解中,譬如說定义悬链线和拉普拉斯方程。
Remove ads
基本定义
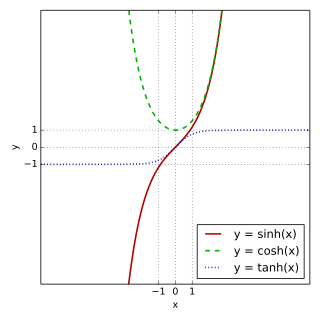

最簡單的幾種雙曲函數為[1]:
如同当遍历实数集时,点(, )的轨迹是一个圆一样,当遍历实数集时,点(, )的轨迹是單位雙曲線的右半边。这是因为有以下的恒等式:
Remove ads
歷史

在18世紀,約翰·海因里希·蘭伯特引入雙曲函數[2],並計算了雙曲幾何中雙曲三角形的面積[3]。自然對數函數是在直角雙曲線下定義的,可構造雙曲線直角三角形,底邊在線上,一個頂點是原點,另一個頂點在雙曲線。這裡以自然對數即雙曲角作為參數的函數,是自然對數的逆函數指數函數,即要形成指定雙曲角,在漸近線即x或y軸上需要有的或的值。顯見這裡的底邊是,垂線是。
單位雙曲線中雙曲線扇形的面積是對應直角雙曲線下雙曲角的。
Remove ads
虛數圓角定義
所以雙曲函數和可以通過圓函數來定義。這些恆等式不是從圓或旋轉得來的,它們應當以無窮級數的方式來理解。特別是,可以將指數函數表達為由偶次項和奇次項組成,前者形成函數,後者形成了函數。函數的無窮級數可從得出,通過把它變為交錯級數,而函數可來自將變為交錯級數。上面的恆等式使用虛數,從三角函數的級數的項中去掉交錯因子,來恢復為指數函數的那兩部份級數。
雙曲函數可以通過虛數圓角定義為:
Remove ads
與三角函數的類比
奧古斯都·德·摩根在其1849年出版的教科書《Trigonometry and Double Algebra》中將圓三角學擴展到了雙曲線[4]。威廉·金頓·克利福德在1878年使用雙曲角來參數化單位雙曲線。

|

|
給定相同的角α,在雙曲線上計算雙曲角的量值(雙曲扇形面積除以半徑)得到雙曲函數,角得到三角函數。在單位圓和單位雙曲線上,双曲函数与三角函数有如下的关係:
Remove ads
恆等式
与双曲函数有关的恆等式如下:
- 加法公式:
- 二倍角公式:
- 和差化積:
- 半角公式:
- 其中 sgn 為符號函數。
- 若 x ≠ 0,則:
由于雙曲函數和三角函数之间的对应关系,雙曲函數的恆等式和三角函數的恒等式之间也是一一对应的。对于一个已知的三角函数公式,只需要將其中的三角函數轉成相應的雙曲函數,并将含有有兩個的積的项(包括)轉換正負號,就可得到相應的雙曲函數恆等式[5]。如
- 三倍角公式:
- 三角函数的三倍角公式为:
- 而对应的双曲函数三倍角公式则是:
- 差角公式:
Remove ads
双曲函数的導數
Remove ads
双曲函数的泰勒展開式
雙曲函數也可以以泰勒級數展開:
- (罗朗级数)
- (罗朗级数)
其中
Remove ads
無限積與連續分數形式
下列的擴展在整個複數平面上成立:
Remove ads
双曲函数的积分
Remove ads
與指數函數的關係
從雙曲正弦和餘弦的定義,可以得出如下恆等式:
和
Remove ads
複數的雙曲函數
因為指數函數可以定義為任何複數參數,也可以擴展雙曲函數的定義為複數參數。函數和是全純函數。
指數函數與三角函數的關係由歐拉公式給出:
所以:
因此,雙曲函數是關於虛部有週期的,週期為(對雙曲正切和餘切是)。
Remove ads
反双曲函数
反双曲函数是双曲函数的反函数。它们的定义为:
参考文献
参见
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads






































































































