指數分布

在機率論和統計學中，指數分布（英語：Exponential distribution）是一種連續機率分布。指數分布可以用來建模平均發生率恆定、連續、獨立的事件發生的間隔，比如旅客進入機場的時間間隔、電話打進客服中心的時間間隔、中文維基百科新條目出現的時間間隔、機器的壽命等。

指數分配

機率密度函數
累積分布函數
母數	${\displaystyle \lambda >0\,}$ 率
值域	${\displaystyle x\in [0;\infty )\!}$
機率密度函數	${\displaystyle \,\lambda e^{-\lambda x}}$
累積分布函數	${\displaystyle 1-e^{-\lambda x}}$
期望值	${\displaystyle \lambda ^{-1}\,}$
中位數	${\displaystyle \ln(2)/\lambda \,}$
眾數	${\displaystyle 0\,}$
變異數	${\displaystyle \lambda ^{-2}\,}$
偏度	${\displaystyle 2\,}$
峰度	${\displaystyle 6\,}$
熵	${\displaystyle 1-\ln(\lambda )\,}$
動差母函數	${\displaystyle \left(1-{\frac {t}{\lambda }}\right)^{-1}\,}$
特徵函數	${\displaystyle \left(1-{\frac {it}{\lambda }}\right)^{-1}\,}$

記號

指數分布即形狀母數α為1的伽瑪分布。

若隨機變數${\displaystyle X}$服從母數為${\displaystyle \lambda }$或${\displaystyle \beta }$的指數分布，則記作

${\displaystyle X\sim {\text{Exp}}(\lambda )}$ 或 ${\displaystyle X\sim {\text{Exp}}(\beta )}$

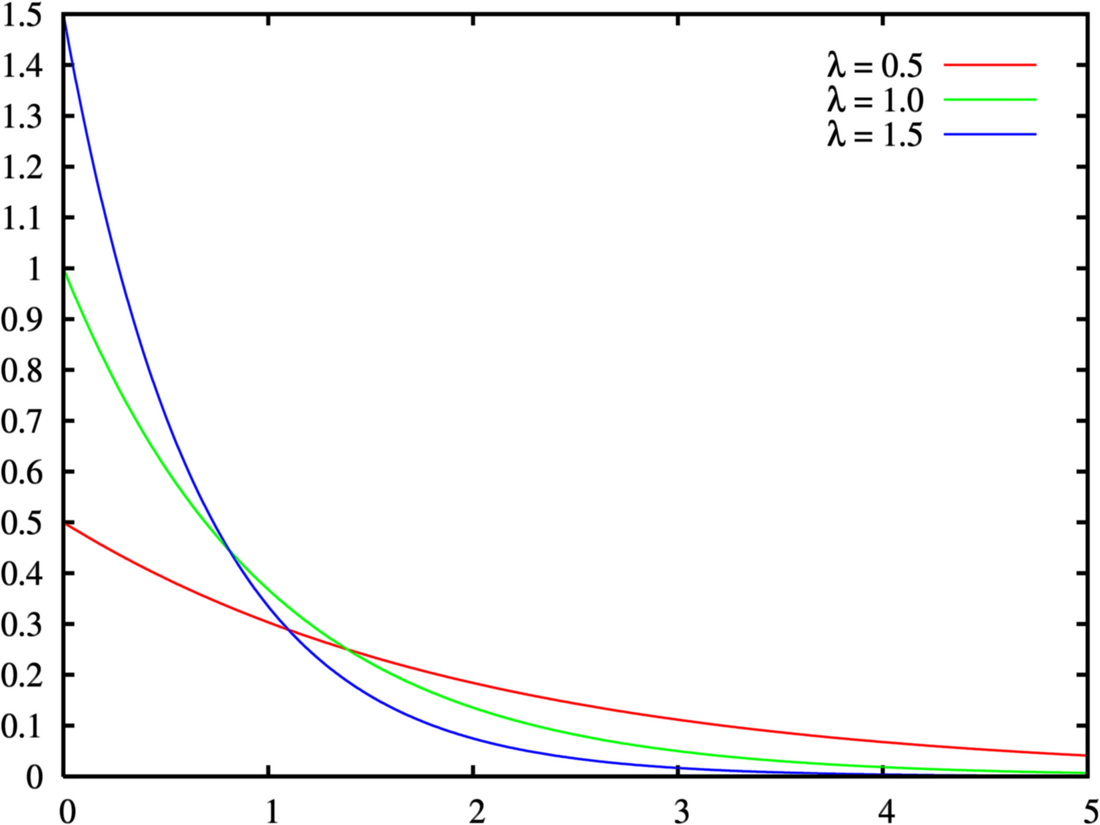
兩者意義相同，只是${\displaystyle \lambda }$與${\displaystyle \beta }$互為倒數關係。只要將以下式子做${\displaystyle {\color {Red}\lambda ={\frac {1}{\beta }}}}$的替換即可，即，指數分布之機率密度函數為：

${\displaystyle f(x;{\color {Red}\lambda })=\left\{{\begin{matrix}{\color {Red}\lambda }e^{-{\color {Red}\lambda }x}&x\geq 0,\\0&,\;x<0.\end{matrix}}\right.}$

或

${\displaystyle f(x;{\color {Red}\beta })=\left\{{\begin{matrix}{\color {Red}{\frac {1}{\beta }}}e^{-{\color {Red}{\frac {1}{\beta }}}x}&x\geq 0,\\0&,\;x<0.\end{matrix}}\right.}$

累積分布函數為：

${\displaystyle F(x;{\color {Red}\lambda })=\left\{{\begin{matrix}1-e^{-\color {Red}{\lambda }x}&,\;x\geq 0,\\0&,\;x<0.\end{matrix}}\right.}$

或

${\displaystyle F(x;{\color {Red}\beta })=\left\{{\begin{matrix}1-e^{-{\color {Red}{\frac {1}{\beta }}}x}&,\;x\geq 0,\\0&,\;x<0.\end{matrix}}\right.}$

其中${\displaystyle \lambda >0}$是分布的母數，即每單位時間發生該事件的次數；${\displaystyle \beta }$為比例母數，即該事件在每單位時間內的發生率。兩者常被稱為率母數（rate parameter）。指數分布的區間是[0,∞)。

特性

期望值與變異數

隨機變數X (X 的母數為λ或β) 的期望值是：

${\displaystyle \mathbf {E} (X)={\frac {1}{\color {Red}{\lambda }}}={\color {Red}\beta }}$

例如：如果你平均每個小時接到2次電話，那麼你預期等待每一次電話的時間是半個小時。

X 的變異數是：

${\displaystyle \mathbf {Var} (X)={\frac {1}{\color {Red}{\lambda ^{2}}}}={\color {Red}\beta ^{2}}}$

X 的偏態係數是： V[X] = 1

無記憶性

指數函數的一個重要特徵是無記憶性（Memoryless Property，又稱遺失記憶性）。這表示如果一個隨機變數呈指數分布，它的條件機率遵循：

${\displaystyle P(T>s+t\;|\;T>t)=P(T>s)\;\;{\hbox{for all}}\ s,t\geq 0.}$

與卜瓦松過程的關係

卜瓦松過程是一種重要的隨機過程。卜瓦松過程中，第k次隨機事件與第k+1次隨機事件出現的時間間隔服從指數分布。而根據卜瓦松過程的定義，長度為t的時間段內沒有隨機事件出現的機率等於

${\displaystyle {\frac {e^{-\lambda t}(\lambda t)^{0}}{0!}}=e^{-\lambda t}}$,

長度為t的時間段內隨機事件發生一次的機率等於 ${\displaystyle {\frac {e^{-\lambda t}(\lambda t)^{1}}{1!}}=e^{-\lambda t}\lambda t}$, 所以第k次隨機事件之後長度為t的時間段內，第k+n次 (n=1, 2, 3,...)隨機事件出現的機率等於${\displaystyle 1-e^{-\lambda t}}$。這是指數分布。這還表明了卜瓦松過程的無記憶性。

四分位數

率母數λ的四分位數函數（Quartile function）是：

${\displaystyle F^{-1}(p;\lambda )={\frac {-\ln(1-p)}{\lambda }},\qquad 0\leq p<1}$

• 第一四分位數：${\displaystyle \ln(4/3)/\lambda \,}$
• 中位數：${\displaystyle \ln(2)/\lambda \,}$
• 第三四分位數：${\displaystyle \ln(4)/\lambda \,}$

因此，四分位距為ln(3)/λ。

母數估計

最大概似法

給定獨立同分布樣本x = (x₁, ..., x_n)，λ的概似函數（Likelihood function）是：

${\displaystyle L(\lambda )=\prod _{i=1}^{n}\lambda \,\exp(-\lambda x_{i})=\lambda ^{n}\,\exp \!\left(\!-\lambda \sum _{i=1}^{n}x_{i}\right)=\lambda ^{n}\exp \left(-\lambda n{\overline {x}}\right)}$

其中：

${\displaystyle {\overline {x}}={1 \over n}\sum _{i=1}^{n}x_{i}}$是樣本期望值値。

概似函數對數的導數是：

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} \lambda }}\ln L(\lambda )={\frac {\mathrm {d} }{\mathrm {d} \lambda }}\left(n\ln(\lambda )-\lambda n{\overline {x}}\right)={n \over \lambda }-n{\overline {x}}\ \left\{{\begin{matrix}>0&{\mbox{if}}\ 0<\lambda <1/{\overline {x}},\\\\=0&{\mbox{if}}\ \lambda =1/{\overline {x}},\\\\<0&{\mbox{if}}\ \lambda >1/{\overline {x}}.\end{matrix}}\right.}$

母數λ的最大概似估計（Maximum likelihood）值是：

${\displaystyle {\widehat {\lambda }}={\frac {1}{\overline {x}}}}$

參見

• 拉普拉斯分布（又稱：雙指數分布）
• 幾何分布

參考文獻

1. Donald E. Knuth (1998). The Art of Computer Programming, volume 2: Seminumerical Algorithms, 3rd edn. Boston: Addison-Wesley. ISBN 0-201-89684-2. pp. 133
2. Luc Devroye (1986). Non-Uniform Random Variate Generation. New York: Springer-Verlag. ISBN 0-387-96305-7. pp. 392–401

外部連結

• 指數分布 （頁面存檔備份，存於網際網路檔案館）