热门问题
时间线
聊天
视角
斯里尼瓦瑟·拉馬努金
印度数学家（1887－1920） 来自维基百科，自由的百科全书
Remove ads
斯里尼瓦瑟·拉馬努金·艾揚加爾（英語: Srinivasa Ramanujan Aiyangar，坦米爾語：ஸ்ரீனிவாஸ ராமானுஜன் ஐயங்கார்，ISO 15919轉寫：Srīṉivāsa Rāmāṉujan Aiyaṅkār，又譯拉馬努詹、羅摩奴詹、拉曼努真，1887年12月22日—1920年4月26日），英國皇家學會院士，印度數學家，對數學分析、數論、無窮級數和連分數的研究做出了巨大貢獻。
朝露一生中，拉馬努金獨立整理出了近3900項研究成果（大部分是恆等式和方程）。[1] 其中一些原創且非常規的成果，例如拉馬努金素數、拉馬努金θ函數和模擬θ函數，開闢了全新的研究領域，並激發進一步的研究。[2]
在不同領域中，拉馬努金尤擅數論（其中多牽涉π、e等數學常數以及質數的求和公式）以及整數分拆。他慣以直覺（或稱為「數感」）導出公式，不喜證明，而後大部分公式都被證訖為實。他留存的筆記本中，那些尚未被證明的公式，啟發了幾位菲爾茲獎獲得者的工作。1997年，《拉馬努金期刊》創刊，用以發表有關「受到拉馬努金影響的數學領域」的研究論文。
Remove ads
生平
斯里尼瓦瑟出生於印度婆羅門貧窮家庭。其名字拉馬努金（Rāmāṉujan）的字面意義為「羅摩之弟」。[3] 父親庫普斯瓦米·斯里尼瓦瑟·艾揚格（Kuppuswamy Srinivasa Iyengar），原籍坦賈武爾縣，是一家紗麗店店員。母親科瑪拉塔瑪爾（Komalatammal）是一名家庭主婦，也在當地一家寺廟唱歌謀生。
1889年12月，斯里尼瓦瑟感染天花，幸而康復。後來，他隨母親搬到了馬德拉斯附近甘吉布勒姆的外婆家。1892年10月1日，斯里尼瓦瑟在當地的學校入學。[4]在外祖父丟掉法院官員的差事後，[5]他隨母親搬回了貢伯戈訥姆。[6] 祖父逝世後，斯里尼瓦瑟又被送回甘吉布勒姆而他不喜歡那裡的學校。過了半年，他又返歸貢伯戈訥姆。[6]
斯里尼瓦瑟的父親一天大部分時間都在工作，他由母親撫養長大，兩母子因此關係很好。從母親那裡，拉馬努金參習印度教傳統，閱覽往世書，學唱印度教歌曲，參加禮拜，以及保持特定的飲食習慣——以上這些皆是婆羅門文化的一部分。[7]
1897年11月，斯里尼瓦瑟以全城最高分通過了英語、淡米爾語、地理學和算術的考試，同年順利進入當地的堂高級中學就讀。在那裡，他似乎初次接受正規的數學教育。[8]
斯里尼瓦瑟自小便被視作「神童」。11歲時，他已掌握寄居家中的大學生房客的數學知識。到13歲，他從借來書籍中明瞭高等三角學的知識，同時自己發現了一些複雜的定理。[9][10]至於他的天賦，則在14歲時開始顯露。他不僅在學生時期不斷獲得榮譽證書和獎學金，還幫學校處理諸如將1,200個學生（各有不同需要）分配給35個教師的後勤事務。[11] 他甚至可以提早一半時間完成測驗，還對幾何和無窮級數方面瞭如指掌。1902年，斯里尼瓦瑟學會如何解三次方程。後來，他發展出新的四次方程解法。1903年，他嘗試研究如何解五次方程，那時他還不知道，五次方程，乃至更高次的多項式方程沒有一般的求根公式。[12]
1903年，斯里尼瓦瑟從朋友那裡得到了一本G.S.卡爾的《純粹數學概要》，詳細研究書中的內容。[13][14][15]次年，他獨立發展並研究伯努利數，還將歐拉-馬斯刻若尼常數計算至小數點後15位。[16]因此，同校的人回憶道：「我們，包括老師，很少可以理解他，並對他『敬而遠之』」。[11]
1904年，斯里尼瓦瑟被授予K. Ranganatha Rao數學獎，並榮獲獎學金，得以前往政府藝術學院就讀。[17]然而，由於太專注於研究數學，斯里尼瓦瑟在此學院之時，對於其他科目力不從心，考試大部分不及格，也因此失去獎學金。[18] 1905年8 月，斯里尼瓦瑟離家奔赴維沙卡帕特南，在拉賈蒙德里待了約莫一個月。[19]後來，他就讀於馬德拉斯的帕猜亞帕學院。在校期間，他只選擇回答自己感興趣的數學問題，其餘則不予以作答。至於英語、生理學和梵語等其他科目，他的成績並不理想。[20]
1906年，斯里尼瓦瑟投報皇家藝術學會，兩度未果，遂離開帕猜亞帕學院，獨立進行數學研究。在這個時期，他的生活相當窮困，經常吃上頓沒下頓。[21]
Remove ads
1909年7月14日，拉馬努金與賈納姬（S. Janaki Ammal；1899年3月21日-1994年4月13日）成婚。[22] 賈納姬是拉馬努金母親一年前為他遴選的，結婚時方才十歲（屆時印度境內，童婚並不鮮見）。[23][24][25] 但按照當地習俗，賈納姬繼續在娘家住了3年後，才到馬德拉斯和拉馬努金同居。[26]
婚後，拉馬努金罹患睪丸鞘膜積液。[27] 此疾病可通過常規手術治療，但家庭無力承擔費用，直至1910年1月，一位醫生自願免費為拉馬努金做了手術。[28]手術成功後，憑藉著他的數學計算能力，拉馬努金開始挨家挨戶尋求合適的文職。為賺取日常花銷，他在總統學院輔導正備考文科考試的學生。[29] 1910年末，拉馬努金再度患病，他告知好友R.艾耶爾「將他的筆記本交給帕差亞帕學院的數學教授辛加拉韋魯·穆達利亞爾，或者交給馬德拉斯基督教學院的英國教授E.B.羅斯」。[30] 康復之後，拉馬努金從艾耶爾處取回筆記本，隨後乘火車前往法國控制下的城市維盧布勒姆。[31][32] 1912年，拉馬努金曾與母親、妻子短居於馬德拉斯的佐治城。[33] 1913年5月，拉馬努金一家又遷至特里普利凱恩。[34]
1910年，與印度數學學會創始人V.艾耶爾會面後，23歲的拉馬努金被聘為馬德拉斯大學的研究員，開始在馬德拉斯的數學界嶄露頭角。[35] 拉馬努金希望能在艾耶爾所在的稅務部門找到一份工作，於是展示了自己的數學筆記。艾耶爾後來回憶道：
我震驚於其中所蘊的數學成果......我不願讓他在稅務局的最底層任職，不然只會讓他泯然眾人。[36]
幾經輾轉，艾耶爾將拉馬努金介紹給當時的印度數學學會秘書R.拉奧。[37][38][39] 拉奧對拉馬努金的成果印象深刻，只是對他的學術誠信表示質疑。經過拉馬努金朋友的努力，拉奧聆聽了拉馬努金關於橢圓積分、超幾何函數和發散級數理論的議論，並深深折服於他的才華。.[40] 有艾耶爾和拉奧多方面的支持，拉馬努金得以繼續他的數學研究。
隨後，拉馬努金的成果發表在了《印度數學學會雜誌》上。[41] 他在其中提出的首個問題，是求以下連根式的值：
在等待六個多月才找到解決方案，且一無所獲後，拉馬努金提供了一個不完整的計算方法。[42]在拉馬努金第一本筆記的第105頁，他構建了一個可用於解決連根式問題的方程：
利用這個方程，設x = 2，n = 1，a = 0，可得連根式的值是3。[43]
拉馬努金也是在此期刊上發表其首篇正式論文，他發現，一系列伯努利數的分母總是能被6整除。此外，他還設計了一種基於先前伯努利數來計算Bn的方法。其中一種如下：
可以觀察到，若n為偶數且不等於零，則：
- Bn是一個分數；
- Bn/n化為最簡形式後，其分子是一個素數；
- Bn的分母包含因數 2 和 3 各一次且僅一次；
- 2n(2n − 1)Bn/n是一個整數，因此2(2n − 1)Bn必然是一個奇數。
在1911年發表的論文《伯努利數的一些性質》中，拉馬努金給出了三個證明、兩個推論和三個猜想。[44]
拉馬努金一直渴望可以沉浸於數學海洋，而毋需做工幫補生計。他曾擔任馬德拉斯總會計師事務所的職員，但只幹了幾個星期。[45] 獲得馬德拉斯港務局的文員職位後，他在辦公室輕鬆完成分配的工作，並將閒暇時間投身於數學研究中。他的做法受到上司和同事的一致認可。[46]
Remove ads
1913年，艾耶爾、拉奧等人試圖向英國的數學家們介紹拉馬努金的工作成果。
倫敦大學學院的M.J.M.希爾並無採納，他稱拉馬努金的論文漏洞百出，「對數學有興趣，也有一定的能力」，但缺乏數學家所應有的教育基礎。[47][48] 隨後，在朋友幫助下，拉馬努金起草了給劍橋頂尖數學家的信件。[49]他發了一長串複雜的定理給三個劍橋的學術人士貝克、霍布森、哈代，只有三一學院的院士哈代注意到拉馬努金在定理中所展現的天賦。[50] 哈代和拉馬努金早在1910年時就相識，但起初他並不相信這是拉馬努金的來信，因為有一些難以置信的定理[51]，其中一個定理位於第三頁的頁尾：
(若且唯若0 < a < b + 1/2時成立)
拉馬努金其他一些與無窮級數相關的成果也給哈代留下了深刻印象：
哈代發現，這些結果比高斯在積分方面的工作「有趣得多」。[52]
此外，拉馬努金還給出了漂亮的連分數：
其中是黃金分割。
讀完這封唐突來信後，哈代和他的同事利特爾伍德（J. E. Littlewood）議論道：「沒有一個定理可以放到世界上最高等的數學測試中。」即使自己就是當時著名的數學家，而且是其中幾個領域中的專家，他仍說：「（拉馬努金所寫下的許多東西）完全打敗了我」、「我從沒見過任何如此美麗的東西。」[53] 哈代稱拉馬努金是「一位最優秀的數學家，一位具有非凡獨創性和力量的人」。[51]:494–495
Remove ads
經歷起初的一些懷疑過後，1913年2月8日，哈代給拉馬努金寫了一封信，表達了對他工作的興趣，並補充說「我必須看看你某些論斷的證明」。[54]哈代聯繫了印度事務部，為拉馬努金的劍橋之行做計劃。出於宗教考慮，若到外國去，拉馬努金可能會喪失種姓，因此他拒絕離開祖國，父母也以同樣的理由反對他出國。[55] 三一學院前數學講師吉爾伯特·沃克在研究拉馬努金的成果時同樣表示驚嘆，並鼓勵這位年輕人到劍橋學習一段時間。[56] 後來，委員會同意在未來兩年內每月向拉馬努金提供75盧比的研究獎學金，供他在馬德拉斯大學學習和研究。[57] 拉馬努金在擔任研究生期間，繼續向《印度數學學會期刊》投稿。在拉馬努金拒絕前往英國後，哈代與拉馬努金的通信變得糟糕。哈代聘請了一位在馬德拉斯授課的同事E.H.內維爾來指導拉馬努金，並把他帶到英國。[58] 作為正統的婆羅門，拉馬努金諮詢了他的旅行星象，但後來，拉馬努金的母親做了個夢，其中家族女神告訴她不要阻攔兒子的行程。[59]1914年3月17日，拉馬努金乘船前往英國。[60]
1914年4月14日，拉馬努金在倫敦下船時，內維爾正開著車等候他。四天後，內維爾帶他去了位於劍橋切斯特頓路的家。拉馬努金立即開始與利特爾伍德和哈代合作。六周後，拉馬努金搬出了內維爾的家，搬到了惠威爾苑，離哈代的房間步行五分鐘。[61]哈代在前兩封信中已收到了拉馬努金提出的120個定理，但筆記中還有更多的結果和定理。哈代發現，有些結果和定理是錯誤的，有些已被發現，餘下的則是新突破。[62]
在劍橋，拉馬努金與哈代、利特爾伍德合作了近五年，並在那裡發表了部分研究成果。在艾狄胥的一次採訪中，哈代稱說他自己對數學最偉大的貢獻是發現了拉馬努金，拉馬努金的天賦至少可與數學巨人歐拉和雅可比（Carl Jacobi）相當。
哈代和拉馬努金的性格截然不同。他們的合作體現出不同文化、信仰和工作風格的碰撞。哈代堅信無神論，倡導數學求證及其嚴謹性；拉馬努金則是一位虔誠的印度教徒，盡力保持婆羅門的生活方式，因此十分依賴直覺和洞察力。
1916年3月，拉馬努金因其在高合數方面的研究成果，被授予研究文學學士學位（博士學位的前身）。[63][64]1917年12月6日，拉馬努金當選為倫敦數學學會院士。1918年5月2日，他當選為皇家學會院士。[65]1918年10月13日，他成為第一位當選劍橋大學三一學院院士的印度人。[66]
Remove ads
拉馬努金一生健康問題頻發。由於過度投入研究工作，他本就不佳的身體狀況在英國愈加惡化；難以恪守婆羅門的飲食要求，以及一戰時蔬菜的稀缺使病情變得更加嚴重。他被診斷出患有肺結核（Henderson, 1996年）以及嚴重的維生素缺乏症。
1917年末或1918年初，拉馬努金在倫敦地鐵站里墜軌，試圖自殺。蘇格蘭場以自殺未遂的罪名逮捕了他，但在哈代介入後，又將其釋放。[67][68]
拉馬努金於1919年返回貢伯戈訥姆，並於1920年逝世於當地，享年32歲。[26] 他送給這個世界最後的禮物是拉馬努金θ函數的發現。在他生命的最後幾天，儘管痛苦不堪，「他仍然繼續研究數學，一張接一張地填滿數字」，賈納基·阿馬爾回憶道。[69]
拉馬努金逝世後，妻子賈納姬搬到孟買，1950年回到清奈生活，並收養了一個兒子 W. Narayanan，在賈納姬晚年，她獲得了拉馬努金前雇主馬德拉斯港務局提供的終身養老金，以及印度國家科學院和泰米爾納德邦、安得拉邦、西孟加拉邦政府等方面提供的養老金。賈納姬繼續珍藏拉馬努金的記憶，並努力提高他的公眾知名度。許多著名數學家來訪印度期間都特意去看望她。1994年，賈納姬在位於特里普利凱恩的家中逝世。[70][26]
對於拉馬努金所患的疾病，1994年由楊格（Dr. D.A.B Young）進行的對拉馬努金的醫療紀錄和症狀的分析結論為更可能他有肝變形蟲病。拉馬努金在清奈待了很長時間進一步證實這點。雖然當時，這是很難診斷的疑症，但一旦診斷已是可治癒的（Berndt, 1998年）。
Remove ads
個性與精神生活
拉馬努金被描述為一個性格有些害羞和安靜的人，一個舉止優雅、品行端莊的人。[71]
拉馬努金終生過著婆羅門的生活。關於他實際信仰的觀點有很多說法：第一位傳記作者把他描述為一個嚴格正統的婆羅門，而哈代更相信他基本上是一個不可知論者。拉馬努金的宗教信仰被西方人浪漫化了，而印度傳記作者則誇大了——指的是他的信仰，而不是實踐。同時，他還評論了拉馬努金的嚴格素食主義。[72]
拉馬努金將他的理解歸功於他的家族女神納瑪姬莉（Namagiri：被視為Lakshmi吉祥天女的化身），並表示在他的工作中向她尋求靈感。他經常說：「一個方程對我沒有意義，除非它傳達了神的旨意。」賈納基在1984年曾表示，拉馬努金把大量時間花在數學上，以至於他不去寺廟。他沒時間吃飯，因此妻子和母親經常給他餵食。大多數歸因於他的宗教故事都源自他人。然而，他的正統信仰是毋庸置疑的。[73]
數學成就
拉馬努金天才地提出了大量公式，這些公式可供日後深入研究，並開闢新的研究方向。這些公式中最引人入勝的例子，包括π的無窮級數，其中之一如下所示：
該式基於負基本判別式： d = −4 × 58 = −232（其類數h(d) = 2）
與如下事實相關：
拉馬努金的π級數收斂速度極快，是計算π的最快算法之一。僅取級數的第一項，可得到π的近似值9801√2/4412，精確到小數點後六位；取前兩項時，精度可達14位小數（更一般的拉馬努金–佐藤級數也有類似性質）。
同時，他提出的許多恆等式推導出許多未知，如：
![{\displaystyle {\begin{aligned}&\left(1+2\sum _{n=1}^{\infty }{\frac {\cos(n\theta )}{\cosh(n\pi )}}\right)^{-2}+\left(1+2\sum _{n=1}^{\infty }{\frac {\cosh(n\theta )}{\cosh(n\pi )}}\right)^{-2}\\[6pt]={}&{\frac {2\Gamma ^{4}{\bigl (}{\frac {3}{4}}{\bigr )}}{\pi }}={\frac {8\pi ^{3}}{\Gamma ^{4}{\bigl (}{\frac {1}{4}}{\bigr )}}}\end{aligned}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/3affe3db147ab2c00c8ea31e9620380c20c7aafb)
對所有θ都成立，此處Γ(z)代表伽瑪函數。
比較恆等式兩邊θ之不同冪的係數，就可以得出雙曲正割的許多恆等式。
哈代這樣評論拉馬努金：
| “ | 他知識不足的程度跟知識的深厚都讓人很吃驚。他是能夠發現模方程和定理的人……到達前所未聞的地步，他對連分數的掌握……超出了世界上任何一個數學家，他自己發現了ζ函數的泛函方程和解析數論中的很多著名問題中級數的主要項；但他卻沒有聽說過雙周期函數或者柯西定理，對複變函數只有非常模糊的概念…… | ” |
Remove ads
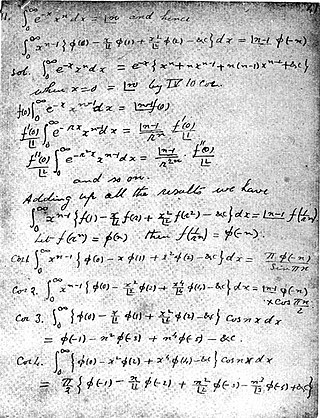
以下包括拉馬努金自己的發現，和與哈代的合作中發現和證明的定理
他也在下列領域做出重大突破和發現：
他的發現異常豐富；甚至很多在日後被發現，其內涵比原本乍看之下還要豐富許多。
雖然拉馬努金提出的很多命題都有資格被稱為拉馬努金（的）猜想，但其中一個特別有影響力，所以「拉馬努金猜想」通常指的是它。拉馬努金猜想斷定了拉馬努金τ函數的大小。這裡說的τ函數的生成函數是模判別式 Δ(q)（模形式理論中一種典型的尖形式（cusp form））。這個猜想在1973年由皮埃爾·德利涅證明的魏依猜想推論而得到證明，德利涅因此獲得1978年的菲爾茲獎。[2][74]
當拉馬努金還在印度時，他在活頁紙筆記上記錄了很多結果，但沒有記錄推導過程。有些人可能藉此認為拉馬努金並無證明這些結果的能力。但Berndt在對拉馬努金的評論中，感覺他肯定能夠對絕大部分的結果作出證明，只是沒有這樣做罷了。這種可能有幾種原因：那時的紙張並不便宜，拉馬努金在寫字石板上完成了他大部分的工作，然後只將結果轉移到紙上，這在當時是很常見的現象；拉馬努金也有可能受一本書影響——他大部分的高等數學知識的來源卡爾（G. S. Carr））《純數學和應用數學概要》（Synopsis of Pure and Applied Mathematics），這是卡爾用來教授數學的。它總結了幾千個結果，不帶證明的給出了它們。最後，可能拉馬努金認為他的工作只是給他自己的個人興趣用的；所以只記錄了結果。（Berndt, 1998）
第一本筆記有351頁，大約16個有某種組織的章節，以及一些無組織的材料。第二本筆記有256頁，散布在21章和100個無組織頁面中。第三本有33個未組織的頁面。
評價與紀念
拉馬努金可稱得上是印度過去千年中所出最偉大的數學家，他的直覺跳躍令當今的數學家都感到困惑與驚奇。在死後80多年，他的論文中所埋藏的秘密依然正在被挖掘。他的定理被應用到他活著的時候很難想像到的領域。[75]美國作家羅伯特·卡尼蓋爾所著傳記《知無涯者：拉馬努金傳》後被中國數學家、武漢大學前校長齊民友等翻譯成中文。
拉馬努金去世後的第二年，《自然》雜誌將他列入了「科學先驅日曆」。[76]
拉馬努金的家鄉泰米爾納德邦將12月22日（其生日）定為「國家信息技術日」。
2011年，在他誕辰125周年之際，印度政府宣布將每年的12月22日定為「國家數學日」。[77]時任印度總理曼莫漢·辛格也宣布，將2012年定為「國家數學年」，並將12月22日定為「印度國家數學日」 。
印度政府於1962年、2011年、2012年和2016年發行了印有拉馬努金肖像的郵票。[78]
1962
2011
2012
2016
軼事
拉馬努金病重，哈代前往探望，說道：「我搭計程車來，車牌號碼是，這數字真沒趣，希望不是不祥之兆。」拉馬努金答道：「不，這個數有趣得很。在所有可以用兩個立方數之和來表達而且有兩種表達方式的數之中，是最小的。」（即，後來這類數稱為的士數。）哈代引述利特爾伍德的話說：「每個正整數都是拉馬努金的朋友。」[79]
延伸閱讀
- Collected Papers of Srinivasa Ramanujan ISBN 0-8218-2076-1
- The Man Who Knew Infinity: A Life of the Genius Ramanujan by Robert Kanigel ISBN 0-671-75061-5（中譯本：《知無涯者：拉馬努金傳》；羅伯特‧卡尼蓋爾著；胡樂士、齊民友譯；上海科技教育出版社；2002）
參看
參考資料
外部連結
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads