热门问题
时间线
聊天
视角
正五胞體
来自维基百科,自由的百科全书
Remove ads
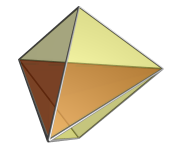
正五胞體是一種四維凸正多胞體,其展開為五個正四面體。正五胞體的投影的形狀可以想像成一個雙三角錐的兩頂點再加一條連線,或者是一個正四面體的四頂點連線至中心,在這裡,正五胞體作為正的正四面體面錐出現的。正五胞體有四個交面(等邊三角形),十條棱和五個頂點。正五胞體是最簡單的四維正多胞體(如同三角形是最簡單的多邊形)。
正五胞體是四維的正單體,這是一系列具有相同性質的多胞形的總稱,這一家族的特性在正五胞體上也體現出來了。五胞體是四維最簡單的多胞體,任何頂點數、棱數、面數、胞數比它小的多胞體都只能成為退化多胞體(即它們並不真正具有真實的、非零的超體積)。正五胞體的頂點排布是讓五個點在四維空間中兩兩間距離都相等的唯一方案。正五胞體同其它面為正三角形的多胞形一樣,具有穩定性,即如果正五胞體10條棱長都確定了,則正五胞體就被唯一確定了。
Remove ads
幾何性質
正五胞體作為一個單體,是自身對偶的。當它穿過三維空間時其截體積最大時,其截體是一個半正的正三稜柱。它的二胞角度數是cos-1(1/4),約等於75.52°。對於一個邊長為a的正五胞體,其超體積是,表體積是,高是。
若一個正五胞體的棱長為1,則其外接超球的半徑為,外中交超球(經過正五胞體各棱中點的三維超球)半徑為,內中交超球(經過正五胞體各面中心的三維超球)半徑為,內切超球半徑為。
Remove ads
對於一個邊長為2,中心在四維直角坐標系原點上的正五胞體,它的5個頂點坐標分別是
如果把正五胞體作為一個五維直角坐標系中的四維平面,則它的頂點坐標會簡單得多,為(0,0,0,0,1)或(0,1,1,1,1)的全排列(其中正五胞體棱長為),分別對應五維正軸體(正三十二超胞體)或五維半正方體。
Remove ads
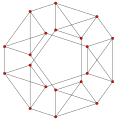
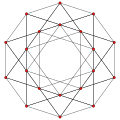
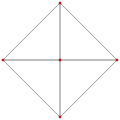
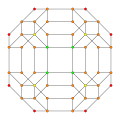
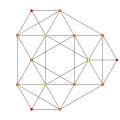
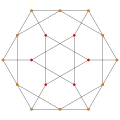
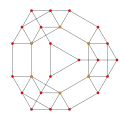
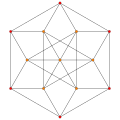
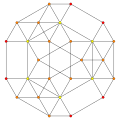
可視化
Remove ads
相關多胞體和堆砌
正五胞體是由考克斯特群[3,3,3]構造出來的9個半正多胞體中最簡單的一個。
Remove ads
參見
參考
Regular Convex Four-Dimensional Polytopes by David Fontaine,提供了部分關於正五胞體的幾何數據。
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads