Sabiranje

Sabiranje je osnovna aritmetička operacija, kojom saznajemo informaciju kad dvije ili više veličina (brojeva) skupimo zajedno, koliko ih ukupno ima. Sabirati možemo jabuke, kruške, lubenice, (sve su to cijeli brojevi), ali i tekućine koje se usipaju ili ističu iz spremnika, težine razne hrane i neprehrambenih artikala (decimalni brojevi).

3 + 2 = 5 sa jabukama, popularnim primjerom u školama^[1]

Matematički sabiranje je predstavljamo znakom plus +, npr. :${\displaystyle 1+2=3}$. Brojeve koje sabiramo nazivamo sabirnici, dok se rezultat koji nastaje sabiranjem naziva zbir.^[2]

Sabiranje je komutativno, što znači da je :${\displaystyle 1+2=2+1}$ , tj. možemo slobodno zamijeniti mjesta sabirnicima, a rezultat sabiranja se neće promijeniti.

Sabiranje je i asocijativno, jer vrijedi :${\displaystyle (1+2)+3=1+(2+3)}$

Kod sabiranja članova nekog niza koristi se veliko grčko slovo sigma:

${\displaystyle \sum _{i=1}^{n}x_{i}=x_{1}+x_{2}+x_{3}+\dots +x_{n-1}+x_{n},}$

što znači da sabiramo prvih n članova niza, od x₁ do x_n. Zbir članova Broj je apstraktni pojam koji koristimo za opis količina, bez brojeva ne bi bilo matematike.

Notacija i terminologija

Znak plus

Sabiranje se zapisuje korištenjem znaka plus "+" koji se stavlja između dva člana koji se sabiraju, to jest, u infiksnoj notaciji. Rezultat se izražava sa znakom jednakosti. Na primjer,

${\displaystyle 1+1=2}$ (verbalno, "jedan plus jedan jednako je dva")

${\displaystyle 2+2=4}$ (verbalno, "dva plus dva jednako je četiri")

${\displaystyle 5+4+2=11}$ (pogledajte "asocijativnost" ispod)

${\displaystyle 3+3+3+3=12}$ (pogledajte "množenje" ispod)

Osobine

Komutativnost

4 + 2 = 2 + 4 sa blokovima

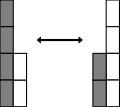
Sabiranje je komutativno, što znači da članovi, koji se sabiraju, mogu, međusobno, zamijeniti mjesta, a da rezultat ostane nepromijenjen. Simbolički, ako su a i b dva broja, tada vrijedi

${\displaystyle a+b=b+a}$

Asocijativnost

2+(1+3) = (2+1)+3 sa segnetntovanim štapovima

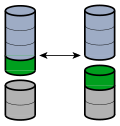
Još jedna osobina sabiranja je asocijativnost, koju dobijamo kada pokušamo definisati uzastopno sabiranje više članova zbira. Da li bi izraz

${\displaystyle a+b+c}$

trebao biti definisan kao

${\displaystyle (a+b)+c}$ ili :${\displaystyle a+(b+c)}$

Činjenica da je sabiranje asocijativno govori nam da je odabir definicije nebitan. Za bilo koja tri broja a, b i c, važi da je

${\displaystyle (a+b)+c=a+(b+c)}$

Na primjer

${\displaystyle (1+2)+3)=2+3=6=1+5=1+(2+3)}$ .

Nisu svi operatori asocijativni, tako da u izrazima sa ostalim operatorima, kao što je dijeljenje, važno je naznačiti redoslijed operacija.

Neutralni elemenat

Postoji jedan realan broj koji ako se sabere sa bilo kojim realnim brojem daje taj isti realan broj, tj. njegovo dodavanje na neki broj ne utiče na taj broj; taj realni broj se naziva neutral, i kod sabiranja realnih brojeva se obično predstavlja simbolom ${\displaystyle 0}$ i zove „nula“:

${\displaystyle \exists 0\in R,\forall x\in R,x+0=x}$

Inverzni elemenat

Za svaki uzeti realni broj, postoji njemu suprotan, označen sa znakom minus, koji kad se sabere sa tim brojem daje nulu; takav „suprotni“ broj nekog broja naziva se njegovim inverznim elementom:

${\displaystyle \forall x\in R,\exists {-x},x+(-x)=0}$

Uopćeno govoreći, sabiranje ne mora zadovoljavati sve navedene osobine za sve skupove nad kojim je definirano.

Naprimjer

sabiranje nad skupom cijelih brojeva ne zadovoljava uslove 3. i 4., sabiranje nad skupom ordinala ne zadovoljava uslove 1. i 4., itd.

Tablica sabiranja

+	1	2	3	4	5	6	7	8	9	10
1	2	3	4	5	6	7	8	9	10	11
2	3	4	5	6	7	8	9	10	11	12
3	4	5	6	7	8	9	10	11	12	13
4	5	6	7	8	9	10	11	12	13	14
5	6	7	8	9	10	11	12	13	14	15
6	7	8	9	10	11	12	13	14	15	16
7	8	9	10	11	12	13	14	15	16	17
8	9	10	11	12	13	14	15	16	17	18
9	10	11	12	13	14	15	16	17	18	19
10	11	12	13	14	15	16	17	18	19	20