Top Qs
Timeline
Chat
Perspective
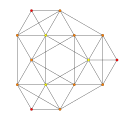
Cantellated 5-cell
From Wikipedia, the free encyclopedia
Remove ads
In four-dimensional geometry, a cantellated 5-cell is a convex uniform 4-polytope, being a cantellation (a 2nd order truncation, up to edge-planing) of the regular 5-cell.
Cantellated 5-cell
Summarize
Perspective
| Cantellated 5-cell | ||
|---|---|---|
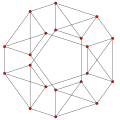
 Schlegel diagram with octahedral cells shown | ||
| Type | Uniform 4-polytope | |
| Schläfli symbol | t0,2{3,3,3} rr{3,3,3} | |
| Coxeter diagram | ||
| Cells | 20 | 5 5 10 |
| Faces | 80 | 50{3} 30{4} |
| Edges | 90 | |
| Vertices | 30 | |
| Vertex figure |  Square wedge | |
| Symmetry group | A4, [3,3,3], order 120 | |
| Properties | convex, isogonal | |
| Uniform index | 3 4 5 | |

The cantellated 5-cell or small rhombated pentachoron is a uniform 4-polytope. It has 30 vertices, 90 edges, 80 faces, and 20 cells. The cells are 5 cuboctahedra, 5 octahedra, and 10 triangular prisms. Each vertex is surrounded by 2 cuboctahedra, 2 triangular prisms, and 1 octahedron; the vertex figure is a nonuniform triangular prism.
Alternate names
- Cantellated pentachoron
- Cantellated 4-simplex
- (small) prismatodispentachoron
- Rectified dispentachoron
- Small rhombated pentachoron (Acronym: Srip) (Jonathan Bowers)
Configuration
Seen in a configuration matrix, all incidence counts between elements are shown. The diagonal f-vector numbers are derived through the Wythoff construction, dividing the full group order of a subgroup order by removing one mirror at a time.[1]
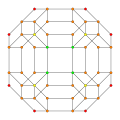
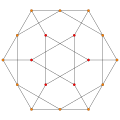
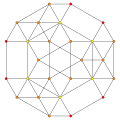
Images
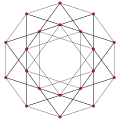
 Wireframe |
 Ten triangular prisms colored green |
 Five octahedra colored blue |
Coordinates
The Cartesian coordinates of the vertices of the origin-centered cantellated 5-cell having edge length 2 are:
The vertices of the cantellated 5-cell can be most simply positioned in 5-space as permutations of:
- (0,0,1,1,2)
This construction is from the positive orthant facet of the cantellated 5-orthoplex.
Related polytopes
The convex hull of two cantellated 5-cells in opposite positions is a nonuniform polychoron composed of 100 cells: three kinds of 70 octahedra (10 rectified tetrahedra, 20 triangular antiprisms, 40 triangular antipodiums), 30 tetrahedra (as tetragonal disphenoids), and 60 vertices. Its vertex figure is a shape topologically equivalent to a cube with a triangular prism attached to one of its square faces.
Remove ads
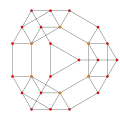
Cantitruncated 5-cell
Summarize
Perspective

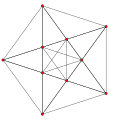
The cantitruncated 5-cell or great rhombated pentachoron is a uniform 4-polytope. It is composed of 60 vertices, 120 edges, 80 faces, and 20 cells. The cells are: 5 truncated octahedra, 10 triangular prisms, and 5 truncated tetrahedra. Each vertex is surrounded by 2 truncated octahedra, one triangular prism, and one truncated tetrahedron.
Configuration
Seen in a configuration matrix, all incidence counts between elements are shown. The diagonal f-vector numbers are derived through the Wythoff construction, dividing the full group order of a subgroup order by removing one mirror at a time.[2]
Alternative names
- Cantitruncated pentachoron
- Cantitruncated 4-simplex
- Great prismatodispentachoron
- Truncated dispentachoron
- Great rhombated pentachoron (Acronym: grip) (Jonathan Bowers)
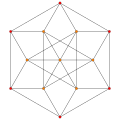
Images
 Stereographic projection with its 10 triangular prisms. |
Cartesian coordinates
The Cartesian coordinates of an origin-centered cantitruncated 5-cell having edge length 2 are:
These vertices can be more simply constructed on a hyperplane in 5-space, as the permutations of:
- (0,0,1,2,3)
This construction is from the positive orthant facet of the cantitruncated 5-orthoplex.
Related polytopes
A double symmetry construction can be made by placing truncated tetrahedra on the truncated octahedra, resulting in a nonuniform polychoron with 10 truncated tetrahedra, 20 hexagonal prisms (as ditrigonal trapezoprisms), two kinds of 80 triangular prisms (20 with D3h symmetry and 60 C2v-symmetric wedges), and 30 tetrahedra (as tetragonal disphenoids). Its vertex figure is topologically equivalent to the octahedron.
Remove ads
Related 4-polytopes
These polytopes are art of a set of 9 Uniform 4-polytopes constructed from the [3,3,3] Coxeter group.
References
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads






 ,
,  ...
...
















 ,
,  ...
...