Top Qs
Timeline
Chat
Perspective
Cantellated 5-orthoplexes
From Wikipedia, the free encyclopedia
Remove ads
In five-dimensional geometry, a cantellated 5-orthoplex is a convex uniform 5-polytope, being a cantellation of the regular 5-orthoplex.
There are 6 cantellation for the 5-orthoplex, including truncations. Some of them are more easily constructed from the dual 5-cube.
Remove ads
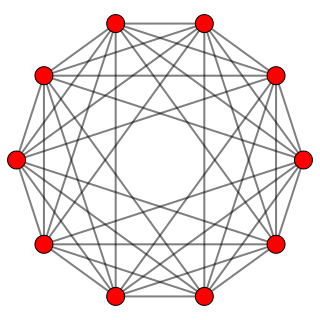
Cantellated 5-orthoplex
| Cantellated 5-orthoplex | ||
| Type | Uniform 5-polytope | |
| Schläfli symbol | rr{3,3,3,4} rr{3,3,31,1} | |
| Coxeter-Dynkin diagrams | ||
| 4-faces | 82 | 10 40 32 |
| Cells | 640 | 80 160 320 80 |
| Faces | 1520 | 640 320 480 80 |
| Edges | 1200 | 960 240 |
| Vertices | 240 | |
| Vertex figure | Square pyramidal prism | |
| Coxeter group | B5, [4,3,3,3], order 3840 D5, [32,1,1], order 1920 | |
| Properties | convex | |
Alternate names
- Cantellated 5-orthoplex
- Bicantellated 5-demicube
- Small rhombated triacontiditeron (Acronym: sart) (Jonathan Bowers)[1]
Coordinates
The vertices of the can be made in 5-space, as permutations and sign combinations of:
- (0,0,1,1,2)
Images
The cantellated 5-orthoplex is constructed by a cantellation operation applied to the 5-orthoplex.
Remove ads
Cantitruncated 5-orthoplex
Alternate names
- Cantitruncated pentacross
- Cantitruncated triacontiditeron (Acronym: gart) (Jonathan Bowers)[2]
Coordinates
Cartesian coordinates for the vertices of a cantitruncated 5-orthoplex, centered at the origin, are all sign and coordinate permutations of
- (±3,±2,±1,0,0)
Images
Remove ads
Related polytopes
These polytopes are from a set of 31 uniform 5-polytopes generated from the regular 5-cube or 5-orthoplex.
Notes
References
External links
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads