Log transformation (statistics)

In statistics, the log transformation is the application of the logarithmic function to each point in a data set—that is, each data point z_i is replaced with the transformed value y_i = log(z_i). The log transform is usually applied so that the data, after transformation, appear to more closely meet the assumptions of a statistical inference procedure that is to be applied, or to improve the interpretability or appearance of graphs.

The log transform is invertible, continuous, and monotonic. The transformation is usually applied to a collection of comparable measurements. For example, if we are working with data on peoples' incomes in some currency unit, it would be common to transform each person's income value by the logarithm function.

Motivation

Guidance for how data should be transformed, or whether a transformation should be applied at all, should come from the particular statistical analysis to be performed. For example, a simple way to construct an approximate 95% confidence interval for the population mean is to take the sample mean plus or minus two standard error units. However, the constant factor 2 used here is particular to the normal distribution, and is only applicable if the sample mean varies approximately normally. The central limit theorem states that in many situations, the sample mean does vary normally if the sample size is reasonably large. However, if the population is substantially skewed and the sample size is at most moderate, the approximation provided by the central limit theorem can be poor, and the resulting confidence interval will likely have the wrong coverage probability. Thus, when there is evidence of substantial skew in the data, it is common to transform the data to a symmetric distribution^[1] before constructing a confidence interval. If desired, the confidence interval can be constructed for statistics in the original scale, such as the median or the mean, by transforming back to the original scale using exponent (with some adjustments for CI for the mean), the inverse of the log transformation that was applied to the data.^[2][3] it is possible to estimate a quantile using different methods, build a CI for it, and then transform these back to the original scale so to have a CI for the quantile in the original scale. For example, it's possible to estimae the location of the median, after the log transformation, using the arithmetic mean. Then build CI for the median using a CI for the mean and transform the CI back to the original scale using exponent. That transformed CI is then a CI for the median, not the mean.

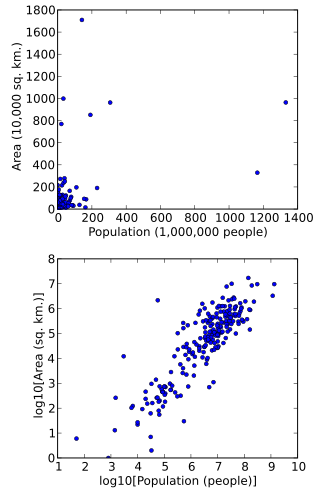
Data can also be transformed to make them easier to visualize. For example, suppose we have a scatterplot in which the points are the countries of the world, and the data values being plotted are the land area and population of each country. If the plot is made using untransformed data (e.g. square kilometers for area and the number of people for population), most of the countries would be plotted in tight cluster of points in the lower left corner of the graph. The few countries with very large areas and/or populations would be spread thinly around most of the graph's area. Simply rescaling units (e.g., to thousand square kilometers, or to millions of people) will not change this. However, following logarithmic transformations of both area and population, the points will be spread more uniformly in the graph.

Another reason for applying thr log data transformation is to improve interpretability, even if no formal statistical analysis or visualization is to be performed.

In regression

A scatterplot in which the areas of the sovereign states and dependent territories in the world are plotted on the vertical axis against their populations on the horizontal axis. The upper plot uses raw data. In the lower plot, both the area and population data have been transformed using the logarithm function.

See also: Linear regression § Assumptions

Data transformation may be used as a remedial measure to make data suitable for modeling with linear regression if the original data violates one or more assumptions of linear regression.^[4] For example, the simplest linear regression models assume a linear relationship between the expected value of Y (the response variable to be predicted) and each independent variable (when the other independent variables are held fixed). If linearity fails to hold, even approximately, it is sometimes possible to transform either the independent or dependent variables in the regression model to improve the linearity.^[5] For example, addition of quadratic functions of the original independent variables may lead to a linear relationship with expected value of Y, resulting in a polynomial regression model, a special case of linear regression.

Another assumption of linear regression is homoscedasticity, that is the variance of errors must be the same regardless of the values of predictors. If this assumption is violated (i.e. if the data is heteroscedastic), it may be possible to find a transformation of Y alone, or transformations of both X (the predictor variables) and Y, such that the homoscedasticity assumption (in addition to the linearity assumption) holds true on the transformed variables^[5] and linear regression may therefore be applied on these.

Yet another application of data transformation is to address the problem of lack of normality in error terms. Univariate normality is not needed for least squares estimates of the regression parameters to be meaningful (see Gauss–Markov theorem). However confidence intervals and hypothesis tests will have better statistical properties if the variables exhibit multivariate normality. Transformations that stabilize the variance of error terms (i.e. those that address heteroscedaticity) often also help make the error terms approximately normal.^[5][6]

Examples

Equation: ${\displaystyle Y=a+bX}$

Meaning: A unit increase in X is associated with an average of b units increase in Y.

Equation: ${\displaystyle \log(Y)=a+bX}$

(From exponentiating both sides of the equation: ${\displaystyle Y=e^{a}e^{bX}}$)

Meaning: A unit increase in X is associated with an average increase of b units in ${\displaystyle \log(Y)}$, or equivalently, Y increases on an average by a multiplicative factor of ${\displaystyle e^{b}\!}$. For illustrative purposes, if base-10 logarithm were used instead of natural logarithm in the above transformation and the same symbols (a and b) are used to denote the regression coefficients, then a unit increase in X would lead to a ${\displaystyle 10^{b}}$times increase in Y on an average. If b were 1, then this implies a 10-fold increase in Y for a unit increase in X

Equation: ${\displaystyle Y=a+b\log(X)}$

Meaning: A k-fold increase in X is associated with an average of ${\displaystyle b\times \log(k)}$units increase in Y. For illustrative purposes, if base-10 logarithm were used instead of natural logarithm in the above transformation and the same symbols (a and b) are used to denote the regression coefficients, then a tenfold increase in X would result in an average increase of ${\displaystyle b\times \log _{10}(10)=b}$ units in Y

Equation: ${\displaystyle \log(Y)=a+b\log(X)}$

(From exponentiating both sides of the equation: ${\displaystyle Y=e^{a}X^{b}}$)

Meaning: A k-fold increase in X is associated with a ${\displaystyle k^{b}}$multiplicative increase in Y on an average. Thus if X doubles, it would result in Y changing by a multiplicative factor of ${\displaystyle 2^{b}\!}$.^[7]

Relation to other transformations

The logarithm transformation is commonly used for positive data. The power transformation is a family of transformations that includes the logarithm, square root, and multiplicative inverse transformations as special cases. It is parameterized by a non-negative value λ and gives the log transformation when λ=0. To approach data transformation systematically, it is possible to use statistical estimation techniques to estimate the parameter λ in the power transformation, thereby identifying the transformation that is approximately the most appropriate in a given setting. Since the power transformation family also includes the identity transformation, this approach can also indicate whether it would be best to analyze the data without a transformation. In regression analysis, this approach is known as the Box–Cox transformation.

Occurrence and applications

See also: Log-normal_distribution § Occurrence_and_applications

A common situation where the log transformation is applied is when a value of interest ranges over several orders of magnitude. Many physical and social phenomena exhibit such behavior — incomes, species populations, galaxy sizes, and rainfall volumes, to name a few. Power transforms, and in particular the logarithm, can often be used to induce symmetry in such data. The logarithm is often favored because it is easy to interpret its result in terms of "fold changes".

The logarithm also has a useful effect on ratios. If we are comparing positive quantities X and Y using the ratio X / Y, then if X < Y, the ratio is in the interval (0,1), whereas if X > Y, the ratio is in the half-line (1,∞), where the ratio of 1 corresponds to equality. In an analysis where X and Y are treated symmetrically, the log-ratio log(X / Y) is zero in the case of equality, and it has the property that if X is K times greater than Y, the log-ratio is the equidistant from zero as in the situation where Y is K times greater than X (the log-ratios are log(K) and −log(K) in these two situations).

The log-normal distribution is important in the description of natural phenomena. Many natural growth processes are driven by the accumulation of many small percentage changes which become additive on a log scale. Under appropriate regularity conditions, the distribution of the resulting accumulated changes will be increasingly well approximated by a log-normal, as noted in the section above on "Multiplicative Central Limit Theorem". This is also known as Gibrat's law, after Robert Gibrat (1904–1980) who formulated it for companies.^[8] If the rate of accumulation of these small changes does not vary over time, growth becomes independent of size. Even if this assumption is not true, the size distributions at any age of things that grow over time tends to be log-normal.^{[citation needed]} Consequently, reference ranges for measurements in healthy individuals are more accurately estimated by assuming a log-normal distribution than by assuming a symmetric distribution about the mean.^{[citation needed]}

A second justification is based on the observation that fundamental natural laws imply multiplications and divisions of positive variables. Examples are the simple gravitation law connecting masses and distance with the resulting force, or the formula for equilibrium concentrations of chemicals in a solution that connects concentrations of educts and products. Assuming log-normal distributions of the variables involved leads to consistent models in these cases.

Specific examples are given in the following subsections.^[9] contains a review and table of log-normal distributions from geology, biology, medicine, food, ecology, and other areas.^[10] is a review article on log-normal distributions in neuroscience, with annotated bibliography.

Human behavior

• The length of comments posted in Internet discussion forums follows a log-normal distribution.^[11]
• Users' dwell time on online articles (jokes, news etc.) follows a log-normal distribution.^[12]
• The length of chess games tends to follow a log-normal distribution.^[13]
• Onset durations of acoustic comparison stimuli that are matched to a standard stimulus follow a log-normal distribution.^[14]

Biology and medicine

• Measures of size of living tissue (length, skin area, weight).^[15]
• Incubation period of diseases.^[16]
• Diameters of banana leaf spots, powdery mildew on barley.^[5]
• For highly communicable epidemics, such as SARS in 2003, if public intervention control policies are involved, the number of hospitalized cases is shown to satisfy the log-normal distribution with no free parameters if an entropy is assumed and the standard deviation is determined by the principle of maximum rate of entropy production.^[17]
• The length of inert appendages (hair, claws, nails, teeth) of biological specimens, in the direction of growth.^{[citation needed]}
• The normalised RNA-Seq readcount for any genomic region can be well approximated by log-normal distribution.
• The PacBio sequencing read length follows a log-normal distribution.^[18]
• Certain physiological measurements, such as blood pressure of adult humans (after separation on male/female subpopulations).^[19]
• Several pharmacokinetic variables, such as C_max, elimination half-life and the elimination rate constant.^[20]
• In neuroscience, the distribution of firing rates across a population of neurons is often approximately log-normal. This has been first observed in the cortex and striatum ^[21] and later in hippocampus and entorhinal cortex,^[22] and elsewhere in the brain.^[10][23] Also, intrinsic gain distributions and synaptic weight distributions appear to be log-normal^[24] as well.
• Neuron densities in the cerebral cortex, due to the noisy cell division process during neurodevelopment.^[25]
• In operating-rooms management, the distribution of surgery duration.
• In the size of avalanches of fractures in the cytoskeleton of living cells, showing log-normal distributions, with significantly higher size in cancer cells than healthy ones.^[26]

Chemistry

• Particle size distributions and molar mass distributions.
• The concentration of rare elements in minerals.^[27]
• Diameters of crystals in ice cream, oil drops in mayonnaise, pores in cocoa press cake.^[5]

Fitted cumulative log-normal distribution to annually maximum 1-day rainfalls, see distribution fitting

Hydrology

• In hydrology, the log-normal distribution is used to analyze extreme values of such variables as monthly and annual maximum values of daily rainfall and river discharge volumes.^[28]

The image on the right, made with CumFreq, illustrates an example of fitting the log-normal distribution to ranked annually maximum one-day rainfalls showing also the 90% confidence belt based on the binomial distribution.^[29]

The rainfall data are represented by plotting positions as part of a cumulative frequency analysis.

Social sciences and demographics

• In economics, there is evidence that the income of 97%–99% of the population is distributed log-normally.^[30] (The distribution of higher-income individuals follows a Pareto distribution).^[31]
• If an income distribution follows a log-normal distribution with standard deviation ${\displaystyle \sigma }$, then the Gini coefficient, commonly use to evaluate income inequality, can be computed as ${\displaystyle G=\operatorname {erf} \left({\frac {\sigma }{2}}\right)}$ where ${\displaystyle \operatorname {erf} }$ is the error function, since ${\displaystyle G=2\Phi \left({\frac {\sigma }{\sqrt {2}}}\right)-1}$, where ${\displaystyle \Phi (x)}$ is the cumulative distribution function of a standard normal distribution.
• In finance, in particular the Black–Scholes model, changes in the logarithm of exchange rates, price indices, and stock market indices are assumed normal^[32] (these variables behave like compound interest, not like simple interest, and so are multiplicative). However, some mathematicians such as Benoit Mandelbrot have argued ^[33] that log-Lévy distributions, which possesses heavy tails would be a more appropriate model, in particular for the analysis for stock market crashes. Indeed, stock price distributions typically exhibit a fat tail.^[34] The fat tailed distribution of changes during stock market crashes invalidate the assumptions of the central limit theorem.
• In scientometrics, the number of citations to journal articles and patents follows a discrete log-normal distribution.^[35][36]
• City sizes (population) satisfy Gibrat's Law.^[37] The growth process of city sizes is proportionate and invariant with respect to size. From the central limit theorem therefore, the log of city size is normally distributed.
• The number of sexual partners appears to be best described by a log-normal distribution.^[38]

Technology

• In reliability analysis, the log-normal distribution is often used to model times to repair a maintainable system.^[39]
• In wireless communication, "the local-mean power expressed in logarithmic values, such as dB or neper, has a normal (i.e., Gaussian) distribution."^[40] Also, the random obstruction of radio signals due to large buildings and hills, called shadowing, is often modeled as a log-normal distribution.
• Particle size distributions produced by comminution with random impacts, such as in ball milling.^[41]
• The file size distribution of publicly available audio and video data files (MIME types) follows a log-normal distribution over five orders of magnitude.^[42]
• File sizes of 140 million files on personal computers running the Windows OS, collected in 1999.^[43][11]
• Sizes of text-based emails (1990s) and multimedia-based emails (2000s).^[11]
• In computer networks and Internet traffic analysis, log-normal is shown as a good statistical model to represent the amount of traffic per unit time. This has been shown by applying a robust statistical approach on a large groups of real Internet traces. In this context, the log-normal distribution has shown a good performance in two main use cases: (1) predicting the proportion of time traffic will exceed a given level (for service level agreement or link capacity estimation) i.e. link dimensioning based on bandwidth provisioning and (2) predicting 95th percentile pricing.^[44]
• in physical testing when the test produces a time-to-failure of an item under specified conditions, the data is often best analyzed using a lognormal distribution.^[45][46]

See also

• Data transformation (statistics)
• Log-normal distribution
• Log–log plot
• Variance-stabilizing transformation
• Box–Cox distribution
• Power transform
• Logarithm
• Logarithmic scale
• Delta method (for exp of approx normal distributions)
• Median test
• Laplace's approximation
• Arcsin
• Feature engineering
• Logit
• Nonlinear regression § Transformation
• Pearson correlation coefficient
• Power transform (Box–Cox)
• Wilson–Hilferty transformation
• Whitening transformation