
Inversa hiperbola funkcio
From Wikipedia, the free encyclopedia
En matematiko, inversaj hiperbolaj funkcioj estas retroĵetoj de hiperbolaj funkcioj.
 ,
,  ...
...| Hiperbola funkcio | Inversa hiperbola funkcio | |||
|---|---|---|---|---|
| Nomo | Skribmaniero | Difino | Nomo | Skribmaniero |
| Hiperbola sinuso | y=sinh x aŭ y=sh x |  |
Inversa hiperbola sinuso | u=arcsinh v aŭ u=arsinh v aŭ u=asinh v aŭ u=arsh v |
| Hiperbola kosinuso | y=cosh x aŭ y=ch x |  |
Inversa hiperbola kosinuso | u=arccosh v aŭ u=arcosh v aŭ u=acosh v aŭ u=arch v |
| Hiperbola tangento | y=tanh x aŭ th x |  |
Inversa hiperbola tangento | u=arctanh v aŭ u=artanh v aŭ u=atanh v |
| Hiperbola kotangento | y=coth x aŭ cth x |  |
Inversa hiperbola kotangento | u=arccoth v aŭ u=arcoth v aŭ u=acoth v |
| Hiperbola sekanto | y=sech x |  |
Inversa hiperbola sekanto | u=arcsech v aŭ u=arsech v aŭ u=asech v |
| Hiperbola kosekanto | y=csch |  |
Inversa hiperbola kosekanto | u=arccsch v aŭ u=arcsch v aŭ u=acsch v |
 arsinh x |
 arcosh x |
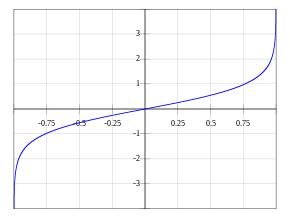 artanh x |
 arcoth x |
 arsech x |
 arcsch x |

Ili estas nomataj ankaŭ kiel areaj hiperbolaj funkcioj, ĉar ili komputas areon de sektoro de la unua hiperbolo x2-y2 = 1, simile al tio kiel inversaj trigonometriaj funkcioj komputas longon de arko de la unuobla cirklo x2+y2 = 1.
La kutimaj simboloj por ili (ekzemple por hiperbola sinuso) estas kiel arsinh, arcsinh aŭ asinh (en komputiko). Ankaŭ skribmaniero kiel sinh−1 (x) estas uzata. La simboloj komenciĝantaj de "arc" (arcsinh, ...) estas kutime uzita, sed fakte ili estas misnomaĵoj ĉar la prefikso "arc" devenas de vorto arko analoge al inversaj trigonometriaj funkcioj, sed inversaj hiperbolaj funkcioj ne kalkulas arkon. La prefikso "ar" devenas de vorto areo kaj respektivas la realan kalkuladon.
Sur reelaj nombroj, nur sinh, tanh, coth kaj csch permesas retroĵetadon kun certa ricevo de la originala valoro (tiel por ĉiu reela x, ekzemple arsinh (sinh x)=x). cosh kaj sech prenas (sur reela domajno) preskaŭ ĉiun eblan valoron je du malsamaj argumentoj, sed la ĉefa valoro de inversa funkcio redonas nur unuon el la du eblaj variantoj.
Pro tio ke ĉiuj hiperbolaj funkcioj estas periodaj kun kompleksa periodo 2πi (πi por hiperbola tangento kaj hiperbola kotangento), apliko de la inversa funkcio kun preno de la ĉefa valoro (vidu sube) ne ĉiam donas la originalan valoron. Tiel la inversaj funkcioj estas multvaloraj funkcioj