Produto vectorial

En matemática, o produto vectorial é unha operación binaria sobre vectores nun espazo vectorial. Pode ser denominado tamén como produto externo ou produto cruz. O seu resultado difire do produto escalar por ser tamén un vector, ao contrario dun escalar. O seu principal uso baséase no feito de que o resultado dun produto vectorial é sempre perpendicular a ambos os vectores orixinais, así como que o módulo do vector resultante do produto é a área do paralelogramo que conformarían os vectores do produto.

Produto vectorial.

Definición

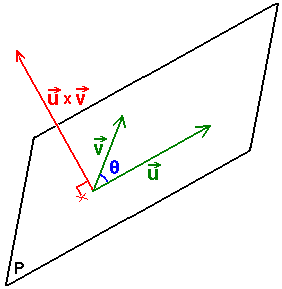
A notación do produto vectorial entre dous vectores a e b é a × b (en manuscritos, algúns matemáticos escriben a ∧ b para evitar a confusión coa x). Podemos definilo como:

${\displaystyle \mathbf {a} \times \mathbf {b} =\mathbf {n} \left|\mathbf {a} \right|\left|\mathbf {b} \right|sen\theta }$

onde θ é a medida do ángulo entre a e b (0° ≤ θ ≤ 180°) no plano definido polos dous vectores, e n é o vector unitario perpendicular a tanto a canto b.

O problema con esta definición é que existen dous vectores unitarios que son perpendiculares a a e b simultaneamente: se n é perpendicular, entón −n tamén o é.

O resultado correcto depende da orientación do espazo vectorial, i.e. da quiralidade do sistema de coordenadas (i, j, k). O produto vectorial a × b é definido de tal forma que (a, b, a × b) se torna destro se (i, j, k) é "a dereitas" ou zurdo se (i, j, k) é "a esquerdas".

Unha forma fácil de calcular a dirección do vector resultante é a "regra da man dereita". Se un sistema de coordenadas é destro, basta apuntar o indicador na dirección do primeiro operando e o dedo medio na dirección do segundo operando. Desta forma, o vector resultante é dado pola dirección do polgar.

Sexan dous vectores ${\displaystyle \mathbf {a} }$ e ${\displaystyle \mathbf {b} }$ no espazo vectorial ${\displaystyle \mathbb {R} ^{3}}$. O produto vectorial entre ${\displaystyle \mathbf {a} \,}$ e ${\displaystyle \mathbf {b} \,}$ dá como resultado un novo vector, ${\displaystyle \mathbf {c} \,}$. Para definir este novo vector é necesario especificar o seu módulo e dirección:

• O módulo de ${\displaystyle \mathbf {c} \,}$ está dado por

${\displaystyle c=a\,b\,\sin \theta }$

onde θ é o ángulo determinado polos vectores a e b.

• A dirección do vector c, que é ortogonal a a e ortogonal a b, está dada pola regra da man dereita.

Computación

Notación de coordenadas

Base estándar vectores i, j, k e compoñentes vectoriais de a, denotados aquí a_x, a_y, a_z

Se ${\displaystyle (\mathbf {\color {blue}{i}} ,\mathbf {\color {red}{j}} ,\mathbf {\color {green}{k}} )}$ é unha base ortonormal orientada positivamente, os vectores da base cumpren as seguintes igualdades^[1]

${\displaystyle {\begin{alignedat}{2}\mathbf {\color {red}{j}} &\times \mathbf {\color {blue}{i}} &&=-\mathbf {\color {green}{k}} \\\mathbf {\color {green}{k}} &\times \mathbf {\color {red}{j}} &&=-\mathbf {\color {blue}{i}} \\\mathbf {\color {blue}{i}} &\times \mathbf {\color {green}{k}} &&=-\mathbf {\color {red}{j}} \end{alignedat}}}$

Unha regra mnemotécnica para estas fórmulas é que se poden deducir de calquera outra delas mediante unha permutación cíclica dos vectores base. Esta mnemotécnica aplícase tamén a moitas fórmulas que se dan neste artigo.

A anticonmutatividade do produto vectorial implica que

${\displaystyle {\begin{alignedat}{2}\mathbf {\color {red}{j}} &\times \mathbf {\color {blue}{i}} &&=-\mathbf {\color {green}{k}} \\\mathbf {\color {green}{k}} &\times \mathbf {\color {red}{j}} &&=-\mathbf {\color {blue}{i}} \\\mathbf {\color {blue}{i}} &\times \mathbf {\color {green}{k}} &&=-\mathbf {\color {red}{j}} \end{alignedat}}}$

A anticomutatividade do produto vectorial (e a evidente falta de independencia linear) tamén implica que

${\displaystyle \mathbf {\color {blue}{i}} \times \mathbf {\color {blue}{i}} =\mathbf {\color {red}{j}} \times \mathbf {\color {red}{j}} =\mathbf {\color {green}{k}} \times \mathbf {\color {green}{k}} =\mathbf {0} }$ (o vector cero).

Estas igualdades, xunto coa distributividade e a linearidade do produto vectorial (aínda que ningunha das dúas se deduce facilmente da definición anterior), son suficientes para determinar o produto vectorial de dous vectores calquera a e b. Cada vector pódese definir como a suma de tres compoñentes ortogonais paralelos aos vectores de base estándar:

${\displaystyle {\begin{alignedat}{3}\mathbf {a} &=a_{1}\mathbf {\color {blue}{i}} &&+a_{2}\mathbf {\color {red}{j}} &&+a_{3}\mathbf {\color {green}{k}} \\\mathbf {b} &=b_{1}\mathbf {\color {blue}{i}} &&+b_{2}\mathbf {\color {red}{j}} &&+b_{3}\mathbf {\color {green}{k}} \end{alignedat}}}$

O seu produto vectorial a × b pódese expandir usando a distributividade:

${\displaystyle {\begin{aligned}\mathbf {a} \times \mathbf {b} ={}&(a_{1}\mathbf {\color {blue}{i}} +a_{2}\mathbf {\color {red}{j}} +a_{3}\mathbf {\color {green}{k}} )\times (b_{1}\mathbf {\color {blue}{i}} +b_{2}\mathbf {\color {red}{j}} +b_{3}\mathbf {\color {green}{k}} )\\={}&a_{1}b_{1}(\mathbf {\color {blue}{i}} \times \mathbf {\color {blue}{i}} )+a_{1}b_{2}(\mathbf {\color {blue}{i}} \times \mathbf {\color {red}{j}} )+a_{1}b_{3}(\mathbf {\color {blue}{i}} \times \mathbf {\color {green}{k}} )+{}\\&a_{2}b_{1}(\mathbf {\color {red}{j}} \times \mathbf {\color {blue}{i}} )+a_{2}b_{2}(\mathbf {\color {red}{j}} \times \mathbf {\color {red}{j}} )+a_{2}b_{3}(\mathbf {\color {red}{j}} \times \mathbf {\color {green}{k}} )+{}\\&a_{3}b_{1}(\mathbf {\color {green}{k}} \times \mathbf {\color {blue}{i}} )+a_{3}b_{2}(\mathbf {\color {green}{k}} \times \mathbf {\color {red}{j}} )+a_{3}b_{3}(\mathbf {\color {green}{k}} \times \mathbf {\color {green}{k}} )\\\end{aligned}}}$

Isto pódese interpretar como a descomposición de a × b na suma de nove produtos vectoriais máis simples que involucran vectores aliñados con i, j ou k. Cada un destes nove produtos vecotriais opera en dous vectores que son fáciles de manexar xa que son paralelos ou ortogonais entre si. A partir desta descomposición, empregando as igualdades mencionada anteriormente e recompilando termos semellantes, obtemos:

${\displaystyle {\begin{aligned}\mathbf {a} \times \mathbf {b} ={}&\quad \ a_{1}b_{1}\mathbf {0} +a_{1}b_{2}\mathbf {\color {green}{k}} -a_{1}b_{3}\mathbf {\color {red}{j}} \\&-a_{2}b_{1}\mathbf {\color {green}{k}} +a_{2}b_{2}\mathbf {0} +a_{2}b_{3}\mathbf {\color {blue}{i}} \\&+a_{3}b_{1}\mathbf {\color {red}{j}} \ -a_{3}b_{2}\mathbf {\color {blue}{i}} \ +a_{3}b_{3}\mathbf {0} \\={}&(a_{2}b_{3}-a_{3}b_{2})\mathbf {\color {blue}{i}} +(a_{3}b_{1}-a_{1}b_{3})\mathbf {\color {red}{j}} +(a_{1}b_{2}-a_{2}b_{1})\mathbf {\color {green}{k}} \\\end{aligned}}}$

o que significa que as tres compoñentes escalares do vector resultante s = s₁i + s₂j + s₃k = a × b son

${\displaystyle {\begin{aligned}s_{1}&=a_{2}b_{3}-a_{3}b_{2}\\s_{2}&=a_{3}b_{1}-a_{1}b_{3}\\s_{3}&=a_{1}b_{2}-a_{2}b_{1}\end{aligned}}}$

Usando vector columnas, podemos representar o mesmo resultado do seguinte xeito:

${\displaystyle {\begin{bmatrix}s_{1}\\s_{2}\\s_{3}\end{bmatrix}}={\begin{bmatrix}a_{2}b_{3}-a_{3}b_{2}\\a_{3}b_{1}-a_{1}b_{3}\\a_{1}b_{2}-a_{2}b_{1}\end{bmatrix}}}$

Produto vectorial usando matrices

Sexan ${\displaystyle \mathbf {u} =u_{x}\mathbf {i} +u_{y}\mathbf {j} +u_{z}\mathbf {k} }$ e ${\displaystyle \mathbf {v} =v_{x}\mathbf {i} +v_{y}\mathbf {j} +v_{z}\mathbf {k} }$ dous vectores concorrentes de ${\displaystyle \mathbb {R} ^{3}}$, o espazo afín tridimensional segundo a base anterior.

Defínese o produto ${\displaystyle \times$ :\mathbb {R} ^{3}\times \mathbb {R} ^{3}\longrightarrow \mathbb {R} ^{3}} , e escríbese ${\displaystyle \mathbf {u} \times \mathbf {v} }$, como o vector:

${\displaystyle \mathbf {u} \times \mathbf {v} ={\begin{vmatrix}u_{y}&u_{z}\\v_{y}&v_{z}\\\end{vmatrix}}\mathbf {i} -{\begin{vmatrix}u_{x}&u_{z}\\v_{x}&v_{z}\\\end{vmatrix}}\mathbf {j} +{\begin{vmatrix}u_{x}&u_{y}\\v_{x}&v_{y}\\\end{vmatrix}}\mathbf {k} }$

No que

${\displaystyle {\begin{vmatrix}a&c\\b&d\\\end{vmatrix}}=a\cdot d-b\cdot c}$, é o determinante de orde 2.

Ou usando unha notación máis compacta, mediante o desenvolvemento pola primeira fila dun determinante simbólico de orde 3 (simbólico xa que os termos da primeira fila non son escalares):

${\displaystyle \mathbf {u} \times \mathbf {v} ={\begin{vmatrix}\mathbf {i} &\mathbf {j} &\mathbf {k} \\u_{x}&u_{y}&u_{z}\\v_{x}&v_{y}&v_{z}\\\end{vmatrix}}={\begin{vmatrix}u_{y}&u_{z}\\v_{y}&v_{z}\\\end{vmatrix}}\cdot \mathbf {i} -{\begin{vmatrix}u_{x}&u_{z}\\v_{x}&v_{z}\\\end{vmatrix}}\cdot \mathbf {j} +{\begin{vmatrix}u_{x}&u_{y}\\v_{x}&v_{y}\\\end{vmatrix}}\cdot \mathbf {k} }$

Que dá orixe á chamada regra da man dereita ou regra do sacarrollas: xirando o primeiro vector cara ao segundo polo ángulo máis pequeno, a dirección de ${\displaystyle \mathbf {u} \times \mathbf {v} }$ é o dun sacarrollas que xire na mesma dirección.

Exemplo

O produto vectorial dos vectores ${\displaystyle \mathbf {a} =(2,0,1)}$ e ${\displaystyle \mathbf {b} =(1,-1,3)}$ calcúlase do seguinte xeito:

${\displaystyle \mathbf {a} \times \mathbf {b} ={\begin{vmatrix}\mathbf {i} &\mathbf {j} &\mathbf {k} \\2&0&1\\1&-1&3\\\end{vmatrix}}}$

Expandindo o determinante:

${\displaystyle \mathbf {a} \times \mathbf {b} =\mathbf {i} {\begin{vmatrix}0&1\\-1&3\\\end{vmatrix}}-\mathbf {j} {\begin{vmatrix}2&1\\1&3\\\end{vmatrix}}+\mathbf {k} {\begin{vmatrix}2&0\\1&-1\\\end{vmatrix}}=\mathbf {i} -5\mathbf {j} -2\mathbf {k} }$

Pode verificarse facilmente que ${\displaystyle \mathbf {a} \times \mathbf {b} }$ é ortogonal aos vectores ${\displaystyle \mathbf {a} }$ e ${\displaystyle \mathbf {b} }$ efectuando o produto escalar e verificando que este é nulo (condición de perpendicularidade de vectores).

Usando os tensores de Levi-Civita

• En calquera base, o produto vectorial ${\displaystyle a\times b}$ vén dado pola fórmula tensorial ${\displaystyle E_{ijk}a^{i}b^{j}}$ onde ${\displaystyle E_{ijk}}$ é o tensor covariante Levi-Civita (observamos a posición dos índices). Isto corresponde á fórmula intrínseca dada aquí.
• Nunha base ortonormal que ten a mesma orientación que o espazo, ${\displaystyle a\times b}$ vén dado pola fórmula pseudotensorial ${\displaystyle \varepsilon _{ijk}a^{i}b^{j}}$ onde ${\displaystyle \varepsilon _{ijk}}$ é o símbolo de Levi-Civita (que é un pseudotensor). Esa é a fórmula utilizada para a física cotiá, pero só funciona para esta elección especial de base.
• En calquera base ortonormal, ${\displaystyle a\times b}$ vén dado pola fórmula pseudotensorial ${\displaystyle (-1)^{B}\varepsilon _{ijk}a^{i}b^{j}}$ onde ${\displaystyle (-1)^{B}=\pm 1}$ indica se a base ten a mesma orientación que o espazo ou non.

A última fórmula evita ter que mudar a orientación do espazo cando invertimos unha base ortonormal.

Como produto exterior

O produto vectorial en relación co produto exterior. En vermello están o vector unitario ortogonal e o bivector unitario "paralelo".

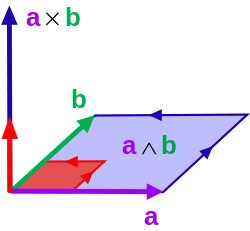
O produto vectorial pódese definir en termos do produto exterior. Pódese xeneralizar a un produto exterior noutras dimensións que non sexan tres.^[2] Esta xeneralización permite unha interpretación xeométrica natural do produto vectorial. En álxebra exterior o produto exterior de dous vectores é un bivector. Un bivector é un elemento plano orientado, do mesmo xeito que un vector é un elemento de liña orientado. Dados dous vectores a e b, pódese ver o bivector a ∧ b como o paralelogramo orientado abranguido por a e b. O produto vectorial obtense entón tomando a estrela de Hodge do bivector a ∧ b, mapeando 2-vectores a vectores:

${\displaystyle a\times b=\star (a\wedge b).}$

Isto pódese considerar como o elemento multidimensional orientado "perpendicular" ao bivector. Nun espazo d-dimensional, a estrela de Hodge toma un k-vector a un (d–k)-vector; polo tanto, só en d = 3 dimensións o resultado é un elemento de dimensión un (3–2 = 1), é dicir, un vector. Por exemplo, en 4 dimensións, o produto vectorial de dous vectores ten a dimensión 4–2 = 2, o que dá lugar a un bivector. Polo tanto, só en tres dimensións o produto vectorial define unha estrutura alxébrica para multiplicar vectores.