អនុគមន៍ត្រីកោណមាត្រច្រាស់

នៅក្នុងគណិតវិទ្យា​ អនុគមន៍ត្រីកោណមាត្រច្រាស់ ឬអនុគមន៍ស៊ីក្លូមេទ្រីក គឺជាអនុគមន៍ច្រាស់នៃអនុគមន៍ត្រីកោណមាត្រ។ អនុគមន៍ច្រាស់សំខាន់ៗត្រូវបានដាក់បញ្ចូលក្នុងតារាងខាងក្រោម។

ឈ្មោះ	កំនត់សំគាល់ទូទៅ	និយមន័យ	ដែនកំនត់នៃ x ចំពោះលទ្ធផលពិត	ចន្លោះនៃតំលៃគោលទូទៅ
អាកស៊ីនុស	y = arcsin(x)	x = sin(y)	ពី −1 ដល់ +1	−π/2 ≤ y ≤ π/2
អាកកូស៊ីនុស	y = arccos(x)	x = cos(y)	ពី −1 ដល់ +1	0 ≤ y ≤ π
អាកតង់សង់	y = arctan(x)	x = tan(y)	ទាំងអស់	−π/2 < y < π/2
អាកកូតង់សង់	y = arccot(x)	x = cot(y)	ទាំងអស់	0 < y < π
អាកសេកង់	y = arcsec(x)	x = sec(y)	ពី −∞ ដល់ −1 ឬ ពី 1 ដល់ ∞	0 ≤ y < π/2 ឬ π/2 < y ≤ π
អាកកូសេកង់	y = arccsc(x)	x = csc(y)	ពី −∞ ដល់ −1 ឬ ពី 1 ដល់ ∞	−π/2 ≤ y < 0 ឬ 0 < y ≤ π/2

ប្រសិនបើ x ជាចំនួនកុំផ្លិច នោះដែនកំនត់នៃ y អាចអនុវត្តបានតែចំពោះផ្នែកពិតប៉ុណ្ណោះ។

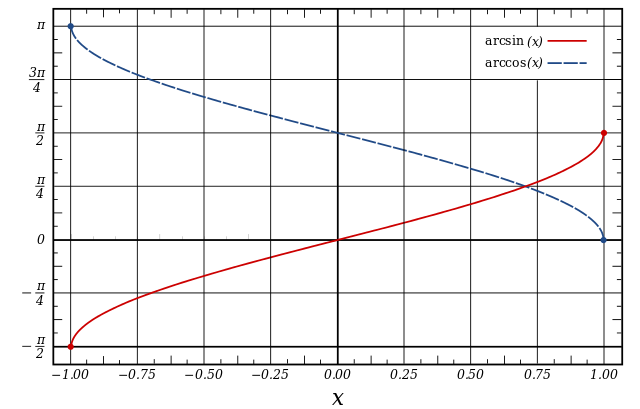
កំនត់សំគាល់ ${\displaystyle \sin ^{-1},\cos ^{-1}}$ ជាដើម ជាញឹកញាប់ត្រូវបានគេប្រើប្រាស់ចំពោះ arcsin, arccos ជាដើម។ ប៉ន្តែការសន្មតនេះវាអាចធ្វើអោយមានការភាន់ច្រលំជាមួយ​កន្សោមមួយចំនួនដូចជា ${\displaystyle sin^{2}(x)\,}$ ។

តំលៃគោលនៃ អនុគមន៍ f(x) = arcsin(x) និង f(x) = arccos(x) នៅក្នុងប្លង់ដេកាត

តំលៃគោលនៃ អនុគមន៍ f(x) = arctan(x) និង f(x) = arccot(x) នៅក្នុងប្លង់ដេកាត

តំលៃគោលនៃ អនុគមន៍ f(x) = arcsec(x) និង f(x) = arccsc(x) នៅក្នុងប្លង់ដេកាត

ទំនាក់ទំនងក្នុងអនុគមន៍ត្រីកោណមាត្រច្រាស់

<math>\arccos x = \frac{\pi}{2} - \arcsin x </math>

<math>\arccot x = \frac{\pi}{2} - \arctan x </math>

<math>\arccsc x = \frac{\pi}{2} - \arcsec x </math>

ចំពោះមុំផ្ទុយ

<math>\arcsin (-x) = - \arcsin x \!</math>

<math>\arccos (-x) = \pi - \arccos x \!</math>

<math>\arctan (-x) = - \arctan x \!</math>

<math>\arccot (-x) = \pi - \arccot x \!</math>

<math>\arcsec (-x) = \pi - \arcsec x \!</math>

<math>\arccsc (-x) = - \arccsc x \!</math>

ចំពោះមុំចំរាស់:

<math>\arccos \frac{1}{x} \,= \arcsec x </math>

<math>\arcsin \frac{1}{x} \,= \arccsc x </math>

<math>\arctan \frac{1}{x} = \frac{\pi}{2} - \arctan x =\arccot x, \ </math> ប្រសិនបើ <math>\ x > 0</math>

<math>\arctan \frac{1}{x} = -\frac{\pi}{2} - \arctan x = -\pi + \arccot x, \ </math> ប្រសិនបើ <math>\ x < 0</math>

<math>\arccot \frac{1}{x} = \frac{\pi}{2} - \arccot x =\arctan x, \ </math>

ដេរីវេនៃអនុគមន៍ត្រីកោណមាត្រច្រាស់

${\displaystyle {\begin{aligned}{\frac {d}{dx}}\arcsin x&{}={\frac {1}{\sqrt {1-x^{2}}}}\\{\frac {d}{dx}}\arccos x&{}={\frac {-1}{\sqrt {1-x^{2}}}}\\{\frac {d}{dx}}\arctan x&{}={\frac {1}{1+x^{2}}}\\{\frac {d}{dx}}\operatorname {arccot} x&{}={\frac {-1}{1+x^{2}}}\\{\frac {d}{dx}}\operatorname {arcsec} x&{}={\frac {1}{x^{2}\,{\sqrt {1-{1 \over {x^{2}}}}}}}\\{\frac {d}{dx}}\operatorname {arccsc} x&{}={\frac {-1}{x^{2}\,{\sqrt {1-{1 \over {x^{2}}}}}}}\end{aligned}}}$

ចំពោះតែតំលៃនៃ ${\displaystyle x\,}$៖

${\displaystyle {\begin{aligned}{\frac {d}{dx}}\operatorname {arcsec} x&{}={\frac {1}{|x|\,{\sqrt {x^{2}-1}}}};\qquad |x|>1\\{\frac {d}{dx}}\operatorname {arccsc} x&{}={\frac {-1}{|x|\,{\sqrt {x^{2}-1}}}};\qquad |x|>1\end{aligned}}}$

ចំពោះដេរីវេធម្មតា៖ ប្រសិនបើ ${\displaystyle \theta =\arcsin x\!}$ យើងបាន៖

${\displaystyle {\frac {d\arcsin x}{dx}}={\frac {d\theta }{d\sin \theta }}={\frac {1}{\cos \theta }}={\frac {1}{\sqrt {1-\sin ^{2}\theta }}}={\frac {1}{\sqrt {1-x^{2}}}}}$

អនុគមន៍ត្រីកោណមាត្រច្រាស់ជាកន្សោមអាំងតេក្រាល

${\displaystyle {\begin{aligned}\arcsin x&{}=\int _{0}^{x}{\frac {1}{\sqrt {1-z^{2}}}}\,dz,\qquad |x|\leq 1\\\arccos x&{}=\int _{x}^{1}{\frac {1}{\sqrt {1-z^{2}}}}\,dz,\qquad |x|\leq 1\\\arctan x&{}=\int _{0}^{x}{\frac {1}{z^{2}+1}}\,dz,\\\operatorname {arccot} x&{}=\int _{x}^{\infty }{\frac {1}{z^{2}+1}}\,dz,\\\operatorname {arcsec} x&{}=\int _{1}^{x}{\frac {1}{z{\sqrt {z^{2}-1}}}}\,dz,\qquad x\geq 1\\\operatorname {arccsc} x&{}=\int _{x}^{\infty }{\frac {1}{z{\sqrt {z^{2}-1}}}}\,dz,\qquad x\geq 1\end{aligned}}}$

នៅពេលស្មើ 1 នោះអាំងតេក្រាលដែលមានដែនកំនត់កំនត់ ជាimproper integral ប៉ុន្តែវានៅតែអាចកំនត់បាន។

ស៊េរីអានន្ត

${\displaystyle {\begin{aligned}\arcsin z&{}=z+\left({\frac {1}{2}}\right){\frac {z^{3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {z^{5}}{5}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {z^{7}}{7}}+\cdots \\&{}=\sum _{n=0}^{\infty }\left({\frac {(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {z^{2n+1}}{(2n+1)}};\qquad |z|\leq 1\end{aligned}}}$

${\displaystyle {\begin{aligned}\arccos z&{}={\frac {\pi }{2}}-\arcsin z\\&{}={\frac {\pi }{2}}-\left(z+\left({\frac {1}{2}}\right){\frac {z^{3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {z^{5}}{5}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {z^{7}}{7}}+\cdots \right)\\&{}={\frac {\pi }{2}}-\sum _{n=0}^{\infty }\left({\frac {(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {z^{2n+1}}{(2n+1)}};\qquad |z|\leq 1\end{aligned}}}$

${\displaystyle {\begin{aligned}\arctan z&{}=z-{\frac {z^{3}}{3}}+{\frac {z^{5}}{5}}-{\frac {z^{7}}{7}}+\cdots \\&{}=\sum _{n=0}^{\infty }{\frac {(-1)^{n}z^{2n+1}}{2n+1}};\qquad |z|\leq 1\qquad z\neq i,-i\end{aligned}}}$

${\displaystyle {\begin{aligned}\operatorname {arccot} z&{}={\frac {\pi }{2}}-\arctan z\\&{}={\frac {\pi }{2}}-(z-{\frac {z^{3}}{3}}+{\frac {z^{5}}{5}}-{\frac {z^{7}}{7}}+\cdots )\\&{}={\frac {\pi }{2}}-\sum _{n=0}^{\infty }{\frac {(-1)^{n}z^{2n+1}}{2n+1}};\qquad |z|\leq 1\qquad z\neq i,-i\end{aligned}}}$

${\displaystyle {\begin{aligned}\operatorname {arcsec} z&{}=\arccos \left(z^{-1}\right)\\&{}={\frac {\pi }{2}}-\left(z^{-1}+\left({\frac {1}{2}}\right){\frac {z^{-3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {z^{-5}}{5}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {z^{-7}}{7}}+\cdots \right)\\&{}={\frac {\pi }{2}}-\sum _{n=0}^{\infty }\left({\frac {(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {z^{-(2n+1)}}{(2n+1)}};\qquad \left|z\right|\geq 1\end{aligned}}}$

${\displaystyle {\begin{aligned}\operatorname {arccsc} z&{}=\arcsin \left(z^{-1}\right)\\&{}=z^{-1}+\left({\frac {1}{2}}\right){\frac {z^{-3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {z^{-5}}{5}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {z^{-7}}{7}}+\cdots \\&{}=\sum _{n=0}^{\infty }\left({\frac {(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {z^{-(2n+1)}}{2n+1}};\qquad \left|z\right|\geq 1\end{aligned}}}$

Leonhard Euler បានរកឃើញស៊េរីដែលមានភាពប្រសើរជាច្រើនបន្ថែមទៀតសំរាប់អាកតង់សង់ដូចខាងក្រោម៖

${\displaystyle \arctan x={\frac {x}{1+x^{2}}}\sum _{n=0}^{\infty }\prod _{k=1}^{n}{\frac {2kx^{2}}{(2k+1)(1+x^{2})}}.}$

(សំគាល់៖ តួក្នុងផលបូកចំពោះ n= 0 គឺផលគុណទទេ ដែលស្មើ 1)

វាអាចសំដែងដោយ៖

${\displaystyle \arctan x=\sum _{n=0}^{\infty }{\frac {2^{\,2n}\,(n!)^{2}}{\left(2n+1\right)!}}\;{\frac {x^{\,2n+1}}{\left(1+x^{2}\right)^{n+1}}}}$

ប្រភាគបន្តបន្ទាប់ចំពោះអាកតង់សង់

ចំពោះភាពឆ្លាស់នៃស៊េរីស្វ័យគុណសំពោះអាកតង់សង់​គឺវាមានលក្ខណៈជាប្រភាគបន្តបន្ទាប់។

${\displaystyle \arctan(z)={\cfrac {z}{1+{\cfrac {z^{2}}{3+{\cfrac {4z^{2}}{5+{\cfrac {9z^{2}}{7+{\cfrac {16z^{2}}{9+{\cfrac {25z^{2}}{\ddots \,}}}}}}}}}}}}\,}$

វាពិតនីក្នុងបំណែកប្លង់កុំផ្លិច។ មានពីរបំណែកពី −i ដល់ចំនុចដែលមានតំលៃអានន្ត។ និងមួយបំណែកទៀតពី i ដល់ចំនុចត្រង់អានន្ត។ វាដំណើរការឥតខ្ចោះនៅចន្លោះពី −១ ដល់ ១ ។

អាំងតេក្រាលមិនកំនត់នៃអនុគមន៍ត្រីកោណមាត្រច្រាស់

ចំពោះតំលៃពិត និងតំលៃកុំផ្លិចនៃ x

${\displaystyle {\begin{aligned}\int \arcsin x\,dx&{}=x\,\arcsin x+{\sqrt {1-x^{2}}}+C\\\int \arccos x\,dx&{}=x\,\arccos x-{\sqrt {1-x^{2}}}+C\\\int \arctan x\,dx&{}=x\,\arctan x-{\frac {1}{2}}\ln \left(1+x^{2}\right)+C\\\int \operatorname {arccot} x\,dx&{}=x\,\operatorname {arccot} x+{\frac {1}{2}}\ln \left(1+x^{2}\right)+C\\\int \operatorname {arcsec} x\,dx&{}=x\,\operatorname {arcsec} x-\ln \left(x(1+{\sqrt {{x^{2}-1} \over x^{2}}})\right)+C\\\int \operatorname {arccsc} x\,dx&{}=x\,\operatorname {arccsc} x+\ln \left(x(1+{\sqrt {{x^{2}-1} \over x^{2}}})\right)+C\end{aligned}}}$

ចំពោះតំលៃពិតនៃ x≥1៖

${\displaystyle {\begin{aligned}\int \operatorname {arcsec} x\,dx&{}=x\,\operatorname {arcsec} x-\ln \left(x+{\sqrt {x^{2}-1}}\right)+C\\\int \operatorname {arccsc} x\,dx&{}=x\,\operatorname {arccsc} x+\ln \left(x+{\sqrt {x^{2}-1}}\right)+C\end{aligned}}}$

ទាំងអស់នេះអាចទាញបានដោយប្រើអាំងតេក្រាលដោយផ្នែក និងដេរីវេធម្មតា បង្ហាញដូចខាងលើe.

សំរាយបញ្ជាក់ឧទាហរណ៍

ដោយប្រើ ${\displaystyle \int u\,\mathrm {d} v=uv-\int v\,\mathrm {d} u}$ តាង

${\displaystyle {\begin{aligned}u&{}=&\arcsin x&\quad \quad \mathrm {d} v=\mathrm {d} x\\\mathrm {d} u&{}=&{\frac {\mathrm {d} x}{\sqrt {1-x^{2}}}}&\quad \quad {}v=x\end{aligned}}}$

គេបាន

${\displaystyle \int \arcsin x\,\mathrm {d} x=x\arcsin x-\int {\frac {x}{\sqrt {1-x^{2}}}}\,\mathrm {d} x}$

ដោយជំនួស ${\displaystyle k=1-x^{2}\,}$។ នោះ ${\displaystyle \mathrm {d} k=-2x\,\mathrm {d} x}$ និង

${\displaystyle \int {\frac {x}{\sqrt {1-x^{2}}}}\,\mathrm {d} x=-{\frac {1}{2}}\int {\frac {\mathrm {d} k}{\sqrt {k}}}=-{\sqrt {k}}}$

ជំនួសត្រឡប់វិញ x គេបាន

${\displaystyle \int \arcsin x\,\mathrm {d} x=x\arcsin x+{\sqrt {1-x^{2}}}}$

វិធីសាស្រ្តចំបងក្នុងការគណនាអាំងតេក្រាលត្រីកោណមាត្រច្រាស់

• ដើម្បីគណនាអាំងតេក្រាលនៃអាកស៊ីនុស សូមប្រើ៖

${\displaystyle \arcsin x=\arctan {\frac {x}{\sqrt {1-x^{2}}}}}$

• ដើម្បីគណនាអាំងតេក្រាលនៃអាកកូស៊ីនុស សូមប្រើ៖

${\displaystyle \arccos x={\frac {\pi }{2}}-\arcsin x}$

• ដើម្បីគណនាអាំងតេក្រាលនៃអាកតង់សង់ចំពោះ x ក្បែរសូន្យ សូមប្រើវិធីសាស្រ្តគណនាអាកតង់សង់នៃប្រភាគបន្តបន្ទាប់ខាងលើ។ ដើម្បីគណនាអាកតងសង់ចំពោះតំលៃ x ផ្សេងៗទៀត សូមប្រើ៖

${\displaystyle \arctan x=2\arctan {\frac {x}{1+{\sqrt {1+x^{2}}}}}}$

• ដើម្បីគណនាអាកកូតង់សង់ សូមប្រើ៖

${\displaystyle \operatorname {arccot} x={\frac {\pi }{2}}-\arctan x}$

• ដើម្បីគណនាអាកសេកង់ សូមប្រើ៖

${\displaystyle \operatorname {arcsec} x={\frac {\pi }{2}}-\arcsin {\frac {1}{x}}}$

• ដើម្បីគណនាអាកកូសេកង់ សូមប្រើ៖

${\displaystyle \operatorname {arccsc} x=\arcsin {\frac {1}{x}}}$

ទំរង់លោការីត

អនុគមន៍ទាំងនេះអាចសំដែងជាទំរង់លោការីតដោយប្រើ លោការីតកុំផ្លិច។ នេះជាការពន្លាតដែនកំនត់របស់អនុគមន៍ទាំងនេះទៅក្នុងប្លង់កុំផ្លិច។

${\displaystyle {\begin{aligned}\arcsin x&{}=-i\,\log \left(i\,x+{\sqrt {1-x^{2}}}\right)&{}=\operatorname {arccsc} {\frac {1}{x}}\\\arccos x&{}=-i\,\log \left(x+{\sqrt {x^{2}-1}}\right)={\frac {\pi }{2}}\,+i\log \left(i\,x+{\sqrt {1-x^{2}}}\right)={\frac {\pi }{2}}-\arcsin x&{}=\operatorname {arcsec} {\frac {1}{x}}\\\arctan x&{}={\frac {i}{2}}\left(\log \left(1-i\,x\right)-\log \left(1+i\,x\right)\right)&{}=\operatorname {arccot} {\frac {1}{x}}\\\operatorname {arccot} x&{}={\frac {i}{2}}\left(\log \left(1-{\frac {i}{x}}\right)-\log \left(1+{\frac {i}{x}}\right)\right)&{}=\arctan {\frac {1}{x}}\\\operatorname {arcsec} x&{}=-i\,\log \left({\sqrt {{\frac {1}{x^{2}}}-1}}+{\frac {1}{x}}\right)=i\,\log \left({\sqrt {1-{\frac {1}{x^{2}}}}}+{\frac {i}{x}}\right)+{\frac {\pi }{2}}={\frac {\pi }{2}}-\operatorname {arccsc} x&{}=\arccos {\frac {1}{x}}\\\operatorname {arccsc} x&{}=-i\,\log \left({\sqrt {1-{\frac {1}{x^{2}}}}}+{\frac {i}{x}}\right)&{}=\arcsin {\frac {1}{x}}\end{aligned}}}$

សំរាយបញ្ជាក់នៃទំនាក់ទំនងទាំងនេះ​ គឺធ្វើតាមរយៈពន្លាតវាក្នុង​ទំរង់អិចស្ប៉ូណង់ស្យែលនៃ​អនុគមន៍ត្រីកោណមាត្រ។

សំរាយបញ្ជាក់ឧទាហរណ៍

${\displaystyle \arcsin x\,=\,\theta }$

${\displaystyle {\frac {e^{i\,\theta }-e^{-i\,\theta }}{2i}}\,=\,x}$   (និយមន័យអិចស្ប៉ូណង់ស្យែលនៃស៊ីនុស)

តាង

${\displaystyle k=e^{i\,\theta }.}$

គេបាន

${\displaystyle {\frac {k-{\frac {1}{k}}}{2i}}\,=\,x}$

${\displaystyle k^{2}-2\,i\,k\,x-1\,=\,0}$   (ដំណោះស្រាយចំពោះ${\displaystyle k}$)

${\displaystyle k\,=\,i\,x\pm {\sqrt {1-x^{2}}}\,=\,e^{i\,\theta }}$   (យកផ្នែកខាងវិជ្ជមាន)

${\displaystyle \theta \,=\,\arcsin \,x\,=\,-i\log \left(i\,x+{\sqrt {1-x^{2}}}\right)}$  Q.E.D.

អនុគមន៍ត្រីកោណមាត្រច្រាស់ក្នុងប្លង់កុំផ្លិច'

${\displaystyle \arcsin(z)\,}$	${\displaystyle \arccos(z)\,}$	${\displaystyle \arctan(z)\,}$	${\displaystyle \operatorname {arccot}(z)\,}$	${\displaystyle \operatorname {arcsec}(z)\,}$	${\displaystyle \operatorname {arccsc}(z)\,}$

រូបមន្តអាកតង់សង់បន្ថែម

${\displaystyle \color {blue}\arctan u+\arctan v=\arctan \left({\frac {u+v}{1-uv}}\right)}$

សំរាយបញ្ជាក់

ចាប់ផ្តើមពី

${\displaystyle \tan(\alpha +\beta )={\frac {\tan \alpha +\tan \beta }{1-\tan \alpha \tan \beta }}\,}$

និងតាង

${\displaystyle u\,=\,\tan \,\alpha \,,\,v=\,\tan \,\beta }$

បំរើបំរាស់ក្នុងការអនុវត្តន៍

ត្រីកោណកែង

អនុគមន៍ត្រីកោណមាត្រ​មានសារៈសំខាន់នៅពេលគេចង់រករ​ង្វាស់មុំដែលនៅសល់ពីរផ្សេងទៀតនៃត្រីកោណកែង ដែលគេស្គាល់រួចជាស្រេចនូវ​រង្វាស់ប្រវែងនៃត្រីកោណកែងនេះ។ ដោយប្រើអនុគមន៍ត្រីកោណមាត្រច្រាស់

${\displaystyle \theta =\arcsin \left({\frac {\text{opposite}}{\text{hypotenuse}}}\right)}$

សំគាល់៖ opposite = ជ្រុងឈម, hypotenuse = អ៊ីប៉ូតេនុស និង adjacent = ជ្រុងជាប់

ជាញឹកញាប់ អ៊ីប៉ូតេនុសជារង្វាស់ជ្រុងដែលគេមិនប្រាប់ និងចាំបាច់ត្រូវរកមុនពេលប្រើប្រាស់អាក់ស៊ីនុស ឬ អាកកូស៊ីនុស។ អ្នកអាចគណនាមុំនៃត្រីកោណដោយមិនចាំបាច់ដឹងប្រវែងអ៊ីប៉ូតេនុសក៏បាន។

${\displaystyle \theta =\arctan \left({\frac {\text{opposite}}{\text{adjacent}}}\right)}$