포물면

기하학에서 포물면(Paraboloid)은 정확히 하나의 대칭축을 가지며 대칭 중심이 없는 이차 곡면이다. "포물면"이라는 용어는 유사한 대칭 속성을 갖는 원뿔 곡선인 포물선에서 유래했다.

회전 포물면

대칭축에 평행한 평면으로 포물면을 자른 모든 평면 단면은 포물선이다. 다른 모든 평면 단면이 쌍곡선, 또는 두 개의 교차하는 선(접평면으로 자른 경우)이면 포물면은 쌍곡 포물면이다. 다른 모든 비어있지 않은 평면 단면이 타원, 또는 하나의 점(접평면으로 자른 경우)이면 포물면은 타원 포물면이다. 포물면은 타원형이거나 쌍곡형이다.

동등하게, 포물면은 원기둥이 아니고 복소수 위에서 이차 항의 부분이 두 개의 서로 다른 선형 인수로 인수분해될 수 있는 음함수 방정식을 갖는 이차 곡면으로 정의될 수 있다. 인수가 실수이면 포물면은 쌍곡형이고, 인수가 켤레 복소수이면 타원형이다.

타원 포물면은 타원형 컵 모양을 가지며 축이 수직일 때 최대값 또는 최소값을 갖는다. 세 축 x, y, z를 갖는 적절한 좌표계에서 다음 방정식으로 표현될 수 있다.^[1] $${\displaystyle z={\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}.}$$ 여기서 a와 b는 각각 xz 및 yz 평면에서 곡률의 정도를 결정하는 상수이다. 이 위치에서 타원 포물면은 위로 열린다.

쌍곡 포물면

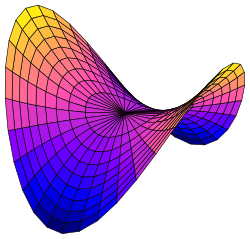
쌍곡 포물면은 (쌍곡면과 혼동하지 말 것) 안장 모양의 이중 곡면이다. 적절한 좌표계에서 쌍곡 포물면은 다음 방정식으로 표현될 수 있다.^[2][3] $${\displaystyle z={\frac {y^{2}}{b^{2}}}-{\frac {x^{2}}{a^{2}}}.}$$ 이 위치에서 쌍곡 포물면은 x-축을 따라 아래로 열리고 y-축을 따라 위로 열린다 (즉, 평면 x = 0의 포물선은 위로 열리고 평면 y = 0의 포물선은 아래로 열린다).

모든 포물면(타원형 또는 쌍곡형)은 두 번째 포물선에 의해 유도되는 움직이는 포물선에 의해 생성될 수 있으므로 평행 이동 곡면이다.

속성 및 응용

타원 포물면

원형 포물면의 폴리곤 메시

원형 포물면

적절한 데카르트 좌표계에서 타원 포물면은 다음 방정식을 갖는다. $${\displaystyle z={\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}.}$$

만약 a = b이면, 타원 포물면은 원형 포물면 또는 회전 포물면이다. 이것은 포물선을 그 축을 중심으로 회전시켜 얻은 회전면이다.

원형 포물면은 원을 포함한다. 이것은 일반적인 경우에도 마찬가지이다 (원호형 단면 문서 참고).

사영기하학의 관점에서, 타원 포물면은 무한원 평면에 접하는 타원면이다.

평면 단면

타원 포물면의 평면 단면은 다음과 같다.

• 평면이 축에 평행하면 포물선,
• 평면이 접평면이면 한 점,
• 그렇지 않으면 타원이거나 비어있음.

포물선 반사경

 이 부분의 본문은 포물선 반사경 및 파라볼라 안테나입니다.

원형 포물면의 축에는 초점 (또는 초점)이라고 불리는 점이 있는데, 만약 포물면이 거울이라면 초점의 점 광원에서 나오는 빛(또는 다른 파동)은 포물면의 축에 평행한 평행 빔으로 반사된다. 이것은 반대로도 작동한다: 포물면의 축에 평행한 평행 빔은 초점에 집중된다.

따라서 원형 포물면의 모양은 천문학에서 포물선 반사경과 파라볼라 안테나에 널리 사용된다.

회전하는 액체의 표면도 원형 포물면이다. 이것은 액체 거울 망원경과 고체 망원경 거울 제작 (회전로 참조)에 사용된다.

• 
  원형 포물면 거울로 들어오는 평행 광선은 초점 F로 반사되거나 그 반대이다.
• 
  포물선 반사경
• 
  유리잔 속의 회전하는 물

쌍곡 포물면

선이 포함된 쌍곡 포물면

프링글스 튀김 과자는 쌍곡 포물면 모양이다.

쌍곡 포물면은 이중 곡면: 서로 꼬인 위치에 있는 두 가지 선군을 포함한다. 각 선군의 선들은 공통 평면에 평행하지만 서로는 평행하지 않다. 따라서 쌍곡 포물면은 코노이드(conoid)이다.

이러한 속성들은 쌍곡 포물면을 특징지으며 쌍곡 포물면의 가장 오래된 정의 중 하나에 사용된다: 쌍곡 포물면은 고정된 평면에 평행하고 두 개의 고정된 꼬인 선을 가로지르는 움직이는 선에 의해 생성될 수 있는 곡면이다.

이러한 속성 덕분에 콘크리트 지붕부터 스낵 식품에 이르기까지 다양한 재료와 다양한 용도로 쌍곡 포물면을 쉽게 제작할 수 있다. 특히 프링글스 튀김 과자는 잘린 쌍곡 포물면과 유사하다.^[4]

쌍곡 포물면은 모든 점에서 가우스 곡률이 음수이므로 안장 곡면이다. 따라서 곡면임에도 불구하고 전개 가능하지 않다.

사영기하학의 관점에서, 쌍곡 포물면은 무한원 평면에 접하는 한 겹 쌍곡면이다.

방정식 ${\displaystyle z=axy}$ 또는 ${\displaystyle z={\tfrac {a}{2}}(x^{2}-y^{2})}$인 쌍곡 포물면은 (좌표축 회전까지) 직각 쌍곡선과 유사하게 직각 쌍곡 포물면이라고 불릴 수 있다.

평면 단면

방정식이 $${\displaystyle z={\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}}$$ 인 쌍곡 포물면의 평면 단면은 다음과 같다.

• 평면이 z-축에 평행하고 ${\displaystyle bx\pm ay+b=0}$ 형태의 방정식을 가지면 직선,
• 평면이 z-축에 평행하고 단면이 직선이 아니면 포물선,
• 평면이 접평면이면 교차하는 한 쌍의 직선,
• 그렇지 않으면 쌍곡선.

STL 쌍곡 포물면 모델

건축에서의 예시

안장 지붕은 재료의 직선 부분으로 쉽게 지을 수 있기 때문에 종종 쌍곡 포물면으로 만들어진다. 몇 가지 예는 다음과 같다.

• 필립스 파빌리온 엑스포 '58, 브뤼셀 (1958)
• 인도 공과대학교 델리 - 도그라 홀 지붕
• 가톨릭 세키구치 교회, 일본 도쿄 (1964)
• 세인트 리처드 교회, 햄, 잉글랜드 런던 햄 (1966)
• 샌프란시스코 성모마리아 대성당, 미국 캘리포니아 샌프란시스코 (1971)
• 새들돔, 캐나다 앨버타 캘거리 (1983)
• 스칸디나비움, 스웨덴 예테보리 (1971)
• 오세아노그라픽, 스페인 발렌시아 (2003)
• 런던 벨로파크, 잉글랜드 (2011)
• 워터월드 레저 및 활동 센터, 렉섬, 웨일스 (1970)
• 마크햄 무어 서비스 스테이션 지붕, A1(남향), 노팅엄셔, 잉글랜드
• 카페 "코메타", 러시아 모스크바 소콜 지구 (1960). 건축가 V. 볼로딘, 엔지니어 N. 드로즈도프. 철거됨.

• 
  쌍곡 포물면 구조의 예인 바르샤바 오호타 철도역
• 
  쌍곡 포물면을 설명하는 표면
• 
  멕시코 소치밀코 로스 마난티알레스 레스토랑
• 
  스페인 발렌시아 오세아노그라픽의 쌍곡 포물면 얇은 껍질 지붕 (2019년 촬영)
• 
  노팅엄셔 마크햄 무어 서비스 스테이션 지붕 (2009년 사진)

타원 포물면과 쌍곡 포물면의 다발 사이의 원기둥

타원 포물면, 포물선 원기둥, 쌍곡 포물면

타원 포물면의 다발 $${\displaystyle z=x^{2}+{\frac {y^{2}}{b^{2}}},\ b>0,}$$ 과 쌍곡 포물면의 다발 $${\displaystyle z=x^{2}-{\frac {y^{2}}{b^{2}}},\ b>0,}$$ 은 ${\displaystyle b\rightarrow \infty }$일 때 동일한 곡면 $${\displaystyle z=x^{2}}$$ 에 접근하는데, 이것은 포물선 원기둥이다 (그림 참조).

곡률

간단히 다음과 같이 매개변수화된 타원 포물면은 $${\displaystyle {\vec {\sigma }}(u,v)=\left(u,v,{\frac {u^{2}}{a^{2}}}+{\frac {v^{2}}{b^{2}}}\right)}$$ 가우스 곡률 $${\displaystyle K(u,v)={\frac {4}{a^{2}b^{2}\left(1+{\frac {4u^{2}}{a^{4}}}+{\frac {4v^{2}}{b^{4}}}\right)^{2}}}}$$ 과 평균곡률 $${\displaystyle H(u,v)={\frac {a^{2}+b^{2}+{\frac {4u^{2}}{a^{2}}}+{\frac {4v^{2}}{b^{2}}}}{a^{2}b^{2}{\sqrt {\left(1+{\frac {4u^{2}}{a^{4}}}+{\frac {4v^{2}}{b^{4}}}\right)^{3}}}}}}$$ 을 가지는데, 이 둘은 항상 양수이며 원점에서 최댓값을 갖고, 표면 위의 점이 원점에서 멀어질수록 작아지며, 해당 점이 원점에서 무한히 멀어질수록 점근적으로 0에 수렴한다.

쌍곡 포물면^[2]은 다음과 같이 매개변수화될 때 $${\displaystyle {\vec {\sigma }}(u,v)=\left(u,v,{\frac {u^{2}}{a^{2}}}-{\frac {v^{2}}{b^{2}}}\right)}$$ 가우스 곡률 $${\displaystyle K(u,v)={\frac {-4}{a^{2}b^{2}\left(1+{\frac {4u^{2}}{a^{4}}}+{\frac {4v^{2}}{b^{4}}}\right)^{2}}}}$$ 과 평균곡률 $${\displaystyle H(u,v)={\frac {-a^{2}+b^{2}-{\frac {4u^{2}}{a^{2}}}+{\frac {4v^{2}}{b^{2}}}}{a^{2}b^{2}{\sqrt {\left(1+{\frac {4u^{2}}{a^{4}}}+{\frac {4v^{2}}{b^{4}}}\right)^{3}}}}}.}$$ 을 갖는다.

구구단의 기하학적 표현

만약 쌍곡 포물면 $${\displaystyle z={\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}}$$ 이 +z 방향으로 ( 오른손 법칙에 따라) ⁠π/4⁠ 각도로 회전하면 그 결과는 다음 곡면이 된다. $${\displaystyle z=\left({\frac {x^{2}+y^{2}}{2}}\right)\left({\frac {1}{a^{2}}}-{\frac {1}{b^{2}}}\right)+xy\left({\frac {1}{a^{2}}}+{\frac {1}{b^{2}}}\right)}$$ 그리고 만약 a = b이면 이것은 다음으로 단순화된다. $${\displaystyle z={\frac {2xy}{a^{2}}}.}$$ 마지막으로, a = √2라고 하면, 쌍곡 포물면 $${\displaystyle z={\frac {x^{2}-y^{2}}{2}}.}$$ 이 곡면 $${\displaystyle z=xy}$$ 와 합동임을 알 수 있는데, 이는 구구단의 기하학적 표현 (말하자면 3차원 노모그램)으로 생각할 수 있다.

두 포물면 R² → R 함수 $${\displaystyle z_{1}(x,y)={\frac {x^{2}-y^{2}}{2}}}$$ 와 $${\displaystyle z_{2}(x,y)=xy}$$ 는 조화 켤레 함수이며, 함께 해석 함수 $${\displaystyle f(z)={\frac {z^{2}}{2}}=f(x+yi)=z_{1}(x,y)+iz_{2}(x,y)}$$ 를 형성하는데, 이는 R → R 포물선 함수 f(x) = ⁠x²/2⁠의 해석적 연속이다.

포물면 접시의 치수

대칭 포물면 접시의 치수는 다음 방정식으로 관련된다. $${\displaystyle 4FD=R^{2},}$$ 여기서 F는 초점 거리, D는 접시의 깊이 (정점부터 테두리 평면까지 대칭축을 따라 측정), R은 테두리의 반경이다. 이들은 모두 동일한 길이 단위여야 한다. 이 세 길이 중 두 개를 알면 이 방정식을 사용하여 세 번째를 계산할 수 있다.

접시의 표면을 따라 측정한 지름을 찾으려면 더 복잡한 계산이 필요하다. 이것은 때때로 "선형 지름"이라고 불리며, 접시를 만들기 위해 자르고 구부리기에 적절한 크기의 평평하고 원형인 재료 시트 (일반적으로 금속)의 지름과 같다. 계산에 유용한 두 가지 중간 결과는 다음과 같다. P = 2F (또는 동등하게: P = ⁠R²/2D⁠) 및 Q = √P² + R²)이며, 여기서 F, D, R은 위에서 정의된 바와 같다. 표면을 따라 측정한 접시의 지름은 다음으로 주어진다. $${\displaystyle {\frac {RQ}{P}}+P\ln \left({\frac {R+Q}{P}}\right),}$$ 여기서 ln x는 x의 자연로그, 즉 e를 밑으로 하는 로그를 의미한다.

접시의 부피, 즉 테두리가 수평이고 정점이 바닥에 있을 때 담을 수 있는 액체의 양 (예: 포물면 웍의 용량)은 다음으로 주어진다. $${\displaystyle {\frac {\pi }{2}}R^{2}D,}$$ 여기서 기호는 위에서 정의된 바와 같다. 이것은 원기둥 (πR²D), 반구 (⁠2π/3⁠R²D, 여기서 D = R), 그리고 원뿔 (⁠π/3⁠R²D})의 부피 공식과 비교할 수 있다. πR²는 접시의 개구면적, 즉 테두리에 의해 둘러싸인 영역으로, 반사경 접시가 가로챌 수 있는 햇빛의 양에 비례한다. 포물면 접시의 표면적은 회전면의 면적 공식을 사용하여 찾을 수 있으며 다음과 같다. $${\displaystyle A={\frac {\pi R\left({\sqrt {(R^{2}+4D^{2})^{3}}}-R^{3}\right)}{6D^{2}}}.}$$

같이 보기

• 타원면
• 쌍곡면
• 포물선 반사경