Czynnik pierwszy

Czynnik pierwszy – dowolna liczba pierwsza, która dzieli bez reszty daną liczbę naturalną^[1]. Na przykład jednym z czynników pierwszych liczby 20 jest 5.

Diagram Hassego przedstawiający rozkład na czynniki liczby 42

Inny diagram Hassego przedstawiający rozkład liczby 42 na czynniki – zaczyna się inaczej, ale kończy się jednakowymi czynnikami pierwszymi: 2,3,7

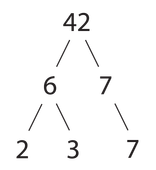
Jedna z podstawowych obserwacji dotyczących liczb naturalnych mówi: każda liczba naturalna większa od 1 jest albo pierwsza, albo ma przynajmniej jeden czynnik pierwszy. Z niej wynika kolejna: każda liczba naturalna większa od 1 jest pierwsza lub daje się zapisać w postaci iloczynu liczb pierwszych. Twierdzenie to nazywa się podstawowym twierdzeniem arytmetyki.

Przedstawienie danej liczby złożonej w postaci iloczynu czynników pierwszych nazywa się rozkładem liczby na czynniki pierwsze. Rozkład ten jest jednoznaczny w tym sensie, że wszystkie rozkłady danej liczby na czynniki pierwsze różnią się tylko ich kolejnością.

Na przykład: ${\displaystyle 20=2\cdot 2\cdot 5=5\cdot 2\cdot 2=2\cdot 5\cdot 2=2^{2}\cdot 5.}$

Dla czynników pierwszych prawdziwe są m.in. poniższe stwierdzenia:

• każda liczba złożona ma czynnik pierwszy, który nie przekracza pierwiastka kwadratowego z tej liczby;
• każda liczba naturalna postaci 4k + 3 jest albo pierwsza, albo ma przynajmniej jeden czynnik pierwszy tej postaci
  • ${\displaystyle 63=4\cdot 15+3}$ i ${\displaystyle 63=9\cdot 7,}$ przy czym ${\displaystyle 7=4\cdot 1+3;}$
• każda liczba naturalna postaci 6k + 5 jest albo pierwsza, albo ma przynajmniej jeden czynnik pierwszy tej postaci
  • ${\displaystyle 119=6\cdot 19+5}$ i ${\displaystyle 119=7\cdot 17,}$ przy czym ${\displaystyle 17=6\cdot 2+5.}$

Rozkład liczby naturalnej na czynniki pierwsze ma wysoką złożoność obliczeniową, co stanowi podstawę algorytmów stosowanych w kryptografii asymetrycznej (patrz np. klucz RSA).

Rozkład liczby wymiernej na czynniki

Osobny artykuł: Rozkład na czynniki.

Rozkład na czynniki pierwsze (inaczej faktoryzacja z angielskiego factorization) można też jednoznacznie wykonać dla dowolnej dodatniej liczby wymiernej ${\displaystyle r.}$ Wówczas:

${\displaystyle r=2^{w_{2}}\cdot 3^{w_{3}}\cdot 5^{w_{5}}\cdot 7^{w_{7}}\cdot \ldots ,}$
gdzie ${\displaystyle w_{p}}$ są liczbami całkowitymi.

Taki rozkład ma duże znaczenie w teorii liczb, w szczególności służy do konstrukcji liczb p-adycznych.

Algorytm rozkładu na czynniki pierwsze

Elementarnym sposobem rozkładu liczb na czynniki pierwsze jest wykonywanie kolejnych dzieleń, np.:

56|2 28|2 14|2 7|7 1|

Szukamy najmniejszej liczby pierwszej dzielącej daną liczbę (56). Jest to 2. Dzielimy: 56/2=28. Powtarzamy tę czynność dla kolejnych wyników aż do uzyskania w ilorazie liczby 1. Otrzymujemy wówczas wszystkie dzielniki pierwsze szukanej liczby. Na schemacie znajdują się one po prawej stronie.

Zobacz też

Zobacz w Wikiźródłach tekst Tablica liczb pierwszych i rozkładów na czynniki pierwsze

• ideał pierwszy