Дробно-линейная функция

Эта статья о дробно-линейной функции; о дробно-линейном преобразовании см. Дробно-линейное преобразование.

Дро́бно-лине́йная фу́нкция — это числовая функция, которая может быть представлена в виде дроби, числителем и знаменателем которой являются линейные функции.

Равнобочная гипербола — простейший пример дробно-линейной функции

Дробно-линейная функция, отображающая в общем случае ${\displaystyle n}$-мерное числовое пространство в одномерное числовое, представляет собой важный частный случай:

• при ${\displaystyle n=1}$ как в вещественном, так и комплексном пространстве — рациональной функции, отображающей в общем случае одномерное числовое пространство само в себя с помощью многочленов одной переменной произвольной степени;
• при ${\displaystyle n=1}$ в комплексном пространстве — дробно-линейного преобразования, отображающего в общем случае многомерное комплексное пространство само в себя;
• при ${\displaystyle n=1}$ в комплексном и при ${\displaystyle n=2}$ в вещественном пространстве, инвертируя относительно окружностей, — частный случай преобразования Мёбиуса.

Формальное определение

Дробно-линейная функция — это числовая функция вида

${\displaystyle \mathbb {U} ^{n}\to \mathbb {U} :w=L(u_{1},u_{2},\dots ,u_{n})={\frac {a_{1}u_{1}+a_{2}u_{2}+\cdots +a_{n}u_{n}+b}{c_{1}u_{1}+c_{2}u_{2}+\cdots +c_{n}u_{n}+d}},}$

где ${\displaystyle \mathbb {U} }$ — комплексные (${\displaystyle \mathbb {Z} }$) или вещественные (${\displaystyle \mathbb {R} }$) числа, ${\displaystyle u_{1},u_{2},\dots ,u_{n}}$ — соответственно комплексные или вещественные переменные, ${\displaystyle a_{1},a_{2},\dots ,a_{n},}$ ${\displaystyle c_{1},c_{2},\dots ,c_{n},}$ ${\displaystyle b,d}$ — соответственно комплексные или вещественные коэффициенты,

${\displaystyle |c_{1}|+|c_{2}|+\dots +|c_{n}|+|d|>0}$^[1].

Возможно обобщение на кватернионы^[2].

Вырожденные случаи^[1]:

• если

${\displaystyle |c_{1}|=|c_{2}|=\dots =|c_{n}|=0,}$

то дробно-линейная функция становится целой линейной функций;

• если ранг матрицы

${\displaystyle \left({\begin{array}{cccc}a_{1}&a_{2}&\ldots &a_{n}&b\\c_{1}&c_{2}&\ldots &c_{n}&d\end{array}}\right)}$

равен единице, то дробно-линейная функция вырождается в постоянную.

У собственно (невырожденной) дробно-линейной функции^[1]:

• ${\displaystyle |c_{1}|+|c_{2}|+\dots +|c_{n}|>0;}$
• равен двум ранг матрицы

${\displaystyle \left({\begin{array}{cccc}a_{1}&a_{2}&\ldots &a_{n}&b\\c_{1}&c_{2}&\ldots &c_{n}&d\end{array}}\right).}$

Вещественная дробно-линейная функция

Вещественная дробно-линейная функция — это числовая функция вида

${\displaystyle \mathbb {R} ^{n}\to \mathbb {R} :y=L(x_{1},x_{2},\dots ,x_{n})={\frac {a_{1}x_{1}+a_{2}x_{2}+\cdots +a_{n}x_{n}+b}{c_{1}x_{1}+c_{2}x_{2}+\cdots +c_{n}x_{n}+d}},}$

где ${\displaystyle \mathbb {R} }$ — вещественные числа, ${\displaystyle x_{1},x_{2},\dots ,x_{n}}$ — вещественные переменные, ${\displaystyle a_{1},a_{2},\dots ,a_{n},}$ ${\displaystyle c_{1},c_{2},\dots ,c_{n},}$ ${\displaystyle b,d}$ — вещественные коэффициенты,

${\displaystyle |c_{1}|+|c_{2}|+\dots +|c_{n}|+|d|>0}$^[1].

Функция одной переменной

Равнобочная гипербола как вещественная дробно-линейная функция ${\displaystyle {\frac {2x-1}{x+2}}}$ с асимптотами ${\displaystyle x=-2/1=-2}$ и ${\displaystyle y=2/1=2}$, ${\displaystyle ad-bc=5>0}$

В простейшем случае ${\displaystyle n=1}$ и действительных

${\displaystyle x_{1}=x,}$ ${\displaystyle a_{1}=a,}$ ${\displaystyle b,}$ ${\displaystyle c_{1}=c,}$ ${\displaystyle d}$

график дробно-линейной функции

${\displaystyle y={\frac {ax+b}{cx+d}}}$ —

равнобочная гипербола с асимптотами

${\displaystyle x=-d/c}$

и

${\displaystyle y=a/c,}$

параллельными осям координат^[1].

Асимптоты гиперболы

Пусть дробно-линейная функция одного переменного

${\displaystyle y={\frac {ax+b}{cx+d}}}$

несократима, то есть ${\displaystyle ad-bc\neq 0}$, и не сводится к целой линейной функции, то есть ${\displaystyle c\neq 0}$. Выделим целую часть дроби и вынесем за скобки коэффициент при ${\displaystyle x}$^[3]:

${\displaystyle y={\frac {\displaystyle {\frac {a}{c}}x+{\frac {b}{c}}}{\displaystyle x+{\frac {d}{c}}}}={\frac {\displaystyle {\frac {a}{c}}\left(x+{\frac {d}{c}}\right)+\left({\frac {b}{c}}-{\frac {ad}{c^{2}}}\right)}{\displaystyle x+{\frac {d}{c}}}}=}$

${\displaystyle ={\frac {a}{c}}-{\frac {ad-bc}{c^{2}\left(\displaystyle x+{\frac {d}{c}}\right)}}.}$

Теперь ясно, что график функции ${\displaystyle {\frac {ax+b}{cx+d}}}$ получается из графика ${\displaystyle {\frac {1}{x}}}$ следующими элементарными преобразованиями:

• растяжением в ${\displaystyle \left|{\frac {ad-bc}{c^{2}}}\right|}$ раз по оси ${\displaystyle Oy}$, причём в случае ${\displaystyle ad-bc>0}$ с отражением относительно оси ${\displaystyle Ox}$;
• перенесением параллельно оси ${\displaystyle Ox}$ на ${\displaystyle -{\frac {d}{c}}}$;
• перенесением параллельно оси ${\displaystyle Oy}$ на ${\displaystyle {\frac {a}{c}}}$.

Таким образом, дробно-линейная функция одного переменного ${\displaystyle {\frac {ax+b}{cx+d}}}$ — это обыкновенная гипербола второго порядка, прямые ${\displaystyle x=-{\frac {d}{c}}}$ и ${\displaystyle y={\frac {a}{c}}}$ — асимптоты гиперболы, взаимно перпендикулярные и параллельные осям координат, а точка пересечения асимптот ${\displaystyle \left(-{\frac {d}{c}},{\frac {a}{c}}\right),}$ не принадлежащая кривой, — её центр^[3].

Также очевидно, что дробно-линейная функция одного переменного ${\displaystyle {\frac {ax+b}{cx+d}}}$^[3]:

• «теряет смысл», то есть не имеет никакого значения, перестаёт «существовать» в точке ${\displaystyle x=-{\frac {d}{c}}}$;
• на интервалах ${\displaystyle \left(-\infty ,-{\frac {d}{c}}\right)}$ и ${\displaystyle \left(-{\frac {d}{c}},+\infty \right)}$ функция везде возрастает при ${\displaystyle ad-bc>0}$ и везде убывает при ${\displaystyle ad-bc<0}$;
• при неограниченном увеличении ${\displaystyle |x|}$ значения функции неограниченно приближаются к ${\displaystyle {\frac {a}{c}}}$, что видно также из преобразования

${\displaystyle {\frac {ax+b}{cx+d}}={\frac {\displaystyle a+{\frac {b}{x}}}{\displaystyle c+{\frac {d}{x}}}}.}$

Производная^[4]:

${\displaystyle {\Biggl (}{\frac {a}{c}}-{\frac {ad-bc}{c^{2}\left(\displaystyle x+{\frac {d}{c}}\right)}}{\Biggr )}'={\frac {ad-bc}{c^{2}\left(\displaystyle x+{\frac {d}{c}}\right)^{2}}}.}$

Неопределённый интеграл:

${\displaystyle \int {\Biggl (}{\frac {a}{c}}-{\frac {ad-bc}{c^{2}\left(\displaystyle x+{\frac {d}{c}}\right)}}{\Biggr )}dx={\frac {a}{c}}x-{\frac {ad-bc}{c^{2}}}\ln \left|x+{\frac {d}{c}}\right|+C.}$

Каноническое уравнение гиперболы

Сначала приведём функцию

${\displaystyle y={\frac {a}{c}}-{\frac {ad-bc}{\displaystyle c^{2}\left(x+{\frac {d}{c}}\right)}}}$

преобразованиями координат

${\displaystyle x'=x+{\frac {d}{c}},}$ ${\displaystyle y'=y-{\frac {a}{c}},}$ ${\displaystyle m=-{\frac {ad-bc}{c^{2}}}}$

к простейшему виду

${\displaystyle y'={\frac {m}{x'}}}$,

который называется уравнением обратной пропорциональности величин ${\displaystyle x'}$ и ${\displaystyle y'}$^[5].

Теперь повернём координатные оси на угол ${\displaystyle 45^{\circ },}$ сделав замену координат

${\displaystyle x'=x''\cos(45^{\circ })-y''\sin(45^{\circ })={\frac {x''-y''}{\sqrt {2}}},}$

${\displaystyle y'=x''\sin(45^{\circ })+y''\cos(45^{\circ })={\frac {x''+y''}{\sqrt {2}}},}$

получим в новых координатах^[5]:

${\displaystyle x'y'=m,}$ ${\displaystyle {\frac {x''-y''}{\sqrt {2}}}{\frac {x''+y''}{\sqrt {2}}}=m,}$

${\displaystyle {\frac {x''^{2}}{2m}}-{\frac {y''^{2}}{2m}}=1.}$

Последнее уравнение есть каноническое уравнение равносторонней гиперболы с полуосями ${\displaystyle a=b={\sqrt {2|m|}}.}$^[5]

Функция двух переменных

Гиперболический параболоид

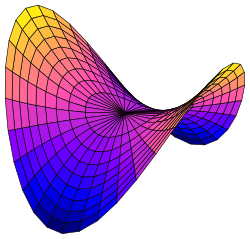
В случае ${\displaystyle n=2}$ и действительных ${\displaystyle x_{1},}$ ${\displaystyle x_{2},}$ ${\displaystyle a_{1},}$ ${\displaystyle a_{2},}$ ${\displaystyle b,}$ ${\displaystyle c_{1},}$ ${\displaystyle c_{2},}$ ${\displaystyle d}$ график дробно-линейной функции

${\displaystyle y={\frac {a_{1}x_{1}+a_{2}x_{2}+b}{c_{1}x_{1}+c_{2}x_{2}+d}}}$

представляет собой гиперболический параболоид^[1].

Комплексная дробно-линейная функция

Основная статья: Дробно-линейное преобразование

Комплексная дробно-линейная функция — числовая функция вида

${\displaystyle \mathbb {C} ^{n}\to \mathbb {C} :w=L(z_{1},z_{2},\dots ,z_{n})={\frac {a_{1}z_{1}+a_{2}z_{2}+\cdots +a_{n}z_{n}+b}{c_{1}z_{1}+c_{2}z_{2}+\cdots +c_{n}z_{n}+d}},}$

где ${\displaystyle \mathbb {C} }$ — комплексные числа, ${\displaystyle z_{1},z_{2},\dots ,z_{n}}$ — комплексные переменные, ${\displaystyle a_{1},a_{2},\dots ,a_{n},}$ ${\displaystyle c_{1},c_{2},\dots ,c_{n},}$ ${\displaystyle b,d}$ — комплексные коэффициенты,

${\displaystyle |c_{1}|+|c_{2}|+\dots +|c_{n}|+|d|>0}$^[1].

Основная статья: Дробно-линейное преобразование комплексной плоскости

При ${\displaystyle n=1}$ комплексная дробно-линейная функция

${\displaystyle \mathbb {C} \to \mathbb {C} :w=L(z)={\frac {az+b}{cz+d}}}$ —

аналитическая функция одной комплексной переменной всюду в расширенной комплексной плоскости ${\displaystyle {\widehat {\mathbb {C} }}=\mathbb {C} \cup \{\infty \}}$, за исключением точки ${\displaystyle z=-d/c}$, в которой комплексная дробно-линейная функция имеет простой полюс^[1].

При ${\displaystyle n\geqslant 1}$ комплексная дробно-линейная функция

${\displaystyle \mathbb {C} ^{n}\to \mathbb {C} :w=L(z_{1},z_{2},\dots ,z_{n})={\frac {a_{1}z_{1}+a_{2}z_{2}+\cdots +a_{n}z_{n}+b}{c_{1}z_{1}+c_{2}z_{2}+\cdots +c_{n}z_{n}+d}},}$ —

мероморфная функция в пространстве ${\displaystyle \mathbb {C} ^{n}}$ комплексных переменных ${\displaystyle z_{1},z_{2},\dots ,z_{n}}$, имеющая полярное множество

${\displaystyle \{z\in \mathbb {C} ^{n};c_{1}z_{1}+c_{2}z_{2}+\cdots +c_{n}z_{n}+d=0\}}$^[1].