Математическая константа

Термин «Константа» имеет также другие значения.

Математическая константа или математическая постоянная — величина, значение которой не меняется; в этом она противоположна переменной. В отличие от физических постоянных, математические постоянные определены независимо от каких бы то ни было физических измерений.

Длина окружности с диаметром ${\displaystyle 1}$ равна ${\displaystyle \pi }$

Некоторые избранные постоянные

Использованные сокращения: И — иррациональное число, А — алгебраическое число, Т — трансцендентное число, ? — неизвестно; мат — обычная математика, ТЧ — теория чисел, ТХ — теория хаоса, комб — комбинаторика, АИТ — алгоритмическая теория информации.

Символ	Приближенное значение	Название	Область	Значение	Впервые описана	Число известных знаков
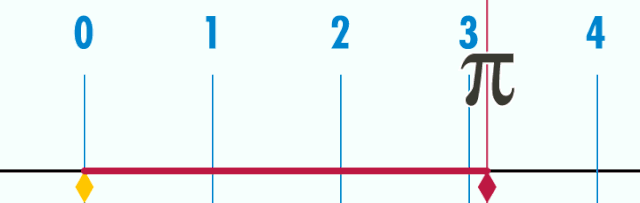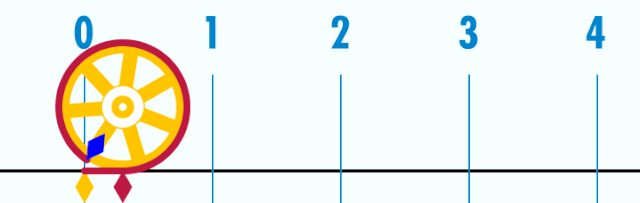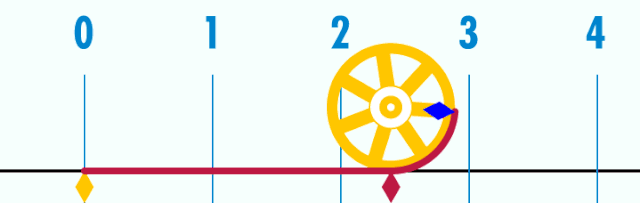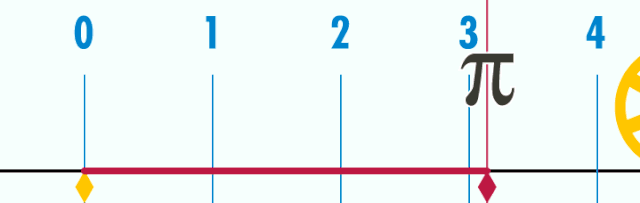
${\displaystyle \pi }$	≈ 3,141 592 653 589 793 238 462 643 383 279 502 88	пи, архимедова константа	мат	Т, И	до 2600 до н. э. (Месопотамия, Египет)	100 000 000 000 000[1][2]
${\displaystyle \tau }$	≈ 6,283 185 307 179 586	тау (2π)	мат	Т, И	2001	100 000 000 000 000
e	≈ 2,718 281 828 459 045 235 360 287 471 352 662 50	константа Непера, число Эйлера, основание натурального логарифма	мат	Т, И	1618	8 000 000 000 000
${\displaystyle {\sqrt {2}}}$	≈ 1,414 213 562 373 095 048 801 688 724 209 698 08	константа Пифагора, квадратный корень из 2	мат	А, И	до 1800 до н. э.	10 000 000 000 000
${\displaystyle {\sqrt {3}}}$	≈ 1,732 050 807 568 877 293 527 446 341 505 872 37	константа Феодора, квадратный корень из 3	мат	А, И	до 800 до н. э.	2 000 000 000 000
γ	≈ 0,577 215 664 901 532 860 606 512 090 082 402 43	постоянная Эйлера — Маскерони	мат, ТЧ	?	1735	108 000 000
φ	≈ 1,618 033 988 749 894 848 204 586 834 365 638 12	золотое сечение	мат	А, И	ок. 300 до н. э.	3 141 000 000
β*	≈ 0,702 58	константа Эмбри — Трефетена	ТЧ	?
δ	≈ 4,669 201 609 102 990 671 853 203 820 466 201 61	постоянная Фейгенбаума	ТХ		1975
α	≈ 2,502 907 875 095 892 822 283 902 873 218 215 78	константа Фейгенбаума	ТХ		1975
C2	≈ 0,643 410 546 29	Константа Каэна	ТЧ	Т
C2	≈ 0,660 161 815 846 869 573 927 812 110 014 555 77	константа простых близнецов	ТЧ			5 020
M1	≈ 0,261 497 212 847 642 783 755 426 838 608 695 85	константа Майсселя — Мертенса	ТЧ		1866; 1874	8010
B2	≈ 1,902 160 583 104[3]	константа Бруна для простых близнецов	ТЧ		1919	10
B4	≈ 0,870 588 380 0	константа Бруна для простых четвёрок	ТЧ
	≈ 0,662 743 419 349 181 580 974 742 097 109 252 90	предел Лапласа	мат
G	≈ 0,915 965 594 177 219 015 054 603 514 932 384 11	постоянная Каталана	комб			31 026 000 000
Λ	0.22 ≥ Λ ≥ 0[4]	константа де Брёйна — Ньюмана	ТЧ		1950, 1976	0
K	≈ 0,764 223 653 589 220 66	константа Ландау — Рамануджана	ТЧ	И (?)		30 010
K	≈ 1,131 988 24	константа Висваната	ТЧ			16
K0	≈ 2,685 452 001 065	постоянная Хинчина	ТЧ		1934
J	≈ 3,058 198 247 456 354 132 564 564 787 888 767...	константа Поля — Гаусса	ТЧ			10343
B´L	1 (первоначальная гипотеза 1,08366[5])	константа Лежандра	ТЧ	Ц	1808	точное значение
λ	≈ 0,624 329 988 543 550 870 992 936	Постоянная Голомба — Дикмана	ТЧ
μ	≈ 1,451 369 234 883 381 050 283 968 485 892 027	константа Рамануджана — Солднера	ТЧ			75 500
E'B	≈ 1,606 695 152 415 291 763	константа Эрдёша — Борвейна	ТЧ	И
Ω	≈ 0,007 874 996 997 812 384 4	константа Хайтина	АИТ	Т
ζ(3)	≈ 1,202 056 903 159 594 285 399 738 161 511 449 99	постоянная Апери	ТЧ	И	1735	100 000 001 000
ɯ	≈ 0,739 085 133 215 160 641 655 312 087 673 873 40	число Дотти	ТХ
A	≈ 1,282 427 129 100 622 636 875 342 568 869 791 73	постоянная Глейшера — Кинкелина	ТЧ		1860
θ, A	≈ 1,306 377 883 863 080 690 468 614 492 6	Константа Миллса	ТЧ		1947	6850
ρ	≈ 1,324 717 957 244 746 025 960 908 854 478	Пластическое число	ТЧ	А, И	1928

См. также

• Постоянная
• Число