Теорема котангенсов

Теорема котангенсов — тригонометрическая теорема, связывающая радиус вписанной окружности треугольника с длиной его сторон. Теорему котангенсов удобно использовать при решении треугольника по трём сторонам.

Общий вид треугольника

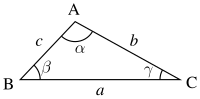
Формулировка

Пусть

${\displaystyle a,b,c}$ — длины трёх сторон треугольника,

${\displaystyle \alpha ,\beta ,\gamma }$ — углы, лежащие напротив, соответственно, сторон ${\displaystyle a,b,c}$,

${\displaystyle r}$ — радиус вписанной окружности треугольника и

${\displaystyle p={\frac {a+b+c}{2}}}$ — полупериметр треугольника.

Тогда справедливы следующие формулы:^[1]

${\displaystyle \mathrm {ctg} {\frac {\alpha }{2}}={\frac {p-a}{r}}}$,

${\displaystyle \mathrm {ctg} {\frac {\beta }{2}}={\frac {p-b}{r}}}$,

${\displaystyle \mathrm {ctg} {\frac {\gamma }{2}}={\frac {p-c}{r}}}$,

или эквивалентно:

${\displaystyle {\frac {p-a}{\mathrm {ctg} {\frac {\alpha }{2}}}}={\frac {p-b}{\mathrm {ctg} {\frac {\beta }{2}}}}={\frac {p-c}{\mathrm {ctg} {\frac {\gamma }{2}}}}=r}$.

Словами теорему можно сформулировать так: котангенс половинного угла равен разности отношения полупериметра и длины противолежащей стороны указанного угла к радиусу вписанной окружности.

Доказательство

Доказательство

.

Рассмотрим треугольник ${\displaystyle ABC}$ со вписанной окружностью - ${\displaystyle \omega (O,r)}$ ; сторонами ${\displaystyle AB,BC,AC}$ и углами ${\displaystyle \alpha ,\beta ,\gamma }$.

Так как точка пересечения биссектрис совпадает с центром вписанной окружности ${\displaystyle O}$ (см. инцентр) , проведем биссектрисы ${\displaystyle AO,BO,CO}$ и проведем радиусы ${\displaystyle OH_{1},OH_{2},OH_{3}}$ к сторонам ${\displaystyle AC,AB,BC}$ соответственно.

Рассмотрим треугольник ${\displaystyle AOH_{2}}$. По свойству радиуса вписанной окружности в треугольник , ${\displaystyle OH_{2}}$ перпендикулярно стороне ${\displaystyle AB}$, тогда треугольник ${\displaystyle AOH_{2}}$ - прямоугольный.

Так как бисcектриса ${\displaystyle AO}$ делит угол ${\displaystyle \alpha }$ на две равные части, то ${\displaystyle \angle H_{2}AO={\frac {\alpha }{2}}}$, тогда ${\displaystyle \mathrm {ctg} {(\angle H_{2}AO)}=\mathrm {ctg} {\frac {\alpha }{2}}={\frac {AH_{2}}{OH_{2}}}}$. Выразим радиус ${\displaystyle OH_{2}}$.

${\displaystyle OH_{2}=r={\frac {AH_{2}}{\mathrm {ctg} {\frac {\alpha }{2}}}}}$

Выразим ${\displaystyle AH_{2}}$ через ${\displaystyle AB}$

${\displaystyle AH_{2}=AB-BH_{2}}$

${\displaystyle BH_{2},BH_{3}}$ - касательные к окружности, проведенные из одной точки, тогда по свойству касательных ${\displaystyle BH_{2}=BH_{3}}$

Выразим ${\displaystyle BH_{3}}$ через ${\displaystyle BC}$

${\displaystyle BH_{3}=BC-CH_{3}}$

${\displaystyle CH_{3},CH_{1}}$ - касательные к окружности, проведенные из одной точки, тогда по свойству касательных ${\displaystyle CH_{3}=CH_{1}}$

Выразим ${\displaystyle CH_{1}}$ через ${\displaystyle AC}$

${\displaystyle CH_{1}=AC-AH_{1}}$

${\displaystyle AH_{1},AH_{2}}$ - касательные к окружности, проведенные из одной точки, тогда по свойству касательных ${\displaystyle AH_{1}=AH_{2}}$

Подставим все вместо ${\displaystyle AH_{2}}$.

${\displaystyle AH_{2}=AB-(BC-(AC-AH_{2}))=AB-BC+AC-AH_{2}}$

Выражая ${\displaystyle AH_{2}}$ получим

${\displaystyle AH_{2}={\frac {AB-BC+AC}{2}}={\frac {AB+BC+AC}{2}}-BC=p-BC}$

Подставим все в исходное уравнение

${\displaystyle r={\frac {p-BC}{\mathrm {ctg} {\frac {\alpha }{2}}}}}$

Аналогично рассматривая треугольники ${\displaystyle BOH_{3}}$ и ${\displaystyle COH_{2}}$, получим

${\displaystyle r={\frac {p-BC}{\mathrm {ctg} {\frac {\alpha }{2}}}}={\frac {p-AC}{\mathrm {ctg} {\frac {\beta }{2}}}}={\frac {p-AB}{\mathrm {ctg} {\frac {\gamma }{2}}}}}$.

Обобщение

В сферической тригонометрии существует похожая формула для половины угла, а также двойственная к ней формула половины стороны.

Следствия

Из теоремы котангенсов может быть получено выражение для радиуса вписанной окружности ${\displaystyle r={\sqrt {{\frac {1}{p}}(p-a)(p-b)(p-c)}}}$. Далее, так как площадь треугольника ${\displaystyle S=pr}$, из теоремы котангенсов следует формула Герона.

См. также

• Теорема косинусов
• Теорема о проекциях
• Теорема синусов
• Теорема тангенсов
• Тригонометрические тождества
• Тригонометрические функции
• Формулы Мольвейде