Функция распределения простых чисел

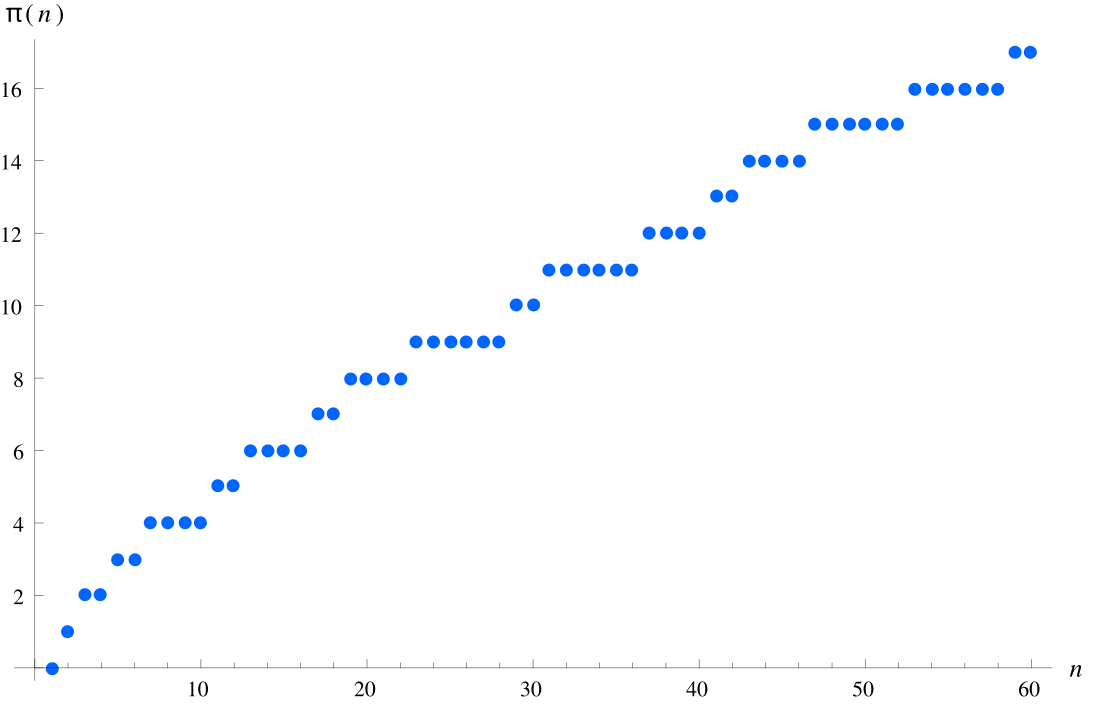
В математике функция распределения простых чисел, или пи-функция ${\displaystyle \pi (x)}$, — это функция, равная числу простых чисел, меньших либо равных действительному числу ${\displaystyle x}$ ^[1][2] (обозначение ${\displaystyle \pi (x)}$ никак не связано с числом пи).

Значения пи-функции для первых 60 натуральных чисел

История

Большой интерес в теории чисел представляет скорость роста пи-функции.^[3][4] В конце XVIII столетия Гауссом и Лежандром было выдвинуто предположение, что пи-функция оценивается величиной

${\displaystyle {\frac {x}{\ln x}}}$

в том смысле, что

${\displaystyle \lim \limits _{x\to +\infty }{\frac {\pi (x)}{x/\ln x}}=1.}$

Это утверждение — теорема о распределении простых чисел. Оно эквивалентно утверждению

${\displaystyle \lim \limits _{x\to +\infty }{\frac {\pi (x)}{\operatorname {li} (x)}}=1}$

где ${\displaystyle \operatorname {li} }$ — это интегральный логарифм. Теорема о простых числах была впервые доказана в 1896 Жаком Адамаром и независимо Валле-Пуссеном с использованием дзета-функции Римана, введенной Риманом в 1859. Точнее, рост ${\displaystyle \pi (x)}$ сейчас описывается формулой

${\displaystyle \pi (x)=\operatorname {li} (x)+O{\bigl (}xe^{-{\sqrt {\ln x}}/15}{\bigr )}.}$

Когда ${\displaystyle x}$ не сильно велико, ${\displaystyle \operatorname {li} (x)}$ больше, чем ${\displaystyle \pi (x)}$, однако разность ${\displaystyle \pi (x)-\operatorname {li} (x)}$ меняет свой знак бесконечное число раз. Наименьшее натуральное число, при котором происходит смена знака, называется числом Скьюза.

Доказательства теоремы о простых числах, не использующие дзета-функцию или комплексный анализ, были найдены в 1948 году Атле Сельбергом и Полом Эрдёшом (в основной части независимо).^[5]

Таблицы для функций π ( x ) , x ln ⁡ x , li ⁡ ( x ) {\displaystyle \pi (x),{\frac {x}{\ln x}},\operatorname {li} (x)}

В следующей таблице показан рост функций ${\displaystyle \pi (x),{\frac {x}{\ln x}},\operatorname {li} (x)}$ для ${\displaystyle x}$, равного степеням 10^[3][6][7][8].

x	π(x)	π(x) − x / ln x	li(x) − π(x)	x / π(x)	π(x)/x (доля простых чисел)
10	4	−0,3	2,2	2,500	40 %
102	25	3,3	5,1	4,000	25 %
103	168	23	10	5,952	16,8 %
104	1 229	143	17	8,137	12,3 %
105	9 592	906	38	10,425	9,59 %
106	78 498	6 116	130	12,740	7,85 %
107	664 579	44 158	339	15,047	6,65 %
108	5 761 455	332 774	754	17,357	5,76 %
109	50 847 534	2 592 592	1 701	19,667	5,08 %
1010	455 052 511	20 758 029	3 104	21,975	4,55 %
1011	4 118 054 813	169 923 159	11 588	24,283	4,12 %
1012	37 607 912 018	1 416 705 193	38 263	26,590	3,76 %
1013	346 065 536 839	11 992 858 452	108 971	28,896	3,46 %
1014	3 204 941 750 802	102 838 308 636	314 890	31,202	3,20 %
1015	29 844 570 422 669	891 604 962 452	1 052 619	33,507	2,98 %
1016	279 238 341 033 925	7 804 289 844 393	3 214 632	35,812	2,79 %
1017	2 623 557 157 654 233	68 883 734 693 281	7 956 589	38,116	2,62 %
1018	24 739 954 287 740 860	612 483 070 893 536	21 949 555	40,420	2,47 %
1019	234 057 667 276 344 607	5 481 624 169 369 960	99 877 775	42,725	2,34 %
1020	2 220 819 602 560 918 840	49 347 193 044 659 701	222 744 644	45,028	2,22 %
1021	21 127 269 486 018 731 928	446 579 871 578 168 707	597 394 254	47,332	2,11 %
1022	201 467 286 689 315 906 290	4 060 704 006 019 620 994	1 932 355 208	49,636	2,01 %
1023	1 925 320 391 606 803 968 923	37 083 513 766 578 631 309	7 250 186 216	51,939	1,92 %
1024	18 435 599 767 349 200 867 866	339 996 354 713 708 049 069	17 146 907 278	54,243	1,84 %
1025	176 846 309 399 143 769 411 680	3 128 516 637 843 038 351 228	55 160 980 939	56,546	1,77 %
1026	1 699 246 750 872 437 141 327 603	28 883 358 936 853 188 823 261	155 891 678 121	58,850	1,70 %
1027	16 352 460 426 841 680 446 427 399	267 479 615 610 131 274 163 365	508 666 658 006	61,153	1,64 %

Колонка значений ${\displaystyle \pi (x)}$ — это последовательность A006880 в энциклопедии целочисленных последовательностей OEIS, ${\displaystyle \pi (x)-\left\lfloor {\frac {x}{\ln x}}+0{,}5\right\rfloor }$ — последовательность A057835, а ${\displaystyle \lfloor \operatorname {li} (x)+0{,}5\rfloor -\pi (x)}$ — последовательность A057752.

Алгоритмы вычисления пи-функции

Простой способ найти ${\displaystyle \pi (x)}$, если ${\displaystyle x}$ не очень велико, — применить решето Эратосфена, выдающего простые числа, не превосходящие ${\displaystyle x}$, и подсчитать их.

Более продуманный способ вычисления ${\displaystyle \pi (x)}$ был дан Лежандром: если ${\displaystyle p_{1},p_{2},\ldots ,p_{k}}$ — различные простые числа, то число целых чисел, не превосходящих заданного числа ${\displaystyle x}$ и не делящихся на все ${\displaystyle p_{i}}$, представимо в виде

${\displaystyle \lfloor x\rfloor -\sum _{i}\left\lfloor {\frac {x}{p_{i}}}\right\rfloor +\sum _{i<j}\left\lfloor {\frac {x}{p_{i}p_{j}}}\right\rfloor -\sum _{i<j<k}\left\lfloor {\frac {x}{p_{i}p_{j}p_{k}}}\right\rfloor +\cdots }$

(где ${\displaystyle \lfloor \cdots \rfloor }$ обозначает целую часть). Следовательно, полученное число равно

${\displaystyle \pi (x)-\pi \left({\sqrt {x}}\right)+1,}$

если числа ${\displaystyle p_{1},p_{2},\ldots ,p_{k}}$ — это все простые числа, не превосходящие ${\displaystyle {\sqrt {x}}}$.

В 1870—1885 годах Эрнст Майссель в серии статей описал (и использовал) практический комбинаторный способ вычисления ${\displaystyle \pi (x)}$. Пусть ${\displaystyle p_{1},p_{2},\ldots ,p_{n}}$ — первые ${\displaystyle n}$ простых чисел. Обозначим через ${\displaystyle \Phi (m,n)}$ число натуральных чисел, не превосходящих ${\displaystyle m}$, которые не делятся ни на одно ${\displaystyle p_{i}}$. Тогда

${\displaystyle \Phi (m,n)=\Phi (m,n-1)-\Phi \left(\left[{\frac {m}{p_{n}}}\right],n-1\right).}$

Возьмем натуральное ${\displaystyle m}$, если ${\displaystyle n=\pi \left({\sqrt[{3}]{m}}\right)}$ и если ${\displaystyle \mu =\pi \left({\sqrt {m}}\right)-n}$, то

${\displaystyle \pi (m)=\Phi (m,n)+n(\mu +1)+{\frac {\mu ^{2}-\mu }{2}}-1-\sum _{k=1}^{\mu }\pi \left({\frac {m}{p_{n+k}}}\right).}$

Используя этот подход, Майссель вычислил ${\displaystyle \pi (x)}$ для ${\displaystyle x=5\cdot 10^{5};10^{6};10^{7};10^{8}}$.

В 1959 году Деррик Генри Лемер расширил и упростил метод Майсселя. Для действительного ${\displaystyle m}$ и натуральных ${\displaystyle n,k}$ пусть ${\displaystyle P_{k}(m,n)}$ — количество чисел, не превосходящих m и имеющих ровно k простых множителей, не превосходящих ${\displaystyle p_{n}}$, а ${\displaystyle P_{0}(m,n)=1}$. Тогда

${\displaystyle \Phi (m,n)=\sum _{k=0}^{+\infty }P_{k}(m,n)}$

где сумма явно всегда имеет конечное число ненулевых слагаемых. Пусть ${\displaystyle y}$ — целое, такое, что ${\displaystyle {\sqrt[{3}]{m}}\leqslant y\leqslant {\sqrt {m}}}$, и положим ${\displaystyle n=\pi (y)}$. Тогда ${\displaystyle P_{1}(m,n)=\pi (m)-n}$ и ${\displaystyle P_{k}(m,n)=0}$ при ${\displaystyle k\geqslant 3}$. Следовательно

${\displaystyle \pi (m)=\Phi (m,n)+n-1-P_{2}(m,n)}$

Вычисление ${\displaystyle P_{2}(m,n)}$ может быть получено следующим способом:

${\displaystyle P_{2}(m,n)=\sum _{y<p\leqslant {\sqrt {m}}}\left(\pi \left({\frac {m}{p}}\right)-\pi (p)+1\right)}$

С другой стороны, вычисление ${\displaystyle \Phi (m,n)}$ может быть выполнено с помощью следующих правил:

1. ${\displaystyle \Phi (m,0)=\lfloor m\rfloor }$
2. ${\displaystyle \Phi (m,b)=\Phi (m,b-1)-\Phi \left({\frac {m}{p_{b}}},b-1\right)}$

Используя этот метод и IBM 701, Лемер смог вычислить ${\displaystyle \pi \left(10^{10}\right)}$.

Дальнейшие усовершенствования этого метода получили Lagarias, Miller, Odlyzko, Deleglise и Rivat.^[9]

Китайский математик Hwang Cheng использовал следующие тождества:^[10]

${\displaystyle e^{(a-1)\Theta }f(x)=f(ax),}$

${\displaystyle J(x)=\sum _{n=1}^{\infty }{\frac {\pi (x^{1/n})}{n}}}$

и, полагая ${\displaystyle x=e^{t}}$, выполняя преобразование Лапласа обеих частей и применяя сумму геометрической прогрессии с ${\displaystyle e^{n\Theta }}$, получил выражение:

${\displaystyle {\frac {1}{2{\pi }i}}\int _{c-i\infty }^{c+i\infty }g(s)t^{s}\,ds=\pi (t)}$

${\displaystyle {\frac {\ln \zeta (s)}{s}}=(1-e^{\Theta (s)})^{-1}g(s)}$

${\displaystyle \Theta (s)=s{\frac {d}{ds}}}$

Другие функции, подсчитывающие простые числа

Другие функции, подсчитывающие простые числа, также используются, поскольку с ними удобнее работать. Одна из них — функция Римана, часто обозначаемая как ${\displaystyle \Pi _{0}(x)}$ или ${\displaystyle J_{0}(x)}$. Она испытывает прыжок на 1/n для степеней простых ${\displaystyle p^{n}}$, причем в точке прыжка ${\displaystyle x}$ её значение равно полусумме значений на обеих сторонах от ${\displaystyle x}$. Эти дополнительные детали нужны для того, чтобы она могла быть определена обратным преобразованием Меллина. Формально, мы определим ${\displaystyle \Pi _{0}(x)}$ как

${\displaystyle \Pi _{0}(x)={\frac {1}{2}}{\bigg (}\sum _{p^{n}<x}{\frac {1}{n}}\ +\sum _{p^{n}\leq x}{\frac {1}{n}}{\bigg )}}$

где p простое.

Мы также можем записать

${\displaystyle \Pi _{0}(x)=\sum \limits _{n=2}^{x}{\frac {\Lambda (n)}{\ln n}}-{\frac {1}{2}}{\frac {\Lambda (x)}{\ln x}}=\sum _{n=1}^{\infty }{\frac {1}{n}}\pi _{0}({\sqrt[{n}]{x}})}$

где ${\displaystyle \Lambda (n)}$ — функция Мангольдта и

${\displaystyle \pi _{0}(x)=\lim _{\varepsilon \rightarrow 0}{\frac {\pi (x-\varepsilon )+\pi (x+\varepsilon )}{2}}.}$

Формула обращения Мёбиуса дает

${\displaystyle \pi _{0}(x)=\sum _{n=1}^{\infty }{\frac {\mu (n)}{n}}\Pi _{0}({\sqrt[{n}]{x}})}$

Используя известное соотношение между логарифмом дзета-функции Римана и функцией Мангольдта ${\displaystyle \Lambda }$, и используя формулу Перрона мы получим

${\displaystyle \ln \zeta (s)=s\int _{0}^{\infty }\Pi _{0}(x)x^{-s-1}\,dx}$

Функция Римана имеет производящую функцию

${\displaystyle \sum _{n=1}^{\infty }\Pi _{0}(n)x^{n}=\sum _{a=2}^{\infty }{\frac {x^{a}}{1-x}}-{\frac {1}{2}}\sum _{a=2}^{\infty }\sum _{b=2}^{\infty }{\frac {x^{ab}}{1-x}}+{\frac {1}{3}}\sum _{a=2}^{\infty }\sum _{b=2}^{\infty }\sum _{c=2}^{\infty }{\frac {x^{abc}}{1-x}}-{\frac {1}{4}}\sum _{a=2}^{\infty }\sum _{b=2}^{\infty }\sum _{c=2}^{\infty }\sum _{d=2}^{\infty }{\frac {x^{abcd}}{1-x}}+\cdots }$

Функции Чебышёва — это функции, подсчитывающие степени простых чисел ${\displaystyle p^{n}}$ с весом ${\displaystyle \ln p}$:

${\displaystyle \theta (x)=\sum _{p\leqslant x}\ln p}$

${\displaystyle \psi (x)=\sum _{p^{n}\leqslant x}\ln p=\sum _{n=1}^{\infty }\theta ({\sqrt[{n}]{x}})=\sum _{n\leqslant x}\Lambda (n).}$

Формулы для функций, подсчитывающих простые числа

Формулы для функций, подсчитывающих простые числа, бывают двух видов: арифметические формулы и аналитические формулы. Аналитические формулы для таких функций были впервые использованы для доказательства теоремы о простых числах. Они происходят от работ Римана и Мангольдта и в общем известны как явные формулы.^[11]

Существует следующее выражение для ${\displaystyle \psi }$-функции Чебышёва:

${\displaystyle \psi _{0}(x)=x-\sum _{\rho }{\frac {x^{\rho }}{\rho }}-\ln 2\pi -{\frac {1}{2}}\ln(1-x^{-2})}$

где

${\displaystyle \psi _{0}(x)=\lim _{\varepsilon \rightarrow 0}{\frac {\psi (x-\varepsilon )+\psi (x+\varepsilon )}{2}}.}$

Здесь ${\displaystyle \rho }$ пробегает нули дзета-функции в критической полосе, где действительная часть ${\displaystyle \rho }$ лежит между нулем и единицей. Формула верна для всех ${\displaystyle x>1}$. Ряд по корням сходится условно, и может быть взят в порядке абсолютного значения возрастания мнимой части корней. Заметим, что аналогичная сумма по тривиальным корням дает последнее слагаемое в формуле.

Для ${\displaystyle \scriptstyle \Pi _{0}(x)}$ мы имеем следующую сложную формулу

${\displaystyle \Pi _{0}(x)=\operatorname {li} (x)-\sum _{\rho }\operatorname {li} (x^{\rho })-\ln 2+\int _{x}^{\infty }{\frac {dt}{t(t^{2}-1)\ln t}}.}$

Опять же, формула верна для всех ${\displaystyle x>1}$, где ${\displaystyle \rho }$ — нетривиальные нули зета-функции, упорядоченные по их абсолютному значению, и, снова, последний интеграл берется со знаком «минус» и является такой же суммой, но по тривиальным нулям. Выражение ${\displaystyle \operatorname {li} (x^{\rho })}$ во втором члене может быть рассмотренно как ${\displaystyle \operatorname {Ei} (\rho \ln x)}$, где ${\displaystyle \operatorname {Ei} }$ — это аналитическое продолжение интегральной показательной функции на комплексную плоскость с ветвью, вырезанной вдоль прямой ${\displaystyle x<0}$.

Таким образом, формула обращения Мёбиуса дает нам^[12]

${\displaystyle \pi _{0}(x)=\operatorname {R} (x)-\sum _{\rho }\operatorname {R} (x^{\rho })-{\frac {1}{\ln x}}+{\frac {1}{\pi }}\mathop {\mathrm {arctg} } {\frac {\pi }{\ln x}}}$

верное для ${\displaystyle x>1}$, где

${\displaystyle \operatorname {R} (x)=\sum _{n=1}^{\infty }{\frac {\mu (n)}{n}}\operatorname {li} (x^{1/n})=1+\sum _{k=1}^{\infty }{\frac {(\ln x)^{k}}{k!k\zeta (k+1)}}}$

называется R-функцией также в честь Римана.^[13] Последний ряд в ней известен как ряд Грама^[14] и сходится для всех ${\displaystyle x>0}$.

Сумма по нетривиальным нулям дзета-функции в формуле для ${\displaystyle \pi _{0}(x)}$ описывает флуктуации ${\displaystyle \pi _{0}(x)}$, в то время как остальные слагаемые дают гладкую часть пи-функции,^[15] поэтому мы можем использовать

${\displaystyle \operatorname {R} (x)-{\frac {1}{\ln x}}+{\frac {1}{\pi }}\mathop {\mathrm {arctg} } {\frac {\pi }{\ln x}}}$

как наилучшее приближение для ${\displaystyle \pi (x)}$ для ${\displaystyle x>1}$.

Амплитуда «шумной» части эвристически оценивается как ${\displaystyle {\sqrt {x}}/\ln x}$, поэтому флуктуации в распределении простых могут быть явно представлены ${\displaystyle \Delta }$-функцией:

${\displaystyle \Delta (x)=\left(\pi _{0}(x)-\operatorname {R} (x)+{\frac {1}{\ln x}}-{\frac {1}{\pi }}\mathop {\mathrm {arctg} } {\frac {\pi }{\ln x}}\right){\frac {\ln x}{\sqrt {x}}}.}$

Обширные таблицы значений ${\displaystyle \Delta (x)}$ доступны здесь.^[7]

Неравенства

Здесь выписаны некоторые неравенства для ${\displaystyle \pi (x)}$.

${\displaystyle {\frac {x}{\ln x}}<\pi (x)<1{,}25506\cdot {\frac {x}{\ln x}}\qquad x\geqslant 17.}$

Левое неравенство выполняется при ${\displaystyle x\geqslant 17}$, а правое — при ${\displaystyle x>1.}$^[16]

Неравенства для ${\displaystyle n}$-го простого числа ${\displaystyle p_{n}}$:

${\displaystyle n\ln n+n\ln \ln n-3/2\cdot n<p_{n}<n\ln n+n\ln \ln n,\ n\geqslant 6.}$

Левое неравенство верно при ${\displaystyle n\geqslant 2}$, а правое — при ${\displaystyle n\geqslant 6}$.

Имеет место следующая асимптотика для ${\displaystyle n}$-го простого числа ${\displaystyle p_{n}}$:

${\displaystyle p_{n}=n\ln n\left(1+{\frac {\ln \ln n-1}{\ln n}}+{\frac {\ln \ln n-2}{\ln ^{2}n}}+{\frac {-1/2\ln ^{2}\ln n+3\ln \ln n-11/2}{\ln ^{3}n}}+O\left({\frac {\ln ^{3}\ln n}{\ln ^{4}n}}\right)\right)}$

Гипотеза Римана

Основная статья: Гипотеза Римана

Гипотеза Римана эквивалентна более точной границе ошибки приближения ${\displaystyle \pi (x)}$ интегральным логарифмом, а отсюда и более регулярному распределению простых чисел

${\displaystyle \pi (x)=\operatorname {li} (x)+O({\sqrt {x}}\ln x).}$

В частности,^[17]

${\displaystyle |\pi (x)-\operatorname {li} (x)|<{\frac {1}{8\pi }}{\sqrt {x}}\,\ln x,\qquad x\geqslant 2657.}$

См. также

• Теорема о распределении простых чисел
• Постулат Бертрана
• Число Скьюза