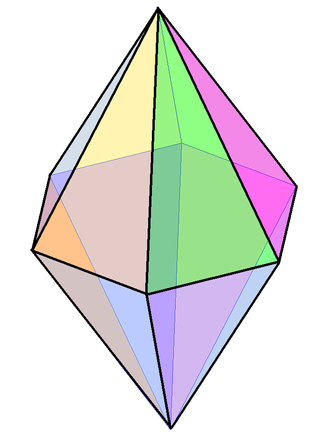
இரட்டைப் பட்டைக்கூம்பு

ஒரு (சமச்சீர்) n-கோண இருபட்டைக்கூம்பு அல்லது n-கோண இரட்டைப்பட்டைக்கூம்பு (bipyramid, dipyramid) என்பது ஒரு n-கோண பட்டைக்கூம்பையும் அதன் ஆடிபிம்பத்தையும் அவற்றின் அடிப்பக்கங்கள் ஒன்றுடன் ஒன்று ஒட்டியவாறு இணைத்து உருவாக்கப்படும் பன்முகியாகும்.^{[3] [4]} ஒரு n-கோண இருபட்டைக்கூம்பு, 2n முக்கோண முகங்கள், 3n விளிம்புகள் 2 + n உச்சிகளைக் கொண்டிருக்கும்.

இரும-சீர் n-கோண இருபட்டைக்கூம்புகளின் கணம்
இரும-சீர் அறுகோண இருபட்டைக்கூம்பு
Type	இருமம்-சீர்திண்மம் (இருமம்-அரை ஒழுங்கு பன்முகி)
கோஎக்சிட்டர் வரைபடம்
இசுலாபிலிக் குறியீடு	{ } + {n}[1]
முகங்கள்	2n சர்வசம இருசமபக்க முக்கோணங்கள்
விளிம்புகள்	3n
உச்சிகள்	2 + n
முக அமைவு	V4.4.n
சமச்சீர்மை குலம்	Dnh]], [n,2], (*n22), order 4n
சுழற்சி குலம்	Dn, [n,2]+, (n22), order 2n
இருமப் பன்முகி	(குவிவு) சீர்பன்முகி n-கோணப் பட்டகம்
பண்புகள்	குவிவு, முக-கடப்பு, ஒழுங்கு உச்சிகள்[2]
வலையமைப்பு	ஐங்கோண இருபட்டைக்கூம்பின் வலையமைப்பு (n = 5)

உறிகோல் மற்றும் நொய்லி வளையங்கள் கொண்டு உருவாக்கப்பட்ட இருபட்டைக்கூம்பு

"ஒழுங்கு", நேர் இருபட்டைக்கூம்புகள்

ஒரு "ஒழுங்கு" இருபட்டைக்கூம்பின் அடிப்பக்கம் ஒழுங்கு பல்கோணமாக இருக்கும். இது ஒரு நேர் இருபட்டைக்கூம்பாகக் கொள்ளப்படுகிறது..

ஒரு நேர் இருபட்டைக்கூம்பின் மேலுச்சிகள் இரண்டில் ஒன்று பல்கோண அடியின் மையம் அல்லது திணிவு மையத்திற்கு நேர் மேற்புறத்திலும் மற்றொன்று நேர் கீழ்ப்புறத்திலும் அமைந்திருக்கும்.

ஒரு ஒழுங்கு நேர் (சமச்சீர்) n-கோண இருபட்டைக்கூம்பின் இசுலாபிலிக் குறியீடு: :{ } + {n}.

ஒரு நேர் (சமச்சீர்) இருபட்டைக்கூம்பின் இசுலாபிலிக் குறியீடு:

{ } + P. P - அடிப்பக்கப் பல்கோணத்தைக் குறிக்கிறது.

ஒழுங்கு உச்சிகளுடைய, "ஒழுங்கு" நேர் n-கோண இருபட்டைக்கூம்பானது^[2] n-கோண சீர் பட்டகத்தின் இருமமாகவும் சர்வசம இருசமபக்க முக்கோண முகங்களையும் கொண்டிருக்கும்.

ஒரு "ஒழுங்கு" நேர் (சமச்சீர்) n-கோண கோள இருபட்டைகூம்பைப் போல, ஒரு ஒழுங்கு நேர் (சமச்சீர்) n-கோண இருபட்டைக்கூம்பை ஒரு கோளத்தின் மீது தொலைவுக் குறுக்கம் செய்யலாம்: ஒரு துருவத்திலிருந்து மற்றொரு துருவத்துக்குச் செல்லும் சம இடைவெளியிலமைந்த n நிலநிரைக்கோடுகள் மற்றும் அவற்றை இருசமக்கூறிடும் நிலநடுக் கோடு.

"ஒழுங்கு" நேர் (சமச்சீர்) n-கோண இரட்டைப் பட்டைக்கூம்புகள்:

இரட்டைப் பட்டைக்கூம்பு பெயர்	இருகோண இரட்டைப் பட்டைக்கூம்பு	முக்கோண இரட்டைப் பட்டைக்கூம்பு (J12)	சதுர இரட்டைப் பட்டைக்கூம்பு (O)	ஐங்கோண இரட்டைப் பட்டைக்கூம்பு (J13)	அறுகோண இரட்டைப் பட்டைக்கூம்பு	எழுகோண இரட்டைப் பட்டைக்கூம்பு	எண்கோண இரட்டைப் பட்டைக்கூம்பு	நவகோண இரட்டைப் பட்டைக்கூம்பு	தசகோண இரட்டைப் பட்டைக்கூம்பு	...	முடிவிலா இரட்டைப் பட்டைக்கூம்பு]]
பன்முகியின் படிமம்		படிமம்:Triangular bipyramid.svg								...
கோளப் பாவுமை படிமம்										தரைபாவுமை படிமம்
முக அமைவு	V2.4.4	V3.4.4	V4.4.4	V5.4.4	V6.4.4	V7.4.4	V8.4.4	V9.4.4	V10.4.4	...	V∞.4.4
கோஎக்சிட்டெர் வரைபடம்										...

சமபக்க முக்கோண இருபட்டைக்கூம்புகள்

சமநீளமுள்ள விளிம்புகள் கொண்ட இருபட்டைக்கூம்புகளில் "ஒழுங்கு" நேர் (சமச்சீர்) முக்கோண, நான்கோண, ஐங்கோண இருபட்டைக்கூம்புகளென மூன்று வகைகள் உள்ளன. இதில் சமநீள விளிம்புகள் கொண்ட நான்முக அல்லது சதுர இருபட்டைக்கூம்பு பிளேட்டோவின் சீர்திண்மமாகவும், சமநீள விளிம்புடைய முக்கோண, ஐங்கோண இருபட்டைக்கூம்புகள் ஜான்சன் சீர்திண்மங்களிலும் அடங்கும் (J₁₂ and J₁₃).

சமபக்க முக்கோண இருபட்டைக்கூம்புகள்:

"ஒழுங்கு" நேர் (சமச்சீர்) இருபட்டைக்கூம்பின் பெயர்:	முக்கோண இருபட்டைக்கூம்பு (J12)	நான்கோண இருபட்டைக்கூம்பு எண்கோணி	ஐங்கோண இருபட்டைக்கூம்பு (J13)
படிமம்:

கன அளவு

இருபட்டைக்கூம்பின் (சமச்சீர்) கன அளவு: $${\displaystyle V={\frac {2}{3}}Bh\,,}$$ இதில் B என்பது அடிப்பக்கத்தின் பரப்பளவு; h என்பது அடிப்பக்கத் தளத்திலிருந்து மேலுச்சியின் செங்குத்து உயரம்.

இருபட்டைக்கூம்புகளின் அடிப்பக்கத்தின் வடிவமும் மேலுச்சியின் அமைவிடமும் எவ்வாறாக இருந்தாலும் இந்தக் கனவளவுக்கான வாய்பாடு பொருந்தும்; ஆனால் செங்குத்து உயரம் h ஆனது, அடிப் பல்கோணத்தின் உட்தளத்திலிருந்து மேலுச்சிக்கு அளவிடப்பட வேண்டும்.

எனவே ஒரு ஒழுங்கு இருபட்டைக்கூம்பின் அடிப்பக்கம் பக்க நீளம் s கொண்ட n-பக்கப் பல்கோணம்; அதன் உயரம் h எனில் அந்த இருபட்டைக்கூம்பின் கனவளவு: $${\displaystyle V={\frac {n}{6}}hs^{2}\cot {\frac {\pi }{n}}\,.}$$

சாய்வு இரட்டைப் பட்டைக்கூம்பு

நேரற்ற இருபட்டைக்கூம்புகள், சாய்வு இருபட்டைக்கூம்புகள் (oblique bipyramids) எனப்படும்.

குவிவிலா இருபட்டைக்கூம்புகள்

குவிவிலாப் பல்கோண அடிப்பக்கம் கொண்ட இருபட்டைக்கூம்பானது குழிவு இருபட்டைக்கூம்பு (concave bipyramid) அல்லது குவிவிலா இருபட்டைக்கூம்பு எனப்படுகிறது.

குவிவிலா (சமச்சீர்) நான்கோண இருபட்டைக்கூம்பு (*)

(*) இதன் அடிப்பக்கத்திற்கு மையம் கிடையாது; இதன் உச்சிகள் அடிப்பக்கத்தின் மையத்திற்கு நேரெதிராக மேலும் கீழுமாக அமையாவிட்டால் இது ஒரு நேர் இருபட்டைக்கூம்பாக இருக்காது. எனினும் ஒரு குவிவிலா எண்முகியாக இருக்கும்.

சமச்சீரற்ற/தலைகீழ் நேர் இருபட்டைக்கூம்புகள்

சமச்சீரற்ற நேர் பட்டைக்கூம்பு என்பது சர்வசம அடிப்பக்கங்களும் சமமற்ற உயரங்களுமுடைய இரு நேர் பட்டைக்கூம்புகளின் அடிப்பக்கங்கள் பொருத்தப்பட்ட இணைப்பாகும்.

தலைகீழ் நேர் இரட்டைப் பட்டைக்கூம்பு என்பது சர்வசம அடிப்பக்கங்களும் சமமற்ற உயரங்களும் கொண்ட இரு நேர் பட்டைக்கூம்புகளை அடியோடு அடியாகவும் ஆனால் பொது அடிப்பக்கத்தின் ஒரே பக்கமாக இணைக்கக் கிடைக்கும் வடிவமாகும்.

சமச்சீரற்ற/தலைகீழ் நேர் இருபட்டைக்கூம்பின் இருமம் ஒரு அடிக்கண்டமாகும்.

"ஒழுங்கு" சமச்சீரற்ற/தலைகீழ் நேர் n-கோண இருபட்டைக்கூம்பின் சமச்சீர்மை குலம் C_nv (வரிசை: 2n).

"ஒழுங்கு" சமச்சீரற்ற/தலைகீழ் நேர் அறுகோண இருபட்டைக்கூம்புகள்

சமச்சீரற்ற	தலைகீழ்

"ஒழுங்கு" நாள்மீன் இருபட்டைக்கூம்புகள்

தனக்குத்தானே வெட்டிக்கொள்ளும் அல்லது நாள்மீன் இருபட்டைக்கூம்பு, நாள்மீன் பல்கோணியை அடிப்பக்கமாகக் கொண்டிருக்கும்.

ஒரு ஒழுங்கு நாள்மீன் பல்கோணியை அடிப்பக்கமாகவும், அதன் மையத்திற்கு நேரெதிராக மேலும் கீழும் இரு உச்சிகளுடனும் அமைந்தவாறு, ஒன்றுக்கொன்று சமச்சீர் முக்கோண முகங்களை அடிப்பக்கத்தின் ஒவ்வொரு விளிம்புடனும் ஒவ்வொரு உச்சியையும் இணைத்து "ஒழுங்கு" நேர் சமச்சீர் நாள்மீன் இருபட்டைக்கூம்பை உருவாக்கலாம்.

ஒரு "ஒழுங்கு" சமச்சீர் நாள்மீன் இருபட்டைக்கூம்பின் முகங்கள், சர்வசம இருசமபக்க முக்கோணங்களாக இருக்கும்.

{p/q}-இருபட்டைக்கூம்பின் கோஎக்சிட்டர் வரைபடம்: .

"ஒழுங்கு" சமச்சீர் நாள்மீன் இருபட்டைக்கூம்புகள்:

நாள்மீன் பல்கோணி அடி	5/2]]-கோணி	7/2-கோணி	7/3-கோணி	8/3-கோணி	9/2-கோணி	9/4-கோணி
நாள்மீன் இருபட்டைக்கூம்பின் படிமம்
கோஎக்சிட்டர் வரைபடம்

"ஒழுங்கு" நேர் சமச்சீர் நாள்மீன் இருபட்டைக்கூம்புகள்:

நாள்மீன் பல்கோணி அடி	10/3-கோணி	11/2-கோணி	11/3-கோணி	11/4-கோணி	11/5-கோணி	12/5-கோணி
நாள்மீன் இருபட்டைக்கூம்பின் படிமம்
கோஎக்சிட்டர் வரைபடம்