சார்பு

கணிதத்தில் சார்பு (function^[1]) என்பது ஒரு கணத்திலுள்ள ஒவ்வொரு உறுப்பையும் மற்றொரு கணத்திலுள்ள ஒரேயொரு உறுப்போடு இணைக்கும் ஒரு தொடர்பாகும். முதல் கணம் சார்பின் ஆட்களம் என்றும் இரண்டாவது கணம் சார்பின் இணையாட்களம் என்றும் அழைக்கப்படும். ஆட்களத்தின் உறுப்புகள் உள்ளீடுகள் எனவும் இவ்வுள்ளீடுகளோடு இணைக்கப்படும் இணை ஆட்களத்திலுள்ள உறுப்புகள் வெளியீடுகள் எனவும் அழைக்கப்படுகின்றன. அனைத்து வெளியீடுகளைக் கொண்ட கணம் சார்பின் வீச்சு அல்லது எதிருரு எனப்படும்.

சிவப்பு நிற வளைவரை கார்ட்டீசியன் தளத்தில் வரையப்பட்ட f சார்பின் வரைபடம். இவ்வளைவரையின் மீதமையும் புள்ளிகளின் அச்சுதூரங்கள் (x,f(x)) ஓர் உள்ளீட்டிற்கு ஒரேயொரு வெளியீடு என்ற சார்பின் கட்டுப்பாட்டை வடிவவியல் முறையில், ஒவ்வொரு நிலைக்குத்துக் கோடும் (ஆதிப்புள்ளி வழியே வரையப்பட்ட மஞ்சள் வண்ண நிலைக்குத்துக் கோடு) வளைவரையை ஒரேயொரு புள்ளியில் மட்டுமே சந்திக்கிறது என்பதைக் கொண்டு உணரலாம்.

பொதுவாக சார்பு f என்ற குறிகொண்டு குறிக்கப்படும். சார்பைக் குறிக்கும் ஆங்கிலச் சொல்லான function என்பதின் முதல் எழுத்தே இக்குறி.

சார்புகளுக்கு ஓர் எளிய எடுத்துக்காட்டு:

f(x) = x²

இத்தொடர்பின்படி,

ஒவ்வொரு உள்ளீடு x -ம் அதன் வர்க்கத்துடன் தொடர்புபடுத்தப்படுகிறது.

உள்ளீடு x -ன் f -ஐப் பொறுத்த வெளியீடு f(x) (வாசித்தல்: "f of x")

உள்ளீடு –3 எனில், அதற்குரிய வெளியீடு 9. அதாவது f(–3) = 9.

ஒரு சார்பின் உள்ளீடு சார்பின்மாறி (argument) என்றும் அந்த உள்ளீட்டிற்குரிய வெளியீடு சார்பின் மதிப்பு என்றும் அழைக்கப்படும்.

ஒரு சார்பின் உள்ளீடுகளும் வெளியீடுகளும் எப்பொழுதும் எண்களாகவே இருக்க வேண்டும் என்பது அவசியமில்லை. அவை எந்தவொரு கணங்களின் உறுப்புகளாகவும் அமையலாம். எடுத்துக்காட்டாக, வடிவவியல் வடிவங்களின் பக்கங்களின் எண்ணிக்கை என்ற சார்பு ஒரு முக்கோணத்தை எண் மூன்றுடனும் சதுரத்தை எண் நான்குடனும், .... தொடர்புபடுத்தும்.

ஒரு சார்பினைப் பலவிதங்களில் குறிக்கலாம்:

• சார்புகளை வாய்ப்பாடு அல்லது விதி மூலமாகக் குறிக்கலாம். அவ்வாய்ப்பாடு தரப்பட்ட உள்ளீடிற்குரிய வெளியீட்டைக் கணிப்பது எவ்வாறு என்பதை விளக்கும்.
• சார்புகளை வரைபடங்கள் மூலமாகக் குறிக்கலாம்.
• அறிவியலில் சில சார்புகள் அட்டவணை வடிவில் தரப்படுகின்றன.
• ஒரு சார்பினைப் பிற சார்புகளுடன் அதுகொண்ட தொடர்புகள் மூலமாகக் குறிக்கலாம். எடுத்துக்காட்டு: நேர்மாறுச் சார்பு, ஒரு வகையீட்டுச் சார்பின் தீர்வு.
• எண்கணித்தின் கூட்டல், கழித்தல், பெருக்கல் மற்றும் வகுத்தல் செயல்களைச் சார்புகளாக வரையறுக்கலாம்.
• சார்புகளில் வரையறுக்கப்படும் மற்றொரு முக்கியமான செயல் சார்புகளின் தொகுப்பு. இச்செயலில் ஒரு சார்பின் வெளியீடு மற்றொரு சார்பின் உள்ளீடாக அமையும்.
• ஒரு சார்பின் உள்ளீடும் அதற்குரிய வெளியீடும் ஒரு வரிசைச் சோடியாக குறிக்கப்படலாம்.

எடுத்துக்காட்டாக மேலே தரப்பட்ட எடுத்துக்காட்டில் உள்ள வரிசைச் சோடிகள்: <x, x²> (<–3, 9>). இந்த வரிசைச் சோடிகளைக் கார்ட்டீசியன் தளத்தில் வரையப்பட்ட சார்பின் வரைபடத்தின் மீதமைந்த ஒரு புள்ளிகளின் அச்சுத்தூரங்களாகக் கருதலாம்.

சம ஆட்களமும் சம இணை ஆட்களங்களும் கொண்ட அனைத்து சார்புகளும் கொண்ட கணம் சார்பு வெளி எனப்படும். சார்பு வெளியின் பண்புகளைப் பற்றி மெய்ப் பகுப்பியலிலும் மெய்ப்புனைப் பகுப்பியலிலும் அலசப்படுகிறது.

உள்ளுணர்வான விளக்கம்

ƒ என்ற சார்பு உள்ளீடு  x -ஐ எடுத்துக்கொண்டு வெளியீடு ƒ(x) -ஐத் திருப்பித் தருகிறது.

சார்புகள் பொதுவாக ஒரு உள்ளீட்டை எடுத்துக்கொண்டு அதனை வெளியீடாக மாற்றும் ஒரு இயந்திரத்தைப் போன்றதாகக் கருதப்படுகிறது. பெரும்பாலும் உள்ளீடுகள்  x அல்லது  t (உள்ளீடுகள் நேரமாக இருந்தால்) எனக் குறிக்கப்படுகின்றன. வெளியீடுகள்  y எனக் குறிக்கப்படுகின்றன. சார்பு, f எனக் குறிக்கப்படுகிறது.

y = f(x) என்ற குறியீடு, f என்ற சார்பு x என்ற உள்ளீட்டையும் y என்ற வெளியீட்டையும் கொண்டுள்ளது என்பதைக் கூறுகிறது.

y=f(x) -ல், y சார் மாறியாகும், x சாரா மாறியாகும்.

அடிக்கடிப் பயன்படுத்தப்படும் சார்புகளுக்குச் சிறப்புப் பெயர்கள் அளிக்கப்படுகின்றன. எடுத்துக்காட்டாக:

ஒரு மெய்யெண் x -ன் சிக்னம் சார்பு பின்வருமாறு வரையறுக்கப்படுகிறது:

${\displaystyle \operatorname {sgn}(x)={\begin{cases}-1&{\text{if }}x<0,\\0&{\text{if }}x=0,\\1&{\text{if }}x>0.\end{cases}}}$

ஒரு சார்பின் அனுமதிக்கப்பட்ட உள்ளீடுகளின் கணம் சார்பின் ஆட்களம் எனவும் கிடைக்கக் கூடிய வெளியீடுகளின் கணம் சார்பின் வீச்சு அல்லது சார்பின் எதிருரு எனவும் அழைக்கப்படும். வீச்சை உட்கணமாகக் கொண்ட கணம் சார்பின் இணையாட்களம் எனவும் அழைக்கப்படுகின்றன.

எடுத்துக்காட்டாக, f(x) = x² சார்பின் ஆட்களம் மெய்யெண்கள் கணம் எனில் அதன் வீச்சகம் எதிரிலா மெய்யெண்களின் கணமாகவும் இணையாட்களம் மெய்யெண்களின் கணமாகவும் அமையும். இச்சார்பு f -ஐ மெய்யெண்கள் மீதான மெய்மதிப்புச் சார்பு எனப்படும்.

ஆட்களம் மற்றும் இணையாட்களத்தைக் குறிப்பிடாமல் ஒரு "f ஒரு சார்பு" என்று மட்டும் சொன்னால் போதாது.

${\displaystyle f(x)={\sqrt {x^{2}-5x+6}}}$ என்ற வாய்ப்பாடு முறையாக வரையறுக்கப்பட்ட சார்பு அல்ல.

இதன் ஆட்களத்தை மெய்யெண் கணம் R -ன் உட்கணம், x ≤ 2 அல்லது x ≥ 3 ஆகவும் இணை ஆட்களத்தை R ஆகவும் எடுத்துக்கொண்டால்தான் இது ஒரு சார்பாக அமையும்.^[2]

வெவ்வேறு வாய்ப்பாடுகள் ஒரே சார்பைக் குறிக்கலாம். எடுத்துக்காட்டாக f(x) = (x + 1) (x − 1) மற்றும் f(x) = x² − 1 இரண்டும் ஒரே சார்பையே குறிக்கின்றன.^[3] மேலும் ஒரு சார்பானது வாய்ப்பாட்டினால் மட்டுமே குறிக்கப்பட வேண்டியதோ அல்லது எண்கள் சம்பந்தப்பட்டதாக மட்டுமே அமைய வேண்டும் என்பதோ இல்லை. சார்புகளின் ஆட்களங்களும் இணையாட்களங்களும் எந்தவொரு கணமாகவும் இருக்கலாம். உள்ளீடுகளாக தமிழ் வார்த்தைகளையும் வெளியீடுகளாக அவற்றின் முதலெழுத்துக்களையும் கொண்ட சார்பை இதற்கு எடுத்துக்காட்டாகக் காட்டலாம்.

சாதாரணமாகப் பார்த்தால், ஒரு சார்பை X கணத்திலுள்ள ஒவ்வொரு உறுப்பு x -உடனும் Y கணத்திலுள்ள ஒரேயொரு உறுப்பு y -ஐ இணைக்கும் ஒரு விதி எனலாம்.^[4][5][6] ஆயினும் சார்பை ஒரு விதியாகக் கருதுவது அவ்வளவு துல்லியமானதல்ல.^[7] விதி அல்லது இணைப்பது என்ற சொற்கள் ஏற்கனவே வரையறுக்கப்படாமல் இருப்பதே இம்முறையில் ஒரு சார்பை வரையறுப்பதில் உள்ள குறைபாடு. இவ்வகையான சார்பின் விளக்கம் சாதாரணமாகப் பார்க்கும் போது பொருத்தமாகத் தோன்றினாலும் தருக்கரீதியாக நுட்பமானதல்ல.^[8]

பல புத்தகங்களில், குறிப்பாகப் பாடப்புத்தகங்களில் இம்முறைசாரா வரையறை பயன்படுத்தப்பட்டாலும் உள்ளீடுகளும் வெளியீடுகளும் எப்படியும் வரிசைப்படுத்தப்பட்ட சோடிகளாக அமைகின்றன என்பது கவனிக்கத் தக்கது.^[9][10].

ஒரு சார்பினை பின்வரும் பண்புகள் கொண்டவரிசைச்சோடிகளாலான தொகுப்பாக விவரிக்கலாம்:

• (a, b) மற்றும் (a, c) இரண்டும் அத்தொகுப்பில் இருந்தால், b = c. அதாவது சோடிகளின் தொகுப்பில் ஒரே முதல் உறுப்பைக் கொண்ட இரண்டு வெவ்வேறான சோடிகள் இருக்காது.
• x என்ற உறுப்பு, சார்பு f -ன் ஆட்களத்தில் இருந்தால் (x, y) என்ற வரிசைச் சோடி f -ல் உள்ளவாறு ஒரு தனித்த  y ஒன்று இருக்கும். இந்த தனித்த  y, f(x) எனக் குறிக்கப்படுகிறது.^[11]

முறையான வரையறை

இப்படம் விளக்கும் சார்பின் ஆட்களம்: ${\displaystyle \{1,2,3\}}$, இணையாட்களம்: ${\displaystyle \{A,B,C,D\}}$ வரிசைச் சோடிகள்: ${\displaystyle \{(1,D),(2,C),(3,C)\}}$, வீச்சகம்: ${\displaystyle \{C,D\}}$

.

இதில் எண் 2, ஒன்றுக்கு மேற்பட்ட வரிசைச் சோடிகளின் முதல் உறுப்பாக வருவதால் இப்படம் குறிப்பது ஒரு சார்பல்ல. ((2, B) and (2, C))

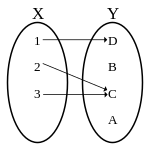
தரப்பட்ட இரு கணங்கள் X மற்றும் Y என்க.

X கணத்திலுள்ள ஒவ்வொரு உறுப்பு x -க்கும் Y கணத்தில் அமையும் தனித்ததொரு உறுப்பு y இரண்டையும் கொண்ட வரிசைச் சோடிகள் (x, y) அனைத்தையும் உறுப்புகளாகக் கொண்ட கணம் Fஆனது, X லிருந்து Y -க்கு வரையறுக்கப்பட்ட ஒரு சார்பாகும்.^[12]

எடுத்துக்காட்டாக, (x, x²), (x ஒரு மெய்யெண்) என்ற வரிசைச் சோடிகளின் கணம் மெய்யெண்கணத்திலிருந்து மெய்யெண்கணத்திற்கு வரையறுக்கப்பட்ட ஒரு சார்பாகும்.

மெய்யெண்கணத்திலிருந்து மெய்யெண்கணத்திற்கு வரையறுக்கப்படும் வர்க்கப்படுத்தும் சார்பும், மெய்யெண்கணத்திலிருந்து எதிரில்லா மெய்யெண்கணத்திற்கு வரையறுக்கப்படும் வர்க்கப்படுத்தும் சார்பும் ஒன்றல்ல. இரண்டும் வெவ்வேறானவை.

இவ்வகையாக சார்புகளை வரையறுப்பதில் இரு வெவ்வேறான விதங்கள் உள்ளன. ஆட்களமும் இணையாட்களமும் வெளிப்படையாக அல்லது மறைமுகமாக குறிக்கப்படலாம்.

முதல் வகை வரையறை:

இதில் சார்பின் வரையறையில் வரிசைப்படுத்தப்பட்ட மூன்று உறுப்புகள் உள்ளன:

(X, Y, F)

X -ஆட்களம்;

Y -துணை ஆட்களம்;

F - (x, y) வரிசைச்சோடிகளின் கணம்.^[13]

ஒவ்வொரு வரிசைச் சோடியிலும் முதல் உறுப்பு ஆட்களத்திலும் இரண்டாவது உறுப்பு இணையாட்களத்திலும் அமையும். மேலும் ஆட்களத்தின் ஒவ்வொரு உறுப்பும் ஒரேயொரு வரிசைச்சோடியின் முதல் உறுப்பாக இருத்தல் வேண்டும் என்பது ஒரு தேவையான கட்டுப்பாடாகவும் இருக்கும்.

இரண்டாம் வகை வரையறை:

இவ்வகையில் வரிசைப்படுத்தப்பட்ட சோடிகளைக் கொண்ட கணமாக சார்பு வரையறுக்கப்படுகிறது.

இவ்வரிசைச் சோடிகளில் முதல் உறுப்பாக அமைவது ஒரேயொரு வரிசைச் சோடியில் மட்டுமே வரலாம்.

வரிசைச் சோடிகளின் முதல் உறுப்புகளாலான கணம் சார்பின் ஆட்களம்.

இரண்டாவது உறுப்புகளாலான கணம் சார்பின் எதிருரு அல்லது வீச்சு.

இணையாட்களத்தைப் பற்றி எந்த விவரமும் தரப்படவில்லை.^[14][15]

தொடர்பு:

சார்புகளை தொடர்புகளின் ஒரு வகைப்பாடாகவும் கொள்ளலாம்:

X லிருந்து Y கணத்திற்கு வரையறுக்கப்படும் தொடர்பு என்பது (x, y) வரிசைச் சோடிகளைக் கொண்ட கணம். இவ்வரிசைச் சோடிகளில், ${\displaystyle x\in X}$ மற்றும் ${\displaystyle y\in Y}$.

இடது-முழுமை மற்றும் வலது-தனித்த என அமையும் சிறப்புத் தொடர்பாக ஒரு சார்பைக் கருதலாம். X மற்றும் Y கணங்கள் குறிப்பிடப்படாமல் இருந்தால் சார்புகளைத் தொடர்பின் ஒரு வகையாகக் கருதுவது இயலாது.

f : X → Y என்ற குறியீடு X -ஐ ஆட்களமாகவும் Y -ஐ இணையாட்களமாகவும் கொண்ட சார்பு f என்பதைக் குறிக்கிறது. அனைத்து y -களால் அமைந்த கணம் சார்பின் எதிருரு அல்லது வீச்சு எனப்படும். வீச்சு எல்லா சார்புகளிலும் அவற்றின் இணையாட்களத்திற்குச் சமமாக இருக்க வேண்டியதில்லை.

சார்பின் உள்ளீடு சார்பின் மாறி எனவும் அந்த உள்ளீட்டிற்குரிய வெளியீடு சார்பின் மதிப்பு அல்லது அவ்வுள்ளீட்டின் எதிருரு எனவும் அழைக்கப்படும். ஆட்களத்தில் உள்ள ஒரு உறுப்பு x எனில் அதனோடு இணைக்கப்படும் இணையாட்களத்தின் தனித்த உறுப்பு y என்பது x -ன் எதிருரு அல்லது, x -ன் சார்பு மதிப்பு எனப்படும். ƒ -ன் கீழ் இணைக்கப்படும் x -ன் எதிருரு ƒ(x) எனக் குறிக்கப்படும்.

ஒரு சார்பின் வரைபடம் என்பது அச்சார்பின் வரிசைச் சோடிகளை ஆள்கூறுகளாகக் கொண்ட புள்ளிகளைக் கார்ட்டீசியன் தளத்தில் குறிப்பதால் கிடைக்கும் வரைபடமாகும்.

ஆட்களம் X வெற்றுக்கணமாக இருக்கலாம். X = ∅ எனில் F = ∅. இணையாட்களம் Y = ∅ எனில் X = ∅ மற்றும் F = ∅. இத்தைகைய வெற்றுச்சார்புகள் பொதுவாக காணப்படுவதில்லை என்றாலும் கொள்கையளவில் அவை உள்ளதாகக் எடுத்துக்கொள்ளப்படுன்றன.

குறியீடு

ஒரு சார்பின் முறையான விளக்கமானது அச்சார்பின் பெயர், ஆட்களம், இணையாட்களம் மற்றும் இணைக்கும் விதி ஆகியவற்றைக் கொண்டிருக்கும். கீழே தரப்பட்டுள்ள குறியீடு இரு பகுதிகளைக் கொண்டுள்ளது:

• ${\displaystyle {\begin{aligned}f\colon \mathbf {N} &\to \mathbf {R} \\n&\mapsto {\frac {n}{\pi }}\end{aligned}}}$

முதல் பகுதி,

"ƒ என்பது N லிருந்து R -க்கு வரையறுக்கப்பட்ட ஒரு சார்பு" என்பதையும்

இரண்டாவது பகுதி,

"${\displaystyle n,\,}$ ${\displaystyle {\frac {n}{\pi }}.\,\!}$ -உடன் இணைக்கப்படுகிறது" என்பதையும் குறிக்கின்றன.

இச்சார்பின் ஆட்களம் இயல் எண் கணம், இணையாட்களம் மெய்யெண்கணம். இச்சார்பு n -ஐ அதனை π -ஆல் வகுக்கப்பட்ட கணியத்துடன் இணைக்கிறது.

இதனைச் சுருக்கமாக:

${\displaystyle f(n)={\frac {n}{\pi }},\,\!}$ என எழுதலாம்.

f(n), "f ஆஃப் (of) n" என வாசிக்கப்படுகிறது. ஆனால் இவ்வாறு சுருக்கமாக எழுதும்போது ஆட்களமும்(N) இணையாட்களமும் (R) வெளிப்படையாகக் குறிக்கப்படுவதில்லை.

சார்பின் வகைகள்

• உள்ளிடு சார்பு
• முழுச் சார்பு
• இருவழிச் சார்பு
• பல மாறிச் சார்பு
• இரு சார்புகளின் தொகுப்பு சார்பு
• முற்றொருமைச் சார்பு
• நேர்மாறுச் சார்பு

சார்பு வெளிகள்

X கணத்திலிருந்து Y கணத்திற்கு வரையறுக்கப்பட்ட அனைத்து சார்புகளையும் கொண்ட கணம் சார்பு வெளி எனப்படுகிறது.

இதன் குறியீடு:

[X → Y], அல்லது Y^X.

ஆட்களத்தின் அளவை எண் |X|;

இணை ஆட்களத்தின் அளவை எண் |Y|

• இவை இரண்டும் முடிவுறு எண்கள் எனில், X லிருந்து Y -க்கு வரையறுக்கப்படும் சார்புகளின் எண்ணிக்கை:

|Y^X| = |Y|^|X|.

• |X| முடிவுறா எண்ணாகவும் Y கணம் ஒன்றுக்கு மேற்பட்ட உறுப்புகளோடும் இருந்தால், X லிருந்து Y -க்கு வரையறுக்கப்படும் சார்புகள் எண்ணுறா அளவிலானவை. எனினும் அவற்றில் எண்ணக்கூடிய அளவிலான சார்புகள் மட்டுமே ஒரு வாய்ப்பாடாக எழுதக் கூடியவையாக இருக்கும்.

சார்பு, ƒ: X → Y எனில் ƒ ∈ [X → Y] என்பது தெளிவு.