செங்கோண முக்கோணம்

வடிவவியலில் ஒரு முக்கோணத்தின் ஒரு கோணம் செங்கோணம் (அதாவது 90°) எனில் அம்முக்கோணம் செங்கோண முக்கோணம் (right triangle அல்லது right-angled triangle) என அழைக்கப்படும். செங்கோண முக்கோணத்தின் பக்கங்களுக்கும் கோணங்களுக்கும் இடையேயுள்ள தொடர்புதான் முக்கோணவியலின் அடிப்படையாக அமைகிறது.

செங்கோண முக்கோணம்

சொல்லியல்

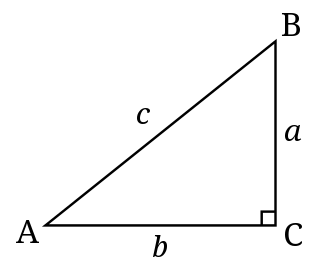
ஒரு செங்கோண முக்கோணத்தில் செங்கோணத்திற்கு எதிரில் உள்ள பக்கம் செம்பக்கம் (hypotenuse) எனவும், செங்கோணத்தைத் தாங்கும் இரு பக்கங்களும் தாங்கிப் பக்கங்கள் (catheti -plural; cathetus -singular) எனவும் அழைக்கப்படுகின்றன . படத்தில் செம்பக்கம் a. பக்கம் a, B கோணத்திற்கு அடுத்தள்ள பக்கமாகவும், A கோணத்திற்கு எதிர்ப்பக்கமாகவும் உள்ளது. பக்கம் b, A கோணத்திற்கு அடுத்துள்ள பக்கமாகவும், B கோணத்திற்கு எதிர்ப்பக்கமாகவும் அமைகிறது.

மூன்று பக்க அளவுகளும் முழு எண்களாக இருந்தால் அச்செங்கோண முக்கோணம் பித்தாகரசு முக்கோணம் எனப்படும். அம்மூன்று பக்க அளவுகளும் பித்தாகரசின் மும்மை எனப்படும்

முதன்மைப் பண்புகள்

பரப்பு

ஏனைய முக்கோணங்களுக்குப் போலவே செங்கோண முக்கோணத்தின் பரப்பு, அதன் அடிப்பக்கம் மற்றும் அந்த அடிப்பக்கத்தின் குத்துயரம் இரண்டின் பெருக்குத்தொகையில் பாதியாகும். செங்கோண முக்கோணத்தில் ஒரு தாங்கிப் பக்கத்தை அடிப்பக்கமாக எடுத்துக் கொண்டால் மற்றொரு தாங்கிப் பக்கம் குத்துயரமாக இருக்கும்.

பரப்பு T -ன் வாய்ப்பாடு:

${\displaystyle T={\tfrac {1}{2}}ab}$

இங்கு a மற்றும் b இரண்டும் தாங்கிப் பக்கங்கள்.

செங்கோண முக்கோணத்தின் உள்வட்டமானது செம்பக்கம் AB -ஐ புள்ளி P -ல் தொடுகிறது எனில்,

${\displaystyle PA=s-a\,}$

${\displaystyle PB=s-b\,}$

பரப்பு T:

${\displaystyle T={\text{PA}}\cdot {\text{PB}}=(s-a)(s-b).}$

குத்துயரம்

செங்கோண முக்கோணத்தின் குத்துயரம்.

செங்கோணத்தைக் கொண்ட உச்சியிலிருந்து செம்பக்கத்துக்கு வரையப்படும் குத்துயரம் செங்கோண முக்கோணத்தை இரண்டு சிறிய செங்கோண முக்கோணங்களாகப் பிரிக்கும். இவ்விரண்டும் ஒன்றுக்கொன்று வடிவொத்தவையாகவும் மூல முக்கோணத்திற்கும் வடிவொத்தவையாகவும் இருக்கும்.

எனவே:

இக்குத்துயரம் செம்பக்கத்தின் இரு கோட்டுத்துண்டுகளின் பெருக்கல் சராசரியாக (இடை விகிதசமன்) அமையும்.

${\displaystyle \displaystyle f^{2}=de,}$ (சில நேரங்களில் இம்முடிவானது செங்கோண முக்கோணக் குத்துயரத் தேற்றம் என்றும் அழைக்கப்படுகிறது.)

தாங்கிப் பக்கங்கள் ஒவ்வொன்றும் செம்பக்கம் மற்றும் அத்தாங்கிப் பக்கத்தை அடுத்துள்ள செம்பக்க கோட்டுத்துண்டு இரண்டின் இடை விகிதசமனாக இருக்கும்.

அதாவது:

${\displaystyle \displaystyle b^{2}=ce,}$

${\displaystyle \displaystyle a^{2}=cd}$

இங்கு a, b, c, d, e, f என்பவை படத்தில் காட்டப்பட்டுள்ளவாறு அமையும்.^[1]

இவ்விரண்டு முடிவுகளிலிலிருந்து:

${\displaystyle f={\frac {ab}{c}}.}$

மேலும் செம்பக்கத்திற்கு வரையப்படும் குத்துயரமானது செங்கோணத்தைத் தாங்கும் பக்கங்களோடு பின்வருமாறு தொடர்பு கொண்டுள்ளது.^[2][3]

${\displaystyle {\frac {1}{a^{2}}}+{\frac {1}{b^{2}}}={\frac {1}{f^{2}}}.}$

பித்தாகரசு தேற்றம்

பித்தாகரசு தேற்றத்தின் கூற்று:

எந்தவொரு செங்கோண முக்கோணத்திலும் செம்பக்கத்தின் மீது வரையப்படும் சதுரத்தின் பரப்பு, தாங்கிப் பக்கங்களின் மீது வரையப்படும் சதுரங்களின் பரப்புகளின் கூடுதலுக்குச் சமம்.

இதன் சமன்பாடு வடிவம்:

${\displaystyle c^{2}=a^{2}+b^{2}\,}$

தேவையானதும் போதுமானதுமான கட்டுப்பாடுகள்

முக்கோணம் ABC இன் பக்கங்கள் ${\displaystyle a\leq b<c}$, அரைச்சுற்றளவு s, பரப்பளவு T, மிகநீளமான பக்கத்தின் செங்குத்துயரம் h , சுற்றுவட்ட ஆரம் R, உள்வட்ட ஆரம் r, வெளிவட்ட ஆரங்கள் r_a, r_b, r_c , நடுக்கோடுகளின் நீளங்கள் m_a, m_b, m_c எனில் கீழுள்ள ஆறுவகைகளிலுள்ள எவையேனும் ஒரு முடிவு உண்மையாக இருந்தால், இருந்தால் மட்டுமே, அம்முக்கோணம் செங்கோண முக்கோணம் ஆகும். இம்முடிவுகள் அனைத்துமே ஒரு செங்கோண முக்கோணத்தின் பண்புகள் ஆகும்.

பக்கங்களும் அரைச்சுற்றளவும்

• ${\displaystyle \displaystyle a^{2}+b^{2}=c^{2}\quad ({\text{Pythagorean theorem}})}$
• ${\displaystyle \displaystyle (s-a)(s-b)=s(s-c)}$
• ${\displaystyle \displaystyle s=2R+r.}$^[4]
• ${\displaystyle \displaystyle a^{2}+b^{2}+c^{2}=8R^{2}.}$^[5]

கோணங்கள்

• A , B கோணங்கள் இரண்டும் [[நிரப்புக் கோணங்கள்^[6]
• ${\displaystyle \displaystyle \cos {A}\cos {B}\cos {C}=0.}$^[5][7]
• ${\displaystyle \displaystyle \sin ^{2}{A}+\sin ^{2}{B}+\sin ^{2}{C}=2.}$^[5][7]
• ${\displaystyle \displaystyle \cos ^{2}{A}+\cos ^{2}{B}+\cos ^{2}{C}=1.}$^[7]
• ${\displaystyle \displaystyle \sin {2A}=\sin {2B}=2\sin {A}\sin {B}.}$

பரப்பளவு

• ${\displaystyle \displaystyle T={\frac {ab}{2}}}$
• ${\displaystyle \displaystyle T=r_{a}r_{b}=rr_{c}}$
• ${\displaystyle \displaystyle T=r(2R+r)}$
• ${\displaystyle T=PA\cdot PB,}$ மிக நீளமான பக்கம் AB ஐ உள்வட்டம் தொடும்புள்ளி P ^[8]

உள்வட்ட ஆரமும் வெளிவட்ட ஆரங்களும்^[9]

• ${\displaystyle \displaystyle r=s-c=(a+b-c)/2}$
• ${\displaystyle \displaystyle r_{a}=s-b=(a-b+c)/2}$
• ${\displaystyle \displaystyle r_{b}=s-a=(-a+b+c)/2}$
• ${\displaystyle \displaystyle r_{c}=s=(a+b+c)/2}$
• ${\displaystyle \displaystyle r_{a}+r_{b}+r_{c}+r=a+b+c}$
• ${\displaystyle \displaystyle r_{a}^{2}+r_{b}^{2}+r_{c}^{2}+r^{2}=a^{2}+b^{2}+c^{2}}$
• ${\displaystyle \displaystyle r={\frac {r_{a}r_{b}}{r_{c}}}}$

குத்துயரங்களும் நடுக்கோடுகளும்

• ${\displaystyle \displaystyle h={\frac {ab}{c}}}$
• ${\displaystyle \displaystyle m_{a}^{2}+m_{b}^{2}+m_{c}^{2}=6R^{2}.}$^[10]
• ஒரு நடுக்கோட்டின் நீளம், சுற்றுவட்ட ஆரத்திற்குச் சமம்.
• குத்துயரங்களிலேயே சிறிய குத்துயரமானது, அதற்கு எதிர்ப்பக்கத்தைப் பிரிக்கும் கோட்டுத்துண்டுகளின் நீளங்களின் பெருக்கல் சராசரியாக இருக்கும் (செங்கோண முக்கோணக் குத்துயரத் தேற்றம்).

சுற்றுவட்டமும் உள்வட்டமும்

• முக்கோணத்தின் ஒரு பக்கம் விட்டத்துடன் ஒன்றுமாறு முக்கோணத்தை ஒரு அரைவட்டத்துக்குள் வரையலாம் (தேலேசுத் தேற்றம்).
• சுற்றுவட்ட மையம் முக்கோணத்தின் மிகநீளப் பக்கத்தின் நடுப்புள்ளியாக இருக்கும்.
• முக்கோணத்தின் மிகநீளமான பக்கம் சுற்றுவட்டத்தின் விட்டமாகும்.${\displaystyle \displaystyle (c=2R).}$
• சுற்றுவட்டத்தை, ஒன்பது-புள்ளி வட்டத்தைத் தொடும்.^[5]
• செங்கோட்டுச்சந்தி சுற்றுவட்டத்தின் மீதமையும்.^[10]
• உள்வட்ட மையத்திற்கும் செங்கோட்டுச்சந்திக்கும் இடைப்பட்ட தூரம் ${\displaystyle {\sqrt {2}}r}$.^[10]

முக்கோணவியல் விகிதங்கள்

ஒரு செங்கோண முக்கோணத்தின் பக்கங்களின் விகிதங்களைப் பயன்படுத்தி குறுங்கோணங்களுக்கான முக்கோணவியல் சார்புகளை வரையறுக்கலாம்.

செங்கோண முக்கோணம்.

வடிவொத்த முக்கோணங்களின் ஒத்தபக்கங்களின் விகிதங்கள் சமமாக இருக்கும் என்ற உண்மையிலிருந்து, ஒரு முக்கோணத்தின் பக்க நீளங்களுக்கும் கோண அளவுகளுக்கும் தொடர்பு இருக்கும் என்ற கருத்து அறியப்படுகிறது. இரு செங்கோண முக்கோணங்களில் ஒன்றின் செம்பக்கம் மற்றதன் செம்பக்க நீளத்தைப் போல இருமடங்கு எனில் மற்ற பக்கங்களும் அவ்வாறே அமையும். இந்த பக்க விகிதங்களைத்தான் முக்கோணவியல் சார்புகள் தருகின்றன.

ஒரு செங்கோண முக்கோணத்தின் கோணம் A -ன் முக்கோணவியல் சார்புகளை வரையறுக்க அம்முக்கோணத்தின் பக்கங்களைப் பின்வருமாறு அழைக்கலாம்:

• செம்பக்கம் (அல்லது கர்ணம்) (hypotenuse):

செங்கோணத்திற்கு எதிர்ப்பக்கம். இதன் அளவு  h. ஒரு செங்கோண முக்கோணத்தில் செம்பக்கந்தான் மூன்று பக்கங்களிலும் நீளமானது.

• எதிர்ப்பக்கம் (opposite):

நாம் எடுத்துக்கொண்ட கோணம் A -க்கு எதிரில் அமையும் பக்கம். இதன் நீளம்  a.

• அடுத்துள்ள பக்கம் (adjacent):

செங்கோணம் மற்றும் நாம் எடுத்துக்கொண்ட கோணம் இரண்டிற்கும் ( A மற்றும் C) பொதுவான பக்கம். இதன் நீளம்  b.

முக்கோணவியல் சார்புகள்:

${\displaystyle \sin A={\frac {\textrm {opposite}}{\textrm {hypotenuse}}}={\frac {a}{h}}.}$

${\displaystyle \cos A={\frac {\textrm {adjacent}}{\textrm {hypotenuse}}}={\frac {b}{h}}.}$

${\displaystyle \tan A={\frac {\textrm {opposite}}{\textrm {adjacent}}}={\frac {a}{b}}.}$

${\displaystyle \csc A={\frac {1}{\sin A}}={\frac {\textrm {hypotenuse}}{\textrm {opposite}}}={\frac {h}{a}}.}$

${\displaystyle \sec A={\frac {1}{\cos A}}={\frac {\textrm {hypotenuse}}{\textrm {adjacent}}}={\frac {h}{b}}.}$

${\displaystyle \cot A={\frac {1}{\tan A}}={\frac {\textrm {adjacent}}{\textrm {opposite}}}={\frac {b}{a}}.}$

சிறப்புவகை செங்கோண முக்கோணங்கள்

சிறப்புக் கோணங்களைக் கொண்ட செங்கோண முக்கோணங்களைப் பயன்படுத்தி சில குறிப்பிட்ட கோணங்களுக்கான முக்கோணவியல் சார்புகளின் மதிப்புகளைக் காணலாம்.

30-60-90 முக்கோணத்திலிருந்து π/6 -ன் மடங்காக அமையும் கோணங்களின் முக்கோணவியல் சார்புகளின் மதிப்புகளையும்;

45-45-90 முக்கோணத்திலிருந்து π/4 -ன் மடங்காக அமையும் கோணங்களின் முக்கோணவியல் சார்புகளின் மதிப்புகளையும் காண முடியும்.

தேலேசுத் தேற்றம்

செங்கோண முக்கோணத்தில் செங்கோணத்தின் நடுக்கோடு

தேலேசுத் தேற்றக் கூற்றின்படி:

BC -ஐ விட்டமாகக் கொண்ட வட்டத்தின் மீது அமைந்த ஏதேனுமொரு புள்ளி A எனில், ( B அல்லது C -தவிர) △ABC ஒரு செங்கோண முக்கோணமாகும். செங்கோணம் உச்சி A -ல் அமையும்.

மறுதலைக் கூற்று:

ஒரு வட்டத்துக்குள் செங்கோண முக்கோணம் ஒன்று வரையப்பட்டால் அதன் செம்பக்கம் வட்டத்தின் விட்டமாகும்.

கிளை முடிவு:

• செம்பக்கத்தின் நீளம், செங்கோண உச்சிக்கும் செம்பக்கத்தின் நடுப்புள்ளிக்கும் இடையேயுள்ள தூரத்தைப் போல இருமடங்காகும்.

• மேலும் இந்த செங்கோண முக்கோணத்தின் சுற்றுவட்டத்தின் மையம் செம்பக்கத்தின் நடுப்புள்ளியாகவும் ஆரம் செம்பக்கத்தின் நீளத்தில் பாதியாகவும் அமையும்.

நடுக்கோடுகள்

ஒரு செங்கோண முக்கோணத்தின் நடுக்கோடுகளுக்கு பின்வரும் முடிவு உண்மையாக இருக்கும்:

${\displaystyle m_{a}^{2}+m_{b}^{2}=5m_{c}^{2}={\frac {5}{4}}c^{2}.}$

செம்பக்கத்திற்கு வரையப்படும் நடுக்கோடு, மூல செங்கோண முக்கோணத்தை இரண்டு இருசமபக்க முக்கோணங்களாகப் பிரிக்கும்.

சராசரிகளுடன் தொடர்பு

H, G மற்றும் A என்பவை முறையே a , b ( a > b) என்ற இரு நேர்ம எண்களின் இசைச் சராசரி, பெருக்கல் சராசரி மற்றும் கூட்டுச் சராசரி என்க.

ஒரு செங்கோண முக்கோணம் H , G -ஐ தாங்கிப் பக்கங்களாகவும்a A -ஐ செம்பக்கமாகவும் கொண்டிருந்தால், ^[11]

${\displaystyle {\frac {A}{H}}={\frac {A^{2}}{G^{2}}}={\frac {G^{2}}{H^{2}}}=\phi \,}$

மற்றும்

${\displaystyle {\frac {a}{b}}=\phi ^{3},\,}$

இங்கு ${\displaystyle \phi ,}$ என்பது தங்க விகிதம் ${\displaystyle {\tfrac {1+{\sqrt {5}}}{2}}.\,}$ ஆகும்.

ஏனைய பண்புகள்

a, b -தாங்கிப் பக்கங்களாகவும் c -செம்பக்கமாகவும் கொண்ட செங்கோண முக்கோணத்தின் உள்வட்ட ஆரம்:

${\displaystyle r={\frac {a+b-c}{2}}={\frac {ab}{a+b+c}}.}$

p, q நீளமுள்ள கோட்டுத்துண்டுகள் உச்சி C லிருந்து செம்பக்கத்தை c/3 நீளமுள்ள மூன்று சமதுண்டுகளாகப் பிரித்தால்: ^{[12]:pp. 216-217}

${\displaystyle p^{2}+q^{2}=5\left({\frac {c}{3}}\right)^{2}.}$

முக்கோணத்துக்குள் வெவ்வேறான இரண்டு சதுரங்கள் வரையக்கூடிய முக்கோணங்கள் செங்கோண முக்கோணங்கள் மட்டும்தான் ^[13]

அவ்வாறு ஒரு செங்கோண முக்கோணத்துக்குள் வரையப்பட்ட வெவ்வேறு இரு சதுரங்களின் பக்க நீளங்கள் h, s (h>s). செம்பக்கம் c எனில்:

${\displaystyle {\frac {1}{c^{2}}}+{\frac {1}{h^{2}}}={\frac {1}{s^{2}}}.}$