Стискна теорема

Стискна теорема (теорема про двох поліцейських, англ. squeeze theorem) — теорема в математичному аналізі про границю функції, яка «затиснута» між двома іншими функціями, що мають рівні границі.

Візуалізація теореми про стиснення для функцій ${\displaystyle {\color {OliveGreen}g(x)=x^{2}}}$, ${\displaystyle {\color {Blue}f(x)=x^{2}\sin {\frac {1}{x}}}}$ та ${\displaystyle {\color {Orange}h(x)=-x^{2}}}$ при ${\displaystyle x\to 0}$

Теорема про стиснення також відома під назвами як теорема про двох поліцейських, теорема про двох карабінерів і теорема про двох жандармів. Інтерпретація полягає в тому, що якщо двоє поліцейських супроводжують п’яного ув’язненого між собою, і обидва офіцери йдуть до камери, то незалежно від того як коливається ув’язнений, він все одно опиниться в камері.

Формулювання

Нехай ${\displaystyle A\subset \mathbb {R} }$, ${\displaystyle x_{0}}$ — гранична точка множини ${\displaystyle A}$, функції f, g і h визначені на ${\displaystyle A}$, для яких виконуються наступні умови: ${\displaystyle g(x)\leqslant f(x)\leqslant h(x)}$ для всіх ${\displaystyle x\in A}$; ${\displaystyle \lim _{x\to x_{0}}g(x)=\lim _{x\to x_{0}}h(x)=a}$. Тоді ${\displaystyle \lim _{x\to x_{0}}f(x)=a.}$

• Функції g і h називають верхньою та нижньою межами f відповідно.
• Тут ${\displaystyle x_{0}}$ не мусить бути внутрішньою точкою множини ${\displaystyle A}$.
• Схоже твердження справедливе і при ${\displaystyle x\to +\infty }$ або ${\displaystyle x\to -\infty }$.

Доведення

Проведемо доведення із використанням означення границі функції в точці за Коші, тобто нам потрібно довести, що для кожного дійсного ${\displaystyle \varepsilon >0}$ існує дійсне ${\displaystyle \delta >0}$ таке, що для всіх ${\displaystyle x\in A\cap (x_{0}-\delta ,x_{0}+\delta )\setminus \{x_{0}\}}$ виконується ${\displaystyle |f(x)-a|<\varepsilon }$. Тобто,

${\displaystyle \forall \varepsilon >0\ \exists \,\delta >0:\forall x\in A\cap (x_{0}-\delta ,x_{0}+\delta )\setminus \{x_{0}\}\ |f(x)-a|<\varepsilon .}$.

З того, що

${\displaystyle \lim _{x\to x_{0}}g(x)=a}$

випливає, що

$${\displaystyle \forall \varepsilon >0\,\exists \,\delta _{1}>0:\forall x\in A\cap (x_{0}-\delta _{1},x_{0}+\delta _{1})\setminus \{x_{0}\}\,|g(x)-a|<\varepsilon }$$

(1)

і з того, що

${\displaystyle \lim _{x\to x_{0}}h(x)=a}$

випливає, що

$${\displaystyle \forall \varepsilon >0\ \exists \,\delta _{2}>0:\forall x\in A\cap (x_{0}-\delta _{2},x_{0}+\delta _{2})\setminus \{x_{0}\}\,|h(x)-a|<\varepsilon .}$$

(2)

Також маємо, що

${\displaystyle g(x)\leqslant f(x)\leqslant h(x)}$,

звідси

${\displaystyle g(x)-a\leqslant f(x)-a\leqslant h(x)-a}$ ${\displaystyle \forall x\in A}$.

Покладемо ${\displaystyle \delta$ :=\min\{\delta _{1},\delta _{2}\}} . Тоді, для всіх ${\displaystyle x\in A\cap (x_{0}-\delta ,x_{0}+\delta )\setminus \{x_{0}\}}$, поєднавши (1) та (2), отримаємо

${\displaystyle -\varepsilon <g(x)-a\leqslant f(x)-a\leqslant h(x)-a<\varepsilon ,}$

${\displaystyle -\varepsilon <f(x)-a<\varepsilon ,}$

що й треба було довести.

Приклад

Перший приклад

x² sin(1/x) затиснута як x прямує до 0

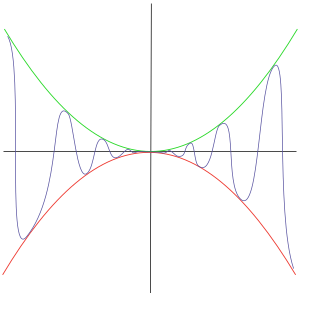
Границю

${\displaystyle \lim _{x\to 0}x^{2}\sin({\tfrac {1}{x}})}$

неможливо встановити через закон

${\displaystyle \lim _{x\to a}(f(x)\cdot g(x))=\lim _{x\to a}f(x)\cdot \lim _{x\to a}g(x),}$

бо

${\displaystyle \lim _{x\to 0}\sin({\tfrac {1}{x}})}$

не існує.

Однак, з визначення синуса,

${\displaystyle -1\leq \sin({\tfrac {1}{x}})\leq 1.\,}$

Випливає, що

${\displaystyle -x^{2}\leq x^{2}\sin({\tfrac {1}{x}})\leq x^{2}\,}$

З того, що ${\displaystyle \lim _{x\to 0}-x^{2}=\lim _{x\to 0}x^{2}=0}$, за стискною теоремою, ${\displaystyle \lim _{x\to 0}x^{2}\sin({\tfrac {1}{x}})}$ повинен бути 0.

Другий приклад

Порівняння площ:
${\displaystyle {\begin{aligned}&\,A(\triangle ADF)\geqslant A({\text{сектор}}\,ADB)\geqslant A(\triangle ADB)\\\Rightarrow &\,{\frac {1}{2}}\cdot {\text{tg}}\,x\cdot 1\geqslant {\frac {x}{2\pi }}\cdot \pi \geq {\frac {1}{2}}\cdot \sin x\cdot 1\\\Rightarrow &\,{\frac {\sin x}{\cos x}}\geqslant x\geqslant \sin x\\\Rightarrow &\,{\frac {\cos x}{\sin x}}\leqslant {\frac {1}{x}}\leqslant {\frac {1}{\sin x}}\\\Rightarrow &\,\cos x\leqslant {\frac {\sin x}{x}}\leqslant 1\end{aligned}}}$

Напевно найвідоміші приклади знаходження границь через теорему затискання — це доведення того, що

${\displaystyle {\begin{aligned}&\lim _{x\to 0}{\frac {\sin x}{x}}=1,\\[10pt]&\lim _{x\to 0}{\frac {1-\cos x}{x}}=0.\end{aligned}}}$

Перша границя випливає з використання стискної теореми і того факту, що

${\displaystyle \cos x\leqslant {\frac {\sin x}{x}}\leqslant 1}$

для x досить близького, але не рівного 0. Правильність якого для додатного x можна побачити за допомогою геометричних міркувань (див. рисунок), які також можна поширити на від’ємне x. Часто цю границю називають першою чудовою границею.

Друга випливає з теореми стиснення і того факту, що

${\displaystyle 0\leqslant {\frac {1-\cos x}{x}}\leqslant x}$

для x досить близького, але не рівного 0. Це можна отримати, замінивши ${\displaystyle \sin x}$ у попередньому факті на ${\displaystyle {\sqrt {1-\cos ^{2}x}}}$ і піднісши отриману нерівність до квадрату.

Ці дві границі використовуються для доведення того, що похідна синуса є косинус. На це спираються виведення похідних для інших тригонометричних функцій.

Третій приклад

Можна показати, що

${\displaystyle ({\text{tg}}\,\theta )^{\prime }={\frac {1}{\cos ^{2}\theta }}=\sec ^{2}\theta .}$

На рисунку площа меншого з двох заштрихованих секторів круга дорівнює

${\displaystyle {\frac {\Delta \theta \sec ^{2}\theta }{2}}={\frac {\Delta \theta }{2\cos ^{2}\theta }}}$

оскільки радіус дорівнює ${\displaystyle {\frac {1}{\cos \theta }}}$, а дуга на одиничному колі має довжину Δθ. Аналогічно, площа більшого з двох заштрихованих секторів дорівнює

${\displaystyle {\frac {\Delta \theta \sec ^{2}(\theta +\Delta \theta )}{2}}={\frac {\Delta \theta }{2\cos ^{2}(\theta +\Delta \theta )}}.}$

Між секторами стиснутий трикутник, основою якого є вертикальний відрізок, який сполучає дві виділені на рисунку точки. Довжина основи трикутника дорівнює ${\displaystyle {\text{tg}}\,(\theta +\Delta \theta )-{\text{tg}}\,\theta }$, а висота — ${\displaystyle -1}$. Отже, площа трикутника дорівнює

${\displaystyle {\frac {{\text{tg}}\,(\theta +\Delta \theta )-{\text{tg}}\,\theta }{2}}.}$

З нерівностей

${\displaystyle {\frac {\Delta \theta }{2\cos ^{2}\theta }}\leqslant {\frac {{\text{tg}}\,(\theta +\Delta \theta )-{\text{tg}}\,\theta }{2}}\leqslant {\frac {\Delta \theta }{2\cos ^{2}(\theta +\Delta \theta )}}}$

випливає

${\displaystyle {\frac {1}{\cos ^{2}\theta }}\leqslant {\frac {{\text{tg}}(\theta +\Delta \theta )-{\text{tg}}\,\theta }{\Delta \theta }}\leqslant {\frac {1}{\cos ^{2}(\theta +\Delta \theta )}}}$

за умови Δθ > 0, а якщо Δθ < 0, то нерівність перевертається. Оскільки перший і третій вирази прямують до ${\displaystyle {\frac {1}{\cos ^{2}\theta }}}$ при ${\displaystyle \Delta \theta \to 0}$, а середній вираз прямує до ${\displaystyle ({\text{tg}}\,\theta )^{\prime }}$, то це дає бажаний результат.

Четвертий приклад

Стискна теорема також може використовуватися в багатовимірному аналізі. У цьому випадку функції g та h повинні обмежувати f в околі точки, що цікавить, і вона працює, лише тоді якщо функція f дійсно там має границю. Таким чином, у багатовимірному випадку цю теорему можна використовувати, щоб довести, що функція f має границю в точці, але її не можна використовувати, щоб довести відсутність границі в точці.

${\displaystyle \lim _{(x,y)\to (0,0)}{\frac {x^{2}y}{x^{2}+y^{2}}}}$

не можна знайти, взявши будь-які границі уздовж кривих, які проходять через точку ${\displaystyle (0,0)}$, але оскільки

${\displaystyle 0\leqslant {\frac {x^{2}}{x^{2}+y^{2}}}\leqslant 1}$,

${\displaystyle -\left|y\right\vert \leqslant y\leqslant \left|y\right\vert }$,

${\displaystyle -\left|y\right\vert \leqslant {\frac {x^{2}y}{x^{2}+y^{2}}}\leqslant \left|y\right\vert }$,

${\displaystyle \lim _{(x,y)\to (0,0)}-\left|y\right\vert =0}$,

${\displaystyle \lim _{(x,y)\to (0,0)}\left|y\right\vert =0}$,

${\displaystyle 0\leqslant \lim _{(x,y)\to (0,0)}{\frac {x^{2}y}{x^{2}+y^{2}}}\leqslant 0}$,

то за стискною теоремою

${\displaystyle \lim _{(x,y)\to (0,0)}{\frac {x^{2}y}{x^{2}+y^{2}}}=0}$.

Теорема про три послідовності

Коли послідовність лежить між двома іншими збіжними послідовностями з такою ж границею, то вона також сходить до цієї границі

Стискна теорема також справедлива для послідовностей як функцій цілого аргументу:

Нехай для послідовностей ${\displaystyle \{a_{n}\}_{n=1}^{+\infty }}$, ${\displaystyle \{b_{n}\}_{n=1}^{+\infty }}$ і ${\displaystyle \{c_{n}\}_{n=1}^{+\infty }}$ виконуються наступні умови: ${\displaystyle \forall n\geqslant 1\,a_{n}\leqslant b_{n}\leqslant c_{n}}$; ${\displaystyle \lim _{n\to \infty }a_{n}=\lim _{n\to \infty }c_{n}=l}$. Тоді ${\displaystyle \lim _{n\to \infty }b_{n}=l}$.

У цьому випадку її часто називають теоремою про три послідовності. Доведення схоже як і для функцій дійсного аргументу.

Доведення

Нехай ${\displaystyle \varepsilon >0}$ задане. Згідно з умови теореми

${\displaystyle \exists n_{1}\in \mathbb {N}$ :\,\forall n\geqslant n_{1}\,\,l-\varepsilon <a_{n}} ,

${\displaystyle \exists n_{2}\in \mathbb {N}$ :\,\forall n\geqslant n_{2}\,\,c_{n}<l+\varepsilon } .

Тоді для всіх ${\displaystyle n\geqslant n_{0}:=\max\{n_{1},n_{2}\}}$ маємо:

${\displaystyle l-\varepsilon <a_{n}\leqslant b_{n}\leqslant c_{n}<l+\varepsilon }$,

звідки випливає, що

${\displaystyle l-\varepsilon <b_{n}<l+\varepsilon }$,

що і треба було довести.

Джерела

• Григорій Михайлович Фіхтенгольц. Курс диференціального та інтегрального числення. — 2025. — 2391 с.(укр.)
• Банах С. Курс функціонального аналізу (лінійні операції). — К. : Радянська школа, 1948. — 216 с.(укр.)
• Банах С. Диференціальне та інтегральне числення = Rachunek różniczkowy i całkowy. — 2-е. — М. : Наука, 1966. — 436 с.(рос.)
• Березанський Ю. М., Ус Г. Ф., Шефтель З. Г. Функціональний аналіз : [укр.] = Functional Analysis, Vol. I, Kyiv : Institute of Mathematics, 2010. : [пер. з англ.] : підручник. — Л. : Видавець Чижиков І. Е., 2014. — С. 559. — (Університетська бібліотека). — ISBN 978-966-2645-12-5.
• Ляшко І.І., Ємельянов В.Ф., Боярчук О.К. Математичний аналіз. Частина 1. — К. : Вища школа, 1992. — 496 с. — ISBN 5-11-003757-4.(укр.)
• Дороговцев А. Я. Математичний аналіз. Частина 1. — К. : Либідь, 1993. — 320 с. — ISBN 5-325-00380-1.(укр.)
• Weisstein, Eric W. Стискна теорема(англ.) на сайті Wolfram MathWorld.