Синус

У Вікіпедії є статті про інші значення цього терміна: Синус (значення).

Синус (лат. sinus — «пазуха») — тригонометрична функція кута. Визначення синусу гострого кута в контексті прямокутного трикутника: для заданого кута, є відношенням довжини катета, що є протилежним даному куту, до довжини найдовшої сторони трикутника (гіпотенузи).

У загальнішому випадку, визначення синуса (та інших тригонометричних функцій) може бути розширене до значення дійсного числа, що належить до довжини певного відрізка в одиничному колі. Більш складні сучасні визначення задають синус як нескінченний ряд або як розв'язок деяких диференційних рівнянь, що дозволяє їх розширення до довільних додатних і від'ємних значень і навіть до комплексних чисел.

Функція синуса зазвичай застосовується в моделюванні періодичних явищ, таких як звукові і світлові хвилі, позиції і швидкості гармонічних коливань, інтенсивності сонячного світла і довжини для, коливань середньої температури в період року.

Функція синус має зв'язок у своєму походженні до функцій джа і коті-джа, що використовувалися в період Гупта в Індійській астрономії (Ар'ябхатія, Сур'я Сіддханта), шляхом перекладу із санскриту на арабську мову, а потім з арабської на латинь^[1]. Слово «синус» походить від неправильного перекладу на латину арабського джиба, яке є транслітерацією слова на санскриті, що означало половину хорди, джа-ардха.^[2] Таблиця синусів містить числові значення функції синусу.

Визначення в контексті прямокутного трикутника

Для кута α, функція синусу задає відношення довжини протилежного до кута катету до довжини гіпотенузи, ${\displaystyle \sin \alpha ={\frac {\textrm {opposite}}{\textrm {hypotenuse}}}}$

При визначенні тригонометричних функцій для гострого кута α, беруть будь-який прямокутний трикутник який містить кут α; на відповідному малюнку, це геометричний кут A в трикутнику ABC, який має значення α. Три сторони трикутника мають назви:

• протилежний катет це сторона протилежна обраному куту, в даному випадку це сторона a.
• гіпотенуза це сторона протилежна прямому куту, в даному випадку це сторона h. Гіпотенуза завжди є найдовшою стороною прямокутного трикутника.
• прилеглий катет- сторона що залишилась, в даному випадку це сторона b. Це сторона, яка одночасно прилягає до вибраного кута (кут A) і до прямого кута трикутника.

У визначеному трикутнику, синус кута дорівнює довжині протилежного катету поділеному на довжину гіпотенузи (інші тригонометричні функції можуть визначатися аналогічним способом; наприклад, косинус кута є відношенням довжин прилеглого катету до гіпотенузи).

Як уже зазначалося, значення функції sin(α) залежить від вибраного прямокутного трикутника, який містить в собі кут величиною α. Однак, це не є важливим: оскільки всі такі трикутники є подібними, і співвідношення сторін буде однакове в усіх таких трикутниках.

В контексті одиничного кола

Ілюстрація одиничного кола. Радіус якого дорівнює 1. Змінна t задає значення Кута.

В тригонометрії, одиничне коло це коло з радіусом один і з центром в початку координат (0, 0) декартової системи координат.

Нехай існує довільна пряма через початок координат, яка утворює кут θ із додатною частиною осі x, і перетинає одиничне коло. x- і y-є координатами точки перетину прямої і кола, які дорівнюють cos θ і sin(θ), відповідно. Відстань від точки до початку координат завжди дорівнює 1.

На відміну від визначення в контексті прямокутного трикутника або кута нахилу, використовуючи одиничне коло значення кута можуть бути розширені до повного набору дійсних аргументів. В такому випадку функція синуса є періодичною.

Одиничне коло є в основі принципу побудови координатного транспортиру. При безперервному обертанні кута навколо своєї осі на 360 градусів можна бачити як координата транспортира зміщується по осі Y від -1 до 1. На осі Y в одиничному колі розміщені значення функції синуса.

Анімація показує як функція синусу (червона) ${\displaystyle y=\sin(\theta )}$ із значень y-координати (червона точка), що змінюється при окреслені точкою одиничного кола (зелена), і значення кута θ задаються радіанах.

Тотожності

Див. також: Список тригонометричних тотожностей

Точні тотожності (застосовуються до радіан): Застосовуються до всіх значень кута ${\displaystyle \theta }$.

${\displaystyle \sin(\theta )=\cos \left({\frac {\pi }{2}}-\theta \right)={\frac {1}{\csc(\theta )}}}$

Обернені

оберненим числом для синусу є косеканс, тобто обернене число для sin(A) записується як csc(A), або cosec(A). Косеканс задає відношення довжини гіпотенузу до довжини протилежного катету:

${\displaystyle \csc(A)={\frac {1}{\sin(A)}}={\frac {\textrm {hypotenuse}}{\textrm {opposite}}}={\frac {h}{a}}.}$

Зворотні функції

Головні значення функції arcsin(x) зображені на декартовій площині. Arcsin є зворотньою функцією від синусу.

Зворотньою функцією для синусу є арксинус (позначається як arcsin або asin) або обернений синус (sin^-1). Оскільки синус не має ін'єктивного відображення, арксинус не є точною зворотньою функцією, а є частковою зворотньою функцією. Наприклад, sin(0) = 0, але також і sin(π) = 0, sin(2π) = 0 і так далі. Звідси випливає, що функція арксинус багатозначна: arcsin(0) = 0, але також і arcsin(0) = π, arcsin(0) = 2π, і т. д.. Коли необхідно мати одне визначене значення, функція може бути обмежена до її головної області значень. Виходячи з цього обмеження, для кожного значення x в усій області значень, вираз arcsin(x) прийматиме лише одне значення, яке називається його головним значенням.

${\displaystyle \theta =\arcsin \left({\frac {\text{opposite}}{\text{hypotenuse}}}\right)=\sin ^{-1}\left({\frac {a}{h}}\right).}$

k є деяким цілим значенням:

${\displaystyle {\begin{aligned}\sin(y)=x\ \Leftrightarrow \ &y=\arcsin x+2\pi k,{\text{ or }}\\&y=\pi -\arcsin(x)+2\pi k\end{aligned}}}$

або у вигляді одного рівняння:

${\displaystyle \sin(y)=x\ \Leftrightarrow \ y=(-1)^{k}\arcsin(x)+\pi k}$

Arcsin задовольняє рівнянням:

${\displaystyle \sin(\arcsin(x))=x\!}$

і

${\displaystyle \arcsin(\sin(\theta ))=\theta \quad {\text{for }}-{\frac {\pi }{2}}\leq \theta \leq {\frac {\pi }{2}}.}$

Обчислення

Див. також: Таблиця інтегралів тригонометричних функцій

Для функції синус:

${\displaystyle f(x)=\sin(x)\,}$

Похідною є:

${\displaystyle f'(x)=\cos(x)\,}$

Первісною функції є:

${\displaystyle \int f(x)\,dx=-\cos x+C}$,

де C позначає сталу інтегрування.

Зв'язок із іншими тригонометричними функціями

Функції синусу і косинусу можуть бути зв'язані між собою різними виразами. Ці дві функції відрізняються фазою в 90°: ${\displaystyle \sin(\pi /2-x)}$ = ${\displaystyle \cos(x)}$ для всіх кутів x. А також, похідною функції sin(x) є cos(x).

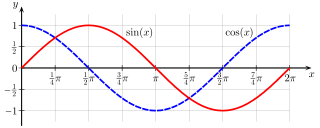
Будь-яку тригонометричну функцію можна виразити через інші тригонометричні функції (з урахуванням знаків плюс та мінус у різних чвертях або за допомогою знакової функції (sgn)).

Через інші тригонометричні функції синус можна виразити наступним чином:

	f θ	З використанням плюса/мінуса (±)					З використанням функції (sgn)
		f θ =	± по чвертям				f θ =
			I	II	III	IV
cos	${\displaystyle \sin(\theta )}$	${\displaystyle =\pm {\sqrt {1-\cos ^{2}(\theta )}}}$	+	+	−	−	${\displaystyle =\operatorname {sgn} \left(\cos \left(\theta -{\frac {\pi }{2}}\right)\right){\sqrt {1-\cos ^{2}(\theta )}}}$
	${\displaystyle \cos(\theta )}$	${\displaystyle =\pm {\sqrt {1-\sin ^{2}(\theta )}}}$	+	−	−	+	${\displaystyle =\operatorname {sgn} \left(\sin \left(\theta +{\frac {\pi }{2}}\right)\right){\sqrt {1-\sin ^{2}(\theta )}}}$
cot	${\displaystyle \sin(\theta )}$	${\displaystyle =\pm {\frac {1}{\sqrt {1+\cot ^{2}(\theta )}}}}$	+	+	−	−	${\displaystyle =\operatorname {sgn} \left(\cot \left({\frac {\theta }{2}}\right)\right){\frac {1}{\sqrt {1+\cot ^{2}(\theta )}}}}$
	${\displaystyle \cot(\theta )}$	${\displaystyle =\pm {\frac {\sqrt {1-\sin ^{2}(\theta )}}{\sin(\theta )}}}$	+	−	−	+	${\displaystyle =\operatorname {sgn} \left(\sin \left(\theta +{\frac {\pi }{2}}\right)\right){\frac {\sqrt {1-\sin ^{2}(\theta )}}{\sin(\theta )}}}$
tan	${\displaystyle \sin(\theta )}$	${\displaystyle =\pm {\frac {\tan(\theta )}{\sqrt {1+\tan ^{2}(\theta )}}}}$	+	−	−	+	${\displaystyle =\operatorname {sgn} \left(\tan \left({\frac {2\theta +\pi }{4}}\right)\right){\frac {\tan(\theta )}{\sqrt {1+\tan ^{2}(\theta )}}}}$
	${\displaystyle \tan(\theta )}$	${\displaystyle =\pm {\frac {\sin(\theta )}{\sqrt {1-\sin ^{2}(\theta )}}}}$	+	−	−	+	${\displaystyle =\operatorname {sgn} \left(\sin \left(\theta +{\frac {\pi }{2}}\right)\right){\frac {\sin(\theta )}{\sqrt {1-\sin ^{2}(\theta )}}}}$
sec	${\displaystyle \sin(\theta )}$	${\displaystyle =\pm {\frac {\sqrt {\sec ^{2}(\theta )-1}}{\sec(\theta )}}}$	+	−	+	−	${\displaystyle =\operatorname {sgn} \left(\sec \left({\frac {4\theta -\pi }{2}}\right)\right){\frac {\sqrt {\sec ^{2}(\theta )-1}}{\sec(\theta )}}}$
	${\displaystyle \sec(\theta )}$	${\displaystyle =\pm {\frac {1}{\sqrt {1-\sin ^{2}(\theta )}}}}$	+	−	−	+	${\displaystyle =\operatorname {sgn} \left(\sin \left(\theta +{\frac {\pi }{2}}\right)\right){\frac {1}{\sqrt {1-\sin ^{2}(\theta )}}}}$

Всі рівняння, в яких використовуються знаки плюс/мінус (±), мають додатні значення для кутів в першій чверті.

Основний зв'язок між синусом і косинусом може виражатися у вигляді Тригонометричної тотожності Піфагора:

${\displaystyle \cos ^{2}(\theta )+\sin ^{2}(\theta )=1\!}$

де sin²x означає (sin(x))².

Властивості пов'язані із чвертями

Чотири чверті Декартової системи координат.

В рамках чотирьох чвертей функція синусу має наступні властивості.

Чверть	Градуси	Радіани	Значення	Знак	Монотонність	Опуклість
1-а чверть	${\displaystyle 0^{\circ }<x<90^{\circ }}$	${\displaystyle 0<x<{\frac {\pi }{2}}}$	${\displaystyle 0<\sin(x)<1}$	${\displaystyle +}$	зростаюча	увігнута
2-а чверть	${\displaystyle 90^{\circ }<x<180^{\circ }}$	${\displaystyle {\frac {\pi }{2}}<x<\pi }$	${\displaystyle 0<\sin(x)<1}$	${\displaystyle +}$	спадна	увігнута
3-а чверть	${\displaystyle 180^{\circ }<x<270^{\circ }}$	${\displaystyle \pi <x<{\frac {3\pi }{2}}}$	${\displaystyle -1<\sin(x)<0}$	${\displaystyle -}$	спадна	опукла
4-а чверть	${\displaystyle 270^{\circ }<x<360^{\circ }}$	${\displaystyle {\frac {3\pi }{2}}<x<2\pi }$	${\displaystyle -1<\sin(x)<0}$	${\displaystyle -}$	зростаюча	опукла

Точки на межах чвертей. k є цілим числом.

Чверті одиничного кола і функції sin x, у Декартовій системі координат.

Градуси	Радіани ${\displaystyle 0\leq x<2\pi }$	Радіани	${\displaystyle \sin(x)}$	Тип точки
${\displaystyle 0^{\circ }}$	${\displaystyle 0}$	${\displaystyle 2\pi k}$	${\displaystyle 0}$	Корінь, Точка перегину
${\displaystyle 90^{\circ }}$	${\displaystyle {\frac {\pi }{2}}}$	${\displaystyle 2\pi k+{\frac {\pi }{2}}}$	${\displaystyle 1}$	Максимум
${\displaystyle 180^{\circ }}$	${\displaystyle \pi }$	${\displaystyle 2\pi k-\pi }$	${\displaystyle 0}$	Корінь, Точка перегину
${\displaystyle 270^{\circ }}$	${\displaystyle {\frac {3\pi }{2}}}$	${\displaystyle 2\pi k-{\frac {\pi }{2}}}$	${\displaystyle -1}$	Мінімум

Для аргументів, яких нема в цій таблиці, значення задані із урахуванням, що функція синусу є періодичною із періодом 360° (або 2π радіан): ${\displaystyle \sin(\alpha +360^{\circ })=\sin(\alpha )}$, або ${\displaystyle \sin(\alpha +180^{\circ })=-\sin(\alpha )}$. А також ${\displaystyle \cos(x)={\frac {e^{xi}+e^{-xi}}{2}}}$ і ${\displaystyle \sin(x)={\frac {e^{xi}-e^{-xi}}{2i}}}$. Для доповнення синусу, маємо ${\displaystyle \sin(180^{\circ }-\alpha )=\sin(\alpha )}$.

Див. також

• Тригонометричні функції
• Формула Ейлера
• Гіперболічні функції
• Теорема синусів
• Синусоїда
• Рівняння синус-Ґордона