Order-4 pentagonal tiling

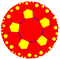
In geometry, the order-4 pentagonal tiling is a regular tiling of the hyperbolic plane. It has Schläfli symbol of {5,4}. It can also be called a pentapentagonal tiling in a bicolored quasiregular form.

Order-4 pentagonal tiling
Poincaré disk model of the hyperbolic plane
Type	Hyperbolic regular tiling
Vertex configuration	54
Schläfli symbol	{5,4} r{5,5} or ${\displaystyle {\begin{Bmatrix}5\\5\end{Bmatrix}}}$
Wythoff symbol	4 | 5 2 2 | 5 5
Coxeter diagram	or
Symmetry group	[5,4], (*542) [5,5], (*552)
Dual	Order-5 square tiling
Properties	Vertex-transitive, edge-transitive, face-transitive

Symmetry

This tiling represents a hyperbolic kaleidoscope of 5 mirrors meeting as edges of a regular pentagon. This symmetry by orbifold notation is called *22222 with 5 order-2 mirror intersections. In Coxeter notation can be represented as [5^*,4], removing two of three mirrors (passing through the pentagon center) in the [5,4] symmetry.

The kaleidoscopic domains can be seen as bicolored pentagons, representing mirror images of the fundamental domain. This coloring represents the uniform tiling t₁{5,5} and as a quasiregular tiling is called a pentapentagonal tiling.

Related polyhedra and tiling

Uniform pentagonal/square tilings v t e
Symmetry: [5,4], (*542)							[5,4]+, (542)	[5+,4], (5*2)	[5,4,1+], (*552)
{5,4}	t{5,4}	r{5,4}	2t{5,4}=t{4,5}	2r{5,4}={4,5}	rr{5,4}	tr{5,4}	sr{5,4}	s{5,4}	h{4,5}
Uniform duals
V54	V4.10.10	V4.5.4.5	V5.8.8	V45	V4.4.5.4	V4.8.10	V3.3.4.3.5	V3.3.5.3.5	V55

Uniform pentapentagonal tilings v t e
Symmetry: [5,5], (*552)							[5,5]+, (552)
=	=	=	=	=	=	=	=
Order-5 pentagonal tiling {5,5}	Truncated order-5 pentagonal tiling t{5,5}	Order-4 pentagonal tiling r{5,5}	Truncated order-5 pentagonal tiling 2t{5,5} = t{5,5}	Order-5 pentagonal tiling 2r{5,5} = {5,5}	Tetrapentagonal tiling rr{5,5}	Truncated order-4 pentagonal tiling tr{5,5}	Snub pentapentagonal tiling sr{5,5}
Uniform duals
Order-5 pentagonal tiling V5.5.5.5.5	V5.10.10	Order-5 square tiling V5.5.5.5	V5.10.10	Order-5 pentagonal tiling V5.5.5.5.5	V4.5.4.5	V4.10.10	V3.3.5.3.5

This tiling is topologically related as a part of sequence of regular polyhedra and tilings with pentagonal faces, starting with the dodecahedron, with Schläfli symbol {5,n}, and Coxeter diagram , progressing to infinity.

{5,n} tilings
{5,3}	{5,4}	{5,5}	{5,6}	{5,7}

This tiling is also topologically related as a part of sequence of regular polyhedra and tilings with four faces per vertex, starting with the octahedron, with Schläfli symbol {n,4}, and Coxeter diagram , with n progressing to infinity.

*n42 symmetry mutation of regular tilings: {n,4} v t e
Spherical		Euclidean	Hyperbolic tilings
24	34	44	54	64	74	84	...∞4

This tiling is topologically related as a part of sequence of regular polyhedra and tilings with vertex figure (4ⁿ).

*n42 symmetry mutation of regular tilings: {4,n} v t e
Spherical	Euclidean	Compact hyperbolic				Paracompact
{4,3}	{4,4}	{4,5}	{4,6}	{4,7}	{4,8}...	{4,∞}

*5n2 symmetry mutations of quasiregular tilings: (5.n)2 v t e
Symmetry *5n2 [n,5]	Spherical	Hyperbolic					Paracompact	Noncompact
	*352 [3,5]	*452 [4,5]	*552 [5,5]	*652 [6,5]	*752 [7,5]	*852 [8,5]...	*∞52 [∞,5]	[ni,5]
Figures
Config.	(5.3)2	(5.4)2	(5.5)2	(5.6)2	(5.7)2	(5.8)2	(5.∞)2	(5.ni)2
Rhombic figures
Config.	V(5.3)2	V(5.4)2	V(5.5)2	V(5.6)2	V(5.7)2	V(5.8)2	V(5.∞)2	V(5.∞)2

References

• John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
• Coxeter, H. S. M. (1999), Chapter 10: Regular honeycombs in hyperbolic space (PDF), The Beauty of Geometry: Twelve Essays, Dover Publications, ISBN 0-486-40919-8, LCCN 99035678, invited lecture, ICM, Amsterdam, 1954.

See also

• Square tiling
• Tilings of regular polygons
• List of uniform planar tilings
• List of regular polytopes

External links

• Weisstein, Eric W. "Hyperbolic tiling". MathWorld.
• Weisstein, Eric W. "Poincaré hyperbolic disk". MathWorld.
• Hyperbolic and Spherical Tiling Gallery
• KaleidoTile 3: Educational software to create spherical, planar and hyperbolic tilings
• Hyperbolic Planar Tessellations, Don Hatch