Order-6 square tiling

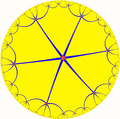
In geometry, the order-6 square tiling is a regular tiling of the hyperbolic plane. It has Schläfli symbol of {4,6}.

Order-6 square tiling
Poincaré disk model of the hyperbolic plane
Type	Hyperbolic regular tiling
Vertex configuration	46
Schläfli symbol	{4,6}
Wythoff symbol	6 | 4 2
Coxeter diagram
Symmetry group	[6,4], (*642)
Dual	Order-4 hexagonal tiling
Properties	Vertex-transitive, edge-transitive, face-transitive

Symmetry

This tiling represents a hyperbolic kaleidoscope of 4 mirrors meeting as edges of a square, with six squares around every vertex. This symmetry by orbifold notation is called (*3333) with 4 order-3 mirror intersections. In Coxeter notation can be represented as [6,4^*], removing two of three mirrors (passing through the square center) in the [6,4] symmetry. The *3333 symmetry can be doubled to 663 symmetry by adding a mirror bisecting the fundamental domain.

This bicolored square tiling shows the even/odd reflective fundamental square domains of this symmetry. This bicolored tiling has a wythoff construction t₁{(4,4,3)}. A second 6-color symmetry can be constructed from a hexagonal symmetry domain.

[4,6,1+] = [(4,4,3)] or (*443) symmetry =	[4,6*] = (*222222) symmetry =

Example artwork

Around 1956, M.C. Escher explored the concept of representing infinity on a two-dimensional plane. Discussions with Canadian mathematician H.S.M. Coxeter inspired Escher's interest in hyperbolic tessellations, which are regular tilings of the hyperbolic plane. Escher's wood engravings Circle Limit I–IV demonstrate this concept. The last one Circle Limit IV (Heaven and Hell), (1960) tiles repeating angels and devils by (*3333) symmetry on a hyperbolic plane in a Poincaré disk projection.

The artwork seen below has an approximate hyperbolic mirror overlay added to show the square symmetry domains of the order-6 square tiling. If you look closely, you can see one of four angels and devils around each square are drawn as back sides. Without this variation, the art would have a 4-fold gyration point at the center of each square, giving (4*3), [6,4⁺] symmetry.^[1]

Related polyhedra and tiling

This tiling is topologically related as a part of sequence of regular polyhedra and tilings with vertex figure (4ⁿ).

*n42 symmetry mutation of regular tilings: {4,n} v t e
Spherical	Euclidean	Compact hyperbolic				Paracompact
{4,3}	{4,4}	{4,5}	{4,6}	{4,7}	{4,8}...	{4,∞}

This tiling is topologically related as a part of sequence of regular tilings with order-6 vertices with Schläfli symbol {n,6}, and Coxeter diagram , progressing to infinity.

Regular tilings {n,6} v t e
Spherical	Euclidean	Hyperbolic tilings
{2,6}	{3,6}	{4,6}	{5,6}	{6,6}	{7,6}	{8,6}	...	{∞,6}

Uniform tetrahexagonal tilings v t e
Symmetry: [6,4], (*642) (with [6,6] (*662), [(4,3,3)] (*443) , [∞,3,∞] (*3222) index 2 subsymmetries) (And [(∞,3,∞,3)] (*3232) index 4 subsymmetry)
= = =	=	= = =	=	= = =	=
{6,4}	t{6,4}	r{6,4}	t{4,6}	{4,6}	rr{6,4}	tr{6,4}
Uniform duals
V64	V4.12.12	V(4.6)2	V6.8.8	V46	V4.4.4.6	V4.8.12
Alternations
[1+,6,4] (*443)	[6+,4] (6*2)	[6,1+,4] (*3222)	[6,4+] (4*3)	[6,4,1+] (*662)	[(6,4,2+)] (2*32)	[6,4]+ (642)
=	=	=	=	=	=
h{6,4}	s{6,4}	hr{6,4}	s{4,6}	h{4,6}	hrr{6,4}	sr{6,4}

Uniform (4,4,3) tilings v t e
Symmetry: [(4,4,3)] (*443)							[(4,4,3)]+ (443)	[(4,4,3+)] (3*22)	[(4,1+,4,3)] (*3232)
h{6,4} t0(4,4,3)	h2{6,4} t0,1(4,4,3)	{4,6}1/2 t1(4,4,3)	h2{6,4} t1,2(4,4,3)	h{6,4} t2(4,4,3)	r{6,4}1/2 t0,2(4,4,3)	t{4,6}1/2 t0,1,2(4,4,3)	s{4,6}1/2 s(4,4,3)	hr{4,6}1/2 hr(4,3,4)	h{4,6}1/2 h(4,3,4)	q{4,6} h1(4,3,4)
Uniform duals
V(3.4)4	V3.8.4.8	V(4.4)3	V3.8.4.8	V(3.4)4	V4.6.4.6	V6.8.8	V3.3.3.4.3.4	V(4.4.3)2	V66	V4.3.4.6.6

Uniform tilings in symmetry *3222 v t e
64	6.6.4.4	(3.4.4)2	4.3.4.3.3.3
6.6.4.4	6.4.4.4	3.4.4.4.4
(3.4.4)2	3.4.4.4.4	46

See also

• Square tiling
• Uniform tilings in hyperbolic plane
• List of regular polytopes