Snub order-6 square tiling

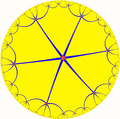
In geometry, the snub order-6 square tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of s{(4,4,3)} or s{4,6}.

Snub order-6 square tiling
Poincaré disk model of the hyperbolic plane
Type	Hyperbolic uniform tiling
Vertex configuration	3.3.3.4.3.4
Schläfli symbol	s(4,4,3) s{4,6}
Wythoff symbol	| 4 4 3
Coxeter diagram
Symmetry group	[(4,4,3)]+, (443) [6,4+], (4*3)
Dual	Order-4-4-3 snub dual tiling
Properties	Vertex-transitive

Images

Symmetry

The symmetry is doubled as a snub order-6 square tiling, with only one color of square. It has Schläfli symbol of s{4,6}.

Related polyhedra and tiling

The vertex figure 3.3.3.4.3.4 does not uniquely generate a uniform hyperbolic tiling. Another with quadrilateral fundamental domain (3 2 2 2) and 2*32 symmetry is generated by :

Uniform (4,4,3) tilings v t e
Symmetry: [(4,4,3)] (*443)							[(4,4,3)]+ (443)	[(4,4,3+)] (3*22)	[(4,1+,4,3)] (*3232)
h{6,4} t0(4,4,3)	h2{6,4} t0,1(4,4,3)	{4,6}1/2 t1(4,4,3)	h2{6,4} t1,2(4,4,3)	h{6,4} t2(4,4,3)	r{6,4}1/2 t0,2(4,4,3)	t{4,6}1/2 t0,1,2(4,4,3)	s{4,6}1/2 s(4,4,3)	hr{4,6}1/2 hr(4,3,4)	h{4,6}1/2 h(4,3,4)	q{4,6} h1(4,3,4)
Uniform duals
V(3.4)4	V3.8.4.8	V(4.4)3	V3.8.4.8	V(3.4)4	V4.6.4.6	V6.8.8	V3.3.3.4.3.4	V(4.4.3)2	V66	V4.3.4.6.6

Uniform tetrahexagonal tilings v t e
Symmetry: [6,4], (*642) (with [6,6] (*662), [(4,3,3)] (*443) , [∞,3,∞] (*3222) index 2 subsymmetries) (And [(∞,3,∞,3)] (*3232) index 4 subsymmetry)
= = =	=	= = =	=	= = =	=
{6,4}	t{6,4}	r{6,4}	t{4,6}	{4,6}	rr{6,4}	tr{6,4}
Uniform duals
V64	V4.12.12	V(4.6)2	V6.8.8	V46	V4.4.4.6	V4.8.12
Alternations
[1+,6,4] (*443)	[6+,4] (6*2)	[6,1+,4] (*3222)	[6,4+] (4*3)	[6,4,1+] (*662)	[(6,4,2+)] (2*32)	[6,4]+ (642)
=	=	=	=	=	=
h{6,4}	s{6,4}	hr{6,4}	s{4,6}	h{4,6}	hrr{6,4}	sr{6,4}

See also

• Square tiling
• Uniform tilings in hyperbolic plane
• List of regular polytopes