Poliedro uniforme

Un poliedro uniforme es una figura tridimensional que tiene polígonos regulares como caras y es isogonal (es decir, presenta una isometría que permite hacer corresponder el conjunto de sus vértices entre sí mediante relaciones de simetría). De ello se deduce que todos sus vértices son congruentes.^[1]

Los cinco sólidos platónicos

Los poliedros uniformes pueden ser regulares (si también son transitivos con respecto a caras y aristas), cuasirregulares (si son transitivos con respecto a sus aristas pero no con respecto a sus caras) o semirregulares (si no son transitivos de aristas ni de caras). No es necesario que la configuración de caras y de vértices sea convexa, por lo que muchos de los poliedros uniformes también son poliedros estrellados.

Hay dos clases infinitas de poliedros uniformes, junto con otros 75 poliedros:^[2]

• Clases infinitas:
  • Prismas
  • Antiprismas
• Convexos excepcionales:
  • 5 sólidos platónicos: poliedros convexos regulares
  • 13 sólidos arquimedianos: 2 poliedros convexos cuasirregulares y 11 semirregulares
• Estrellas (no convexos) excepcionales:
  • 4 sólidos de Kepler-Poinsot: poliedros regulares no convexos
  • 53 poliedros uniformes estrellados: 5 cuasirregulares y 48 semirregulares.

Por tanto, 5 + 13 + 4 + 53 = 75.

También hay muchos poliedros uniformes degenerados con pares de bordes que coinciden, incluido uno encontrado por John Skilling denominado gran dirrombidodecaedro birromo (figura de Skilling).

Los poliedros conjugados de los poliedros uniformes son figuras isoedrales (es decir, isoédricas), presentan figuras de vértice regulares, y generalmente se clasifican en paralelo con su poliedro dual (uniforme). El dual de un poliedro regular es regular, mientras que el dual de un sólido de Arquímedes es un sólido de Catalan.

El concepto de poliedro uniforme es un caso especial del concepto de politopo uniforme, que también se aplica a las formas en el espacio de dimensiones superiores e inferiores.

Definición

El pecado original en la teoría de los poliedros se remonta a Euclides, y a través de Kepler, Poinsot, Cauchy y muchos otros continúa afligiendo a todo el trabajo sobre este tema (incluido el del presente autor). Surge del hecho de que el uso tradicional del término "poliedros regulares" era, y es, contrario a la sintaxis y a la lógica: las palabras parecen implicar que estamos tratando, entre los objetos que llamamos "poliedros", con aquellos especiales, los que merecen ser llamados "regulares". Pero en cada etapa —Euclides, Kepler, Poinsot, Hess, Brückner, …— los distintos autores no lograron definir cuáles son los "poliedros" entre los que encuentran los "regulares". Branko Grünbaum (1994)[3]

Coxeter, Longuet-Higgins y Miller (1954) definen los poliedros uniformes como poliedros con caras regulares y transitividad entre sus vértices (es decir, con propiedades de isoedría). A su vez, definen un poliedro como un conjunto finito de polígonos, de modo que cada lado de un polígono es un lado de otro polígono, de modo que ningún subconjunto propio no vacío de los polígonos tiene la misma propiedad. Por polígono se refieren implícitamente a un polígono en un espacio euclídeo tridimensional; se permite que no sean convexos y que sus aristas se crucen entre sí.^[4]

Hay algunas generalizaciones del concepto de poliedro uniforme. Si se descarta el supuesto de conectividad, se obtienen sólidos compuestos uniformes, que se pueden considerar como la unión de poliedros (como por ejemplo, el compuesto de 5 cubos). Si se deja de lado la condición de que la configuración del poliedro no sea degenerada, se obtienen los llamados poliedros uniformes degenerados, que requieren una definición más general del concepto de poliedro.Grünbaum (1994) dio una definición bastante complicada de poliedro, mientras que McMullen y Schulte (2002) dio una definición más simple y general: en su terminología, un poliedro es un politopo abstracto bidimensional con una realización tridimensional no degenerada. Aquí, politopo abstracto es el conjunto de sus caras que satisfacen varias condiciones, una realización es una función desde sus vértices a algún espacio, y la realización se llama no degenerada si dos caras distintas del politopo abstracto tienen realizaciones distintas.

Algunas de las formas en que pueden dar lugar a poliedros degenerados son las siguientes:

• Caras ocultas. Algunos poliedros tienen caras que están ocultas, en el sentido de que ningún punto de su interior puede verse desde el exterior. Por lo general, estos no se cuentan como poliedros uniformes.
• Compuestos degenerados. Algunos poliedros tienen múltiples aristas y sus caras son las caras de dos o más poliedros, aunque estos no son compuestos en el sentido anterior, ya que los poliedros comparten aristas.
• Recubrimientos duplicados. Existen algunos poliedros no orientables que tienen recubrimientos duplicados que satisfacen la definición de un poliedro uniforme. Hay recubrimientos dobles con caras, aristas y vértices duplicados.Por lo general, no se cuentan como poliedros uniformes.
• Caras dobles. Hay varios poliedros con caras dobles producidos por la construcción de Wythoff. La mayoría de los autores no permiten la presencia de caras dobles y las eliminan como parte de la construcción.
• Aristas dobles. La figura de Skilling tiene la propiedad de que posee aristas dobles (como en los poliedros uniformes degenerados) pero sus caras no se pueden considerar como la unión de dos poliedros uniformes.

Historia

Poliedros convexos regulares

• Los sólidos platónicos se remontan a la Grecia clásica, y fueron estudiados por los pitagóricos, Platón (c. 424-348 a. C.), Teeteto (c. 417-369 a. C.), Timeo (c. 420-380 a. C.) y Euclides (c. 300 a. C.). También se sabe que los etruscos habían descubierto el dodecaedro regular antes del año 500 a. C.^[5]

Poliedros convexos uniformes no regulares

Los sólidos arquimedianos, por Johannes Kepler

• El cuboctaedro era conocido por Platón.
• Arquímedes (287-212 a. C.) descubrió los 13 sólidos arquimedianos. Su libro original sobre el tema se perdió, pero Papo de Alejandría (c. 290-350 d. C.) mencionó que Arquímedes había enumerado 13 poliedros.
• Piero della Francesca (1415-1492) redescubrió los cinco truncamientos de los sólidos platónicos: tetraedro truncado, octaedro truncado, cubo truncado, dodecaedro truncado e icosaedro truncado, e incluyó ilustraciones y cálculos de sus propiedades métricas en su libro De quinque corporibus regularibus. También habló del cuboctaedro en un libro diferente.^[6]
• Luca Pacioli plagió el trabajo de Piero della Francesca en De divina proportione en 1509, agregando el rombicuboctaedro, llamándolo icosihexaedro por sus 26 caras. Este sólido sería dibujado por Leonardo da Vinci.
• Johannes Kepler (1571-1630) fue el primero en publicar la lista completa de los sólidos arquimedianos en 1619, y también identificó las familias infinitas de prismas y antiprismas uniformes.

Poliedros estrellados regulares

• Kepler (1619) descubrió dos de los denominados sólidos de Kepler-Poinsot regulares; y Louis Poinsot (1809) descubrió los otros dos. Augustin Louis Cauchy (1789-1857) demostró que los cuatro sólidos forman un conjunto completo, y Arthur Cayley (1821-1895) acuñó la denominación con la que son conocidos.

Otros 53 poliedros estrellados no regulares

• De los 53 restantes, Edmund Hess (1878) descubrió dos, Albert Badoureau (1881) descubrió 36 más y Pitsch (1881) descubrió de forma independiente 18 más, de los cuales 3 no habían sido descubiertos previamente. Conjuntamente, estos tres autores identificaron 41 poliedros.
• El geómetra H.S.M. Coxeter descubrió los doce restantes en colaboración con J. C. P. Miller (1930-1932) pero no los publicó. M.S. Longuet-Higgins y H.C. Longuet-Higgins descubrieron de forma independiente once de estos sólidos. Lesavre y Mercier redescubrieron cinco de ellos en 1947.
• Coxeter, Longuet-Higgins y Miller (1954) publicó la lista de poliedros uniformes.
• Sopov (1970) demostró su conjetura de que la lista estaba completa.
• En 1974, Magnus Wenninger publicó su libro Polyhedron models, que enumera los 75 poliedros uniformes no prismáticos, con muchos nombres inéditos que les dio Norman Johnson.
• Skilling (1975) demostró de forma independiente la integridad del conjunto, y demostró que si la definición de poliedro uniforme se relaja para permitir que las aristas coincidan, solo hay una posibilidad adicional.
• En 1987, Edmond Bonan dibujó todos los poliedros uniformes y sus duales en 3D utilizando un programa compilado en Turbo Pascal denominado Polyca: muchos de ellos se mostraron durante el Congreso de la Unión Estereoscópica Internacional celebrado en el Congress Theatre, de Eastbourne, United Reino.^[7]
• En 1993, Zvi Har'El produjo una construcción caleidoscópica completa de los poliedros uniformes y duales con un programa de computadora llamado Kaleido, resumido en un documento titulado Solución uniforme para poliedros uniformes, numerando las figuras del 1 al 80.^[8]
• También en 1993, R. Mäder portó esta solución de Kaleido a Mathematica con un sistema de indexación ligeramente diferente.^[9]
• En 2002 Peter W. Messer descubrió un conjunto mínimo de expresiones de forma cerrada para determinar las principales cantidades combinatorias y métricas de cualquier poliedro uniforme (y de su dual) a partir únicamente de su símbolo de Wythoff.^[10][11]

Poliedros estrellados uniformes

El gran dirhombicosidodecaedro, el único poliedro uniforme no wythoffiano

Artículo principal: Poliedro uniforme estrellado

Las 57 formas no prismáticas no convexas, con la excepción del gran dirhombicosidodecaedro, son compiladas por construcciones de Wythoff dentro de los triángulos de Schwarz.

Construcción de formas convexas de Wythoff

Los poliedros uniformes convexos se pueden nombrar mediante operaciones de construcción de Wythoff sobre una forma regular. Para más detalle, más adelante se dan los poliedros uniformes convexos por su construcción de Wythoff dentro de cada grupo de simetría.

Dentro de la construcción de Wythoff, hay repeticiones creadas por formas de simetría más baja. El cubo es un poliedro regular y un prisma cuadrado. El octaedro es un poliedro regular y un antiprisma triangular. El octaedro también es un tetraedro rectificado. Muchos poliedros se repiten a partir de diferentes fuentes de construcción y están coloreados de manera diferente.

La construcción de Wythoff se aplica igualmente a poliedros uniformes y teselados uniformes en la superficie de una esfera, por lo que se dan imágenes de ambos. Los mosaicos esféricos incluyen el conjunto del hosoedro y del diedro, que son poliedros degenerados.

Estos grupos de simetría se forman a partir de los grupos de puntos en tres dimensiones reflexivos, cada uno representado por un triángulo fundamental (p q r), donde p > 1, q > 1, r > 1 y 1/p + 1/q + 1/r < 1.

• Simetría tetraédrica (3 3 2) - orden 24
• Simetría octaédrica (4 3 2) - orden 48
• Simetría icosaédrica (5 3 2) - orden 120
• Grupo diedral (n 2 2), para n = 3, 4, 5, ... - orden 4n

Las formas no reflexivas restantes se construyen mediante operaciones de alternación aplicadas a los poliedros con un número par de lados.

Junto con los prismas y su grupo diedral, el proceso de construcción esférico de Wythoff agrega dos clases regulares que se degeneran como poliedros: el diedro y el hosoedro, el primero con solo dos caras, y el segundo con solo dos vértices. El truncamiento del hosoedro regular crea los prismas.

Debajo de los poliedros uniformes convexos se indexan de 1 a 18 las formas no prismáticas, que se presentan en las tablas por forma de simetría.

Para el conjunto infinito de formas prismáticas, están indexadas en cuatro familias:

1. Hosoedros H_2... (solo como teselados esféricos)
2. Diedros D_2... (solo como teselados esféricos)
3. Prismas P_3... (hosoedros truncados)
4. Antiprismas A_3... (prismas achatados o romos)

Tablas resumen

Nombre de Johnson	Relacionado	Truncado	Rectificado	Bitruncado (tr. dual)	Birrectificado (dual)	Canteado	Omnitruncado (cantitruncado)	Romo
Diagrama de Coxeter-Dynkin
Símbolo de Schläfli extendido	${\displaystyle {\begin{Bmatrix}p,q\end{Bmatrix}}}$	${\displaystyle t{\begin{Bmatrix}p,q\end{Bmatrix}}}$	${\displaystyle {\begin{Bmatrix}p\\q\end{Bmatrix}}}$	${\displaystyle t{\begin{Bmatrix}q,p\end{Bmatrix}}}$	${\displaystyle {\begin{Bmatrix}q,p\end{Bmatrix}}}$	${\displaystyle r{\begin{Bmatrix}p\\q\end{Bmatrix}}}$	${\displaystyle t{\begin{Bmatrix}p\\q\end{Bmatrix}}}$	${\displaystyle s{\begin{Bmatrix}p\\q\end{Bmatrix}}}$
	{p,q}	t{p,q}	r{p,q}	2t{p,q}	2r{p,q}	rr{p,q}	tr{p,q}	sr{p,q}
	t0{p,q}	t0,1{p,q}	t1{p,q}	t1,2{p,q}	t2{p,q}	t0,2{p,q}	t0,1,2{p,q}	ht0,1,2{p,q}
Símbolo de Wythoff (p q 2)	q | p 2	2 q | p	2 | p q	2 p | q	p | q 2	p q | 2	p q 2 |	| p q 2
Configuración de vértices	pq	q.2p.2p	(p.q)2	p.2q.2q	qp	p.4.q.4	4.2p.2q	3.3.p.3.q
Simetría Tetraédrica (3 3 2)	3.3.3	3.6.6	3.3.3.3	3.6.6	3.3.3	3.4.3.4	4.6.6	3.3.3.3.3
Simetría Otaédrica (4 3 2)	4.4.4	3.8.8	3.4.3.4	4.6.6	3.3.3.3	3.4.4.4	4.6.8	3.3.3.3.4
Simetría Icosaédrica (5 3 2)	5.5.5	3.10.10	3.5.3.5	5.6.6	3.3.3.3.3	3.4.5.4	4.6.10	3.3.3.3.5

Muestra de simetrías diédricas:

(La esfera no se corta, solo se corta el teselado). (En una esfera, una arista es el arco de un círculo máximo, el camino más corto, entre sus dos vértices. Por lo tanto, un digóno cuyos vértices no están opuestos polarmente es plano: parece una arista)

(p 2 2)	Relacionado	Truncado	Rectificado	Bitruncado (tr. dual)	Birrectificado (dual)	Canteado	Omnitruncado (cantitruncado)	Romo
Diagrama de Coxeter-Dynkin
Símbolo de Schläfli extendido	${\displaystyle {\begin{Bmatrix}p,2\end{Bmatrix}}}$	${\displaystyle t{\begin{Bmatrix}p,2\end{Bmatrix}}}$	${\displaystyle {\begin{Bmatrix}p\\2\end{Bmatrix}}}$	${\displaystyle t{\begin{Bmatrix}2,p\end{Bmatrix}}}$	${\displaystyle {\begin{Bmatrix}2,p\end{Bmatrix}}}$	${\displaystyle r{\begin{Bmatrix}p\\2\end{Bmatrix}}}$	${\displaystyle t{\begin{Bmatrix}p\\2\end{Bmatrix}}}$	${\displaystyle s{\begin{Bmatrix}p\\2\end{Bmatrix}}}$
	{p,2}	t{p,2}	r{p,2}	2t{p,2}	2r{p,2}	rr{p,2}	tr{p,2}	sr{p,2}
	t0{p,2}	t0,1{p,2}	t1{p,2}	t1,2{p,2}	t2{p,2}	t0,2{p,2}	t0,1,2{p,2}	ht0,1,2{p,2}
Símbolo de Wythoff	2 | p 2	2 2 | p	2 | p 2	2 p | 2	p | 2 2	p 2 | 2	p 2 2 |	| p 2 2
Vertex figure	p2	2.2p.2p	p.2.p.2	p.4.4	2p	p.4.2.4	4.2p.4	3.3.3.p
Diedral (2 2 2)	{2,2}	2.4.4	2.2.2.2	4.4.2	2.2	2.4.2.4	4.4.4	3.3.3.2
Diedral (3 2 2)	3.3	2.6.6	2.3.2.3	4.4.3	2.2.2	2.4.3.4	4.4.6	3.3.3.3
Diedral (4 2 2)	4.4	2.8.8	2.4.2.4	4.4.4	2.2.2.2	2.4.4.4	4.4.8	3.3.3.4
Diedral (5 2 2)	5.5	2.10.10	2.5.2.5	4.4.5	2.2.2.2.2	2.4.5.4	4.4.10	3.3.3.5
Diedral (6 2 2)	6.6	2.12.12	2.6.2.6	4.4.6	2.2.2.2.2.2	2.4.6.4	4.4.12	3.3.3.6

Simetría tetraédrica (3 3 2) T_d

La simetría tetraédrica de la esfera genera 5 poliedros uniformes y una sexta forma mediante una operación de suavizado (poliedro romo).

La simetría tetraédrica está representada por un triángulo fundamental con un vértice con dos simetrías de reflexión y dos vértices con tres simetrías de reflexión, representado por el símbolo (3 3 2). También puede estar representado por el grupo de Coxeter A₂ o [3,3], así como por el diagrama de Coxeter-Dynkin: .

Hay 24 triángulos, visibles en las caras del tetraquishexaedro y en los triángulos de la esfera coloreados alternativamente:

#	Nombre	Grafo A3	Grafo A2	Imagen	Teselado	Figura de vértice	Símbolos de Coxeter y de Schläfli	Número de caras por posición			Número de elementos
								Pos. 2 [3] (4)	Pos. 1 [2] (6)	Pos. 0 [3] (4)	Caras	Aristas	Vértices
1	Tetraedro						{3,3}	{3}			4	6	4
[1]	Birectified tetrahedron (same as tetraedro)						t2{3,3}={3,3}			{3}	4	6	4
2	Rectified tetrahedron Tetratetraedro (como un octaedro)						t1{3,3}=r{3,3}	{3}		{3}	8	12	6
3	Tetraedro truncado						t0,1{3,3}=t{3,3}	{6}		{3}	8	18	12
[3]	Tetraedro bitruncado (como un tetraedro truncado)						t1,2{3,3}=t{3,3}	{3}		{6}	8	18	12
4	Tetraedro canteado Rombitetratetraedro (como un cuboctaedro)						t0,2{3,3}=rr{3,3}	{3}	{4}	{3}	14	24	12
5	Tetraedro omnitruncado Tetratetraedro truncado (como un octaedro truncado)						t0,1,2{3,3}=tr{3,3}	{6}	{4}	{6}	14	36	24
6	Tetratetraedro achatado (como un icosaedro)						sr{3,3}	{3}	2 {3}	{3}	20	30	12

Simetría octaédrica (4 3 2) O_h

La simetría octaédrica de la esfera genera 7 poliedros uniformes y 7 más por alternancia. Seis de estas formas se repiten de la tabla de simetría tetraédrica anterior.

La simetría octaédrica está representada por un triángulo fundamental (4 3 2) contando las reflexiones en cada vértice. También se puede representar con el grupo de Coxeter B₂ o [4,3], así como con el diagrama de Coxeter-Dynkin: .

Hay 48 triángulos, visibles en las caras del hexaquisoctaedro y en los triángulos de colores alternados en una esfera:

#	Nombre	Grafo B3	Grafo B2	Imagen	Teselado	Figura de vértice	Símbolos de Coxeter y de Schläfli	Número de caras por posición			Número de elementos
								Pos. 2 [4] (6)	Pos. 1 [2] (12)	Pos. 0 [3] (8)	Caras	Aristas	Vértices
7	Cubo						{4,3}	{4}			6	12	8
[2]	Octaedro						{3,4}			{3}	8	12	6
[4]	Cubo rectificado Octaedro rectificado (Cuboctaedro)						{4,3}	{4}		{3}	14	24	12
8	Cubo truncado						t0,1{4,3}=t{4,3}	{8}		{3}	14	36	24
[5]	Octaedro truncado						t0,1{3,4}=t{3,4}	{4}		{6}	14	36	24
9	Cubo canteado Octaedro canteado Rombicuboctaedro						t0,2{4,3}=rr{4,3}	{4}	{4}	{3}	26	48	24
10	Cubo omnitruncado Octaedro omnitruncado Cuboctaedro truncado						t0,1,2{4,3}=tr{4,3}	{8}	{4}	{6}	26	72	48
[6]	Octaedro achatado (como un icosaedro)						= s{3,4}=sr{3,3}		{3}	{3}	20	30	12
[1]	Semicubo (como un tetraedro)						= h{4,3}={3,3}	1/2 {3}			4	6	4
[2]	Cubo canteado (como un tetraedro truncado)						= h2{4,3}=t{3,3}	1/2 {6}		1/2 {3}	8	18	12
[4]	(como un cuboctaedro)						= rr{3,3}				14	24	12
[5]	(como un octaedro truncado)						= tr{3,3}				14	36	24
[9]	Octaedro achatado canteado (como un rombicuboctaedro)						s2{3,4}=rr{3,4}				26	48	24
11	Cuboctaedro achatado						sr{4,3}	{4}	2 {3}	{3}	38	60	24

Simetría icosaédrica (5 3 2) I_h

Véase también: Simetría icosaédrica

La simetría icosaédrica de la esfera genera 7 poliedros uniformes y 1 más por alternancia. Solo uno se repite de la tabla de simetría tetraédrica y octaédrica anterior.

La simetría icosaédrica está representada por un triángulo fundamental (5 3 2) contando las reflexiones en cada vértice. También se puede representar mediante el grupo de Coxeter G₂ o [5,3], así como por un diagrama de Coxeter-Dynkin: .

Hay 120 triángulos, visibles en las caras del hexaquisicosaedro y en los triángulos de colores alternados en una esfera:

#	Nombre	Grafo (A2) [6]	Grafo (H3) [10]	Imagen	Teselado	Figura de vértice	Símbolos de Coxeter y de Schläfli	Número de caras por posición			Número de elementos
								Pos. 2 [5] (12)	Pos. 1 [2] (30)	Pos. 0 [3] (20)	Caras	Aristas	Vértices
12	Dodecaedro						{5,3}	{5}			12	30	20
[6]	Icosaedro						{3,5}			{3}	20	30	12
13	Dodecaedro rectificado Icosaedro rectificado Icosidodecaedro						t1{5,3}=r{5,3}	{5}		{3}	32	60	30
14	Dodecaedro truncado						t0,1{5,3}=t{5,3}	{10}		{3}	32	90	60
15	Icosaedro truncado						t0,1{3,5}=t{3,5}	{5}		{6}	32	90	60
16	Dodecaedro canteado Icosaedro canteado Rombicosidodecaedro						t0,2{5,3}=rr{5,3}	{5}	{4}	{3}	62	120	60
17	Dodecaedro omnitruncado Icosaedro omnitruncado Icosidodecaedro truncado						t0,1,2{5,3}=tr{5,3}	{10}	{4}	{6}	62	180	120
18	Icosidodecaedro achatado						sr{5,3}	{5}	2 {3}	{3}	92	150	60

Simetría diédrica D_ph: (p 2 2) prismática [p, 2] y familia I₂(p)

Artículo principal: Poliedro prismático uniforme

El grupo diedral de la esfera genera dos conjuntos infinitos de poliedros uniformes (prismas y antiprismas,) y dos conjuntos infinitos más de poliedros degenerados, el hosoedro y el diedro que existen como teselas en la esfera.

La simetría diédrica o diedral está representada por un triángulo fundamental (p 2 2) contando las reflexiones en cada vértice. También puede estar representado por el grupo de Coxeter I₂ (p) o [n, 2], así como por un diagrama de Coxeter-Dynkin prismático: .

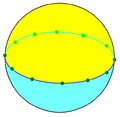
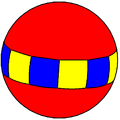
A continuación se muestran las primeras cinco simetrías diédricas: D₂ ... D₆. La simetría diedral D_p tiene orden 4n, representa las caras de una bipirámide, y en la esfera como una línea del ecuador y n líneas de longitud igualmente espaciadas.

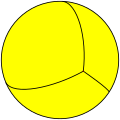
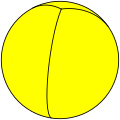
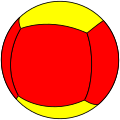
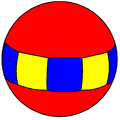
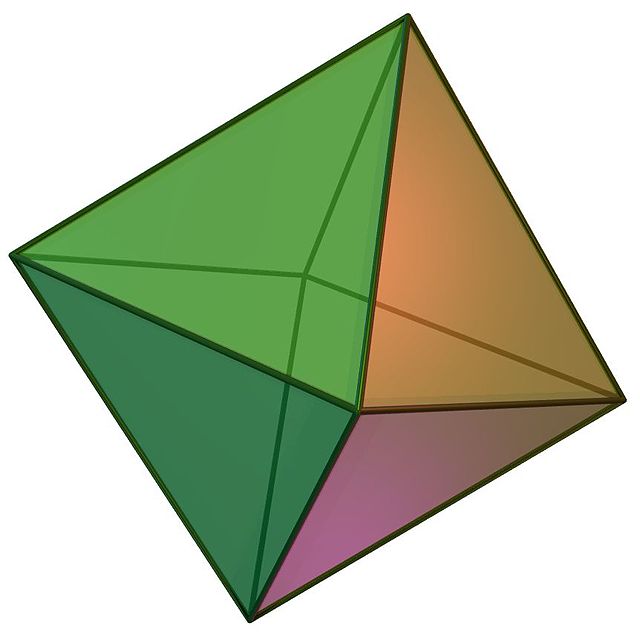
(2 2 2) Simetría diédrica

Hay 8 triángulos fundamentales, visibles en las caras del octaedro y en los triángulos de colores alternados en una esfera:

#	Nombre	Imagen	Teselado	Figura de vértice	Símbolos de Coxeter y de Schläfli	Número de caras por posición			Número de elementos
						Pos. 2 [2] (2)	Pos. 1 [2] (2)	Pos. 0 [2] (2)	Caras	Aristas	Vértices
D2 H2	Diedro digonal, Hosoedro digonal				{2,2}	{2}			2	2	2
D4	Diedro digonal truncado (como un diedro cuadrado)				t {2.2} = {4.2}	{4}			2	4	4
P4 [7]	Diedro digonal omnitruncado (como un cubo)				t0,1,2 {2,2} = tr {2,2}	{4}	{4}	{4}	6	12	8
A2 [1]	Diedro digonal achatado (como un tetraedro)				sr {2,2}		2 {3}		4	6	4

Simetría diédrica (3 2 2) D_3h

Hay 12 triángulos fundamentales, visibles en las caras de la bipirámide hexagonal y como triángulos de colores alternados en una esfera:

#	Nombre	Imagen	Teselado	Figura de vértice	Símbolos de Coxeter y de Schläfli	Número de caras por posición			Número de elementos
						Pos. 2 [3] (2)	Pos. 1 [2] (3)	Pos. 0 [2] (3)	Caras	Aristas	Vértices
D3	Diedro trigonal				{3,2}	{3}			2	3	3
H3	Hosoedro trigonal				{2,3}			{2}	3	3	2
D6	Diedro trigonal truncado (como un diedro hexagonal)				t{3,2}	{6}			2	6	6
P3	Hosoedro trigonal truncado (Prisma triangular)				t{2,3}	{3}	{4}		5	9	6
P6	Diedro trigonal omnitruncado (Prisma hexagonal)				t0,1,2{2,3}=tr{2,3}	{6}	{4}	{4}	8	18	12
A3 [2]	Diedro trigonal achatado (como un antiprisma triangular) (como un octaedro)				sr{2,3}	{3}	2 {3}		8	12	6
P3	Diedro trigonal achatado canteado (Prisma triangular)				s2{2,3}=t{2,3}				5	9	6

Simetría diédrica (4 2 2) D_4h

Hay 16 triángulos fundamentales, visibles en las caras de la bipirámide octogonal y en los triángulos de colores alternados en una esfera:

#	Nombre	Imagen	Teselado	Figura de vértice	Símbolos de Coxeter y de Schläfli	Número de caras por posición			Número de elementos
						Pos. 2 [4] (2)	Pos. 1 [2] (4)	Pos. 0 [2] (4)	Caras	Aristas	Vértices
D4	Diedro cuadrado				{4,2}	{4}			2	4	4
H4	Hosoedro cuadrado				{2,4}			{2}	4	4	2
D8	Diedro cuadrado truncado (como un diedro octogonal)				t{4,2}	{8}			2	8	8
P4 [7]	Hosoedro cuadrado truncado (Cubo)				t{2,4}	{4}	{4}		6	12	8
D8	Diedro cuadrado omnitruncado (Prisma octogonal)				t0,1,2{2,4}=tr{2,4}	{8}	{4}	{4}	10	24	16
A4	Diedro cuadrado achatado (Antiprisma cuadrado)				sr{2,4}	{4}	2 {3}		10	16	8
P4 [7]	Diedro cuadrado achatado canteado (Cubo)				s2{4,2}=t{2,4}				6	12	8
A2 [1]	Hosoedro cuadrado achatado (Disfenoide) (Tetraedro)				s{2,4}=sr{2,2}				4	6	4

Simetría diédrica (5 2 2) D_5h

Hay 20 triángulos fundamentales, visibles en las caras de una bipirámide decagonal y en los triángulos de colores alternados en una esfera:

#	Nombre	Imagen	Teselado	Figura de vértice	Símbolos de Coxeter y de Schläfli	Número de caras por posición			Número de elementos
						Pos. 2 [5] (2)	Pos. 1 [2] (5)	Pos. 0 [2] (5)	Caras	Aristas	Vértices
D5	Diedro pentagonal				{5,2}	{5}			2	5	5
H5	Hosoedro pentagonal				{2,5}			{2}	5	5	2
D10	Diedro pentagonal truncado (como un diedro decagonal)				t{5,2}	{10}			2	10	10
P5	Hosoedro pentagonal truncado (como un prisma pentagonal)				t{2,5}	{5}	{4}		7	15	10
P10	Diedro pentagonal omnitruncado (Prisma decagonal)				t0,1,2{2,5}=tr{2,5}	{10}	{4}	{4}	12	30	20
A5	Diedro pentagonal achatado (Antiprisma pentagonal)				sr{2,5}	{5}	2 {3}		12	20	10
P5	Diedro pentagonal achatado canteado (Prisma pentagonal)				s2{5,2}=t{2,5}				7	15	10

Simetría diédrica (6 2 2) D_6h

Hay 24 triángulos fundamentales, visibles en las caras de una bipirámide dodecagonal y en los triángulos de colores alternados de una esfera.

#	Nombre	Imagen	Teselado	Figura de vértice	Símbolos de Coxeter y de Schläfli	Número de caras por posición			Número de elementos
						Pos. 2 [6] (2)	Pos. 1 [2] (6)	Pos. 0 [2] (6)	Caras	Aristas	Vértices
D6	Diedro hexagonal				{6,2}	{6}			2	6	6
H6	Hosoedro hexagonal				{2,6}			{2}	6	6	2
D12	Diedro hexagonal truncado (como un diedro dodecagonal)				t{6,2}	{12}			2	12	12
H6	Hosoedro hexagonal truncado (como un prisma hexagonal)				t{2,6}	{6}	{4}		8	18	12
P12	Diedro hexagonal omnitruncado (Prisma dodecagonal)				t0,1,2{2,6}=tr{2,6}	{12}	{4}	{4}	14	36	24
A6	Diedro hexagonal achatado (Antiprisma hexagonal)				sr{2,6}	{6}	2 {3}		14	24	12
P3	Diedro hexagonal canteado (Prisma triangular)				= h2{6,2}=t{2,3}				5	9	6
P6	Diedro hexagonal achatado canteado (Prisma hexagonal)				s2{6,2}=t{2,6}				8	18	12
A3 [2]	Hosoedro hexagonal achatado (como un antiprisma triangular) (como un octaedro)				s{2,6}=sr{2,3}				8	12	6

Operadores de construcción de Wythoff

Operación	Símbolo	Diagrama de Coxeter	Descripción
Relacionado	{p,q} t0{p,q}		Cualquier poliedro regular o teselado
Rectificado (r)	r{p,q} t1{p,q}		Las aristas originales están completamente truncadas, convertidas en puntos únicos. El nuevo poliedro presenta caras combinadas del original y del dual. Los poliedros se nombran por el número de lados de las dos formas regulares: {p, q} y {q, p}, como el cuboctaedro r {4,3}, a medias entre un cubo y un octaedro.
Birrectificado (2r) (también conjugado o dual)	2r{p,q} t2{p,q}		El birectificado (dual) es un truncamiento adicional, de forma que las caras originales se reduzcan a puntos. Se forman nuevas caras debajo de cada vértice original. El número de aristas no cambia, pero se gira 90 grados. Una birrectificación puede verse como el poliedro dual.
Truncado (t)	t{p,q} t0,1{p,q}		Cada vértice original se corta, generando una nueva cara bajo el mismo. El truncamiento tiene un grado de libertad, con una solución que crea un poliedro truncado uniforme. El poliedro mantiene sus caras originales pero con el número de aristas duplicado y contiene las caras del dual.
Bitruncado (2t) (también truncado dual)	2t{p,q} t1,2{p,q}		Un bitruncado puede verse como el truncamiento del poliedro dual. Un cubo bitruncado es un octaedro truncado.
Canteado (rr) (también expandido)	rr{p,q}		Además del truncamiento de vértices, cada arista original puede ser biselada formando nuevas caras rectangulares que aparecen en su lugar. Un canteado uniforme está a medio camino entre la forma original y la dual. Un poliedro canteado se nombra como rombi-r{p, q}, como por ejemplo, el rombicuboctaedro para rr{4,3}.
Canteado truncado (tr) (también omnitruncado)	tr{p,q} t0,1,2{p,q}		Las operaciones de truncamiento y canteado se aplican juntas para crear una forma omnitruncada que tiene las caras del original dobladas en las aristas, las caras del dual dobladas en las aristas y cuadrados donde se situaban las aristas originales.

Operaciones de alternado

Operación	Símbolo	Diagrama de Coxeter	Descripción
Rectificado achatado (sr)	sr{p,q}		Canteados truncados alternos. Todas las caras originales terminan con la mitad de aristas y los cuadrados degeneran en aristas. Dado que las formas omnitruncadas tienen 3 caras/vértice, se forman nuevos triángulos. Por lo general, estas formas de facetas alternas se deforman ligeramente a partir de entonces para terminar nuevamente como poliedros uniformes. La posibilidad de esta última variación depende del grado de libertad.
Achatado (s)	s{p,2q}		Truncado alternado
Achatado canteado (s2)	s2{p,2q}
Canteado alternado (hrr)	hrr{2p,2q}		Solo posible en teselaciones uniformes (poliedros infinitos), alternancia de Por ejemplo,
Mitad (h)	h{2p,q}		Alternación de , igual que
Canteado (h2)	h2{2p,q}		igual que
Mitad rectificada (hr)	hr{2p,2q}		Solo posible en teselaciones uniformes (poliedros infinitos), alternancia de , igual que o Por ejemplo, = o
Cuarto (q)	q{2p,2q}		Solo posible en teselaciones uniformes (poliedros infinitos), igual que Por ejamplo, = o

Véase también

• Poliedro
  • Poliedro regular
  • Poliedro cuasirregular
  • Poliedro semirregular
• Anexo:Poliedros uniformes
  • Anexo:Poliedros uniformes por figura de vértice
  • Anexo:Poliedros uniformes por símbolos de Wythoff
  • Anexo:Poliedros uniformes por el triángulo de Schwarz
• Anexo:Sólidos de Johnson
• Anexo:Modelos de poliedros de Wenninger
• Modelo de poliedro
• Teselado uniforme
• Teselados uniformes en el plano hiperbólico
• Poliedro pseudouniforme
• Anexo:Figuras geométricas