Kiirus

Kiirus ehk liikumiskiirus on füüsikaline suurus, mis näitab, kui palju ja mis suunas muutub liikuva keha või nähtuse asukoht ruumis ajaühiku jooksul. Füüsikas käsitatakse kiirust tavaliselt aja funktsioonina, mille väärtus antud hetkel on hetkkiirus.

See artikkel räägib liikumiskiirusest; ajast sõltuva suuruse muutumise kiiruse kohta vaata artiklit Muutumiskiirus

---

Kiirus on asukoha ja kiirenduse kõrval üks kinemaatika põhimõisteid.

Kiirus on vektoriaalne suurus, seega saab seda iseloomustada kiirusvektori pikkuse ehk mooduli ehk arvväärtusega ja liikumissuunaga (paigalseisu puhul on suund määramata).

Kiiruseks nimetatakse sageli ka kiirusvektori pikkust ehk moodulit ehk arvväärtust, mis on skalaarne suurus. See on näiteks auto sõidukiirus.

Kiiruse tähis on ${\displaystyle {\vec {v}}}$ (kiirusvektori pikkuse korral ${\displaystyle v}$), mis tuleb ladina keele sõnast velocitas kiirus.

Kiiruse (kiirusvektori pikkuse) SI mõõtühik on meeter sekundis (m/s ehk m·s^–1), dimensioon on L·T⁻¹. CGS-süsteemis on ühik cm·s⁻¹, dimensioon on L·T⁻¹. Plancki ühik on c, dimensioon on c. Laialt on kasutusel ka ühik kilomeeter tunnis (km/h), kusjuures 1 m/s = 3,6 km/h, samuti on eelkõige merenduses ja lennunduses kasutusel sõlm.

Suurim võimalik kiirus, millega kindla põhjuse tagajärg saab ruumis levida, on valguse kiirus ${\displaystyle c}$. See ülempiir kehtib järelikult ka igasuguse informatsiooni ülekande kohta. Kehad, millelon mass, saavad liikuda ainult kiirusest ${\displaystyle c}$ väiksema kiirusega.

Kiiruse väärtust tuleb alati mõista mingi taustsüsteemi suhtes. Kui keha seisab mingis taustsüsteemis paigal, siis tal on mingis teises taustsüsteemis, mis liigub esimese suhtes kiirusega ${\displaystyle {\vec {v}}}$, kiirus ${\displaystyle -{\vec {v}}}$.

Definitsioon

Trajektoor (sinine), kohavektorid (${\displaystyle {\vec {r}}_{\mathrm {A} }}$, ${\displaystyle {\vec {r}}_{\mathrm {B} }}$), kõõl (${\displaystyle \Delta {\vec {r}}}$) ja teepikkus (trajektoori osa pikkus ${\displaystyle A}$-st ${\displaystyle B}$-ni)

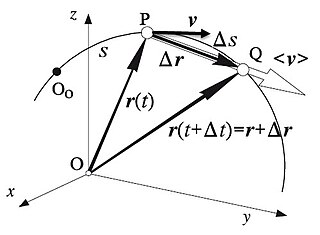
Kui punktmassina vaadeldav objekt liigub mööda trajektoori, kusjuures ta asub hetkel ${\displaystyle t}$ punktis ${\displaystyle A}$ ja hilisemal hetkel ${\displaystyle t+\Delta t}$ punktis ${\displaystyle B}$, siis tema kiiruse lähendväärtus ${\displaystyle {\vec {v}}(t)}$ hetkel ${\displaystyle t}$ (või punktis ${\displaystyle A}$) saadakse kohavektori muudust ${\displaystyle \Delta {\vec {r}}}$ ja kohavahetuseks vajalikust ajavahemikust ${\displaystyle \Delta t}$ valemiga

${\displaystyle {\vec {v}}(t)\approx {\frac {\Delta {\vec {r}}}{\Delta t}},}$

kus ${\displaystyle \Delta {\vec {r}}={\vec {r}}(t+\Delta t)-{\vec {r}}(t)={\vec {r}}_{B}-{\vec {r}}_{A}}$ on vektor punktist ${\displaystyle A}$ punkti ${\displaystyle B}$. Geomeetriliselt vastab see trajektooriosa kõõlule nende kahe pu vahel. See lähendväärtus annab ka kiiruse suuna lähendi. Sellest lähendväärtusest saadakse hetkkiiruse täpne definitsioon hetkel ${\displaystyle t}$ (või punktis ${\displaystyle A}$), kui ajavahemikul ${\displaystyle \Delta t}$ lastakse läheneda nullile. Seejuures jõuab punkt ${\displaystyle B}$ (liikumise pidevuse põhjal) punktile ${\displaystyle A}$ kui tahes lähedale, nii et ka ${\displaystyle \Delta {\vec {r}}}$ läheneb nullile; jagatis ${\displaystyle {\tfrac {\Delta {\vec {r}}}{\Delta t}}}$ aga läheneb piirväärtusele, mis vastabki hetkkiirusele:

${\displaystyle {\vec {v}}(t)=\lim _{\Delta t\rightarrow 0}{\frac {{\vec {r}}(t+\Delta t)-{\vec {r}}(t)}{\Delta t}}.}$

Teepikkused kõverjoonelise liikumise korral

Sirgliikumise juhtum

See kirjutatakse ka nii

${\displaystyle {\vec {v}}(t)={\frac {\mathrm {d} {\vec {r}}}{\mathrm {d} t}}\quad }$ või ${\displaystyle \quad {\vec {v}}(t)={\dot {\vec {r}}}}$,

sest tegu on tuletisega aja järgi.

Et kõõl ${\displaystyle \Delta {\vec {r}}}$ võtab piirprotsessis trajektoori puutuja suuna, on see ka hetkkiiruse suund.

Hetkkiirusvektori pikkus on antud valemiga

${\displaystyle v=\left|{\vec {v}}\right|=\left|\lim _{\Delta t\rightarrow 0}{\frac {\Delta {\vec {r}}}{\Delta t}}\right|=\left|{\frac {\mathrm {d} {\vec {r}}}{\mathrm {d} t}}\right|=\left|{\dot {\vec {r}}}\right|,}$

kus ${\displaystyle \left|{\vec {r}}\right|=r}$ on kohavektori ${\displaystyle {\vec {r}}}$ pikkus. Hetkkiirusvektori pikkus ei ole sama mis ${\displaystyle \left|{\dot {r}}\right|}$, nagu on näha näiteks ringliikumise puhul, kus ${\displaystyle r={\text{konst.}},\ v\neq 0,\ {\dot {r}}=0}$.

Hetkkiirusvektori pikkus on võimalik saada ka, kui võtta kolmemõõtmelise trajektoori asemel ainult teepikkus ${\displaystyle s}$) mööda trajektoori (vt joonist). Sel juhul võetakse läbitud teepikkuse ${\displaystyle \Delta s}$ ja kulunud aja piirväärtus ${\displaystyle \Delta t}$:

${\displaystyle v=\lim _{\Delta t\rightarrow 0}{\frac {\Delta s}{\Delta t}}={\frac {\mathrm {d} s}{\mathrm {d} t}}={\dot {s}}.}$

Keskmine kiirus <v> ja hetkkiirus ${\displaystyle v}$

Keskmine kiirus

Vaata ka: Keskmine kiirus

Keskmine kiirus ${\displaystyle v_{k}}$, on keha läbitud teepikkuse ${\displaystyle \Delta s}$ ja selleks kulunud aja ${\displaystyle \Delta t}$ jagatis

${\displaystyle v_{k}={\frac {\Delta s}{\Delta t}}}$.

Lihtsad erijuhtumid

Ühtlane sirgliikumine

Ühtlane sirgliikumine ehk ühtlane liikumine on olukord, kus objekti kiirus ${\displaystyle {\vec {v}}}$ on alati ühesugune (st nii arvväärtuse kui ka suuna poolest), ehk teisiti öeldes, ${\displaystyle {\vec {a}}(t)={\vec {0}}}$. Sel juhtumil liigub objekt mööda sirget, millele tavaliselt rihitakse koordinaadistik, nii et kiirus on skalaarne suurus ${\displaystyle v}$. Siis kehtib:

${\displaystyle v={\frac {s}{t}},}$

kus ${\displaystyle s}$ on aja ${\displaystyle t}$ jooksul läbitud teepikkus.

Ühtlaselt kiirenev liikumine

Vaata ka: Ühtlaselt kiirenev liikumine

Ühtlaselt kiireneva liikumise korral on kiirendusel ${\displaystyle {\vec {a}}}$ alati sama arvväärtus ja sama suund. Kui liikumise suund on kiirendusega ${\displaystyle {\vec {a}}}$ paralleelne, siis liigub objekt mööda sirget. Praktiselt rihitakse koordinaadistik liikumise suunale ning kujutatakse kiirendust ja kiirust skalaarina. Siis kehtib

${\displaystyle v(t)=a\cdot t+v_{0},}$

kus ${\displaystyle {v}_{0}}$ on algkiirus.

Ringliikumine

 Pikemalt artiklis Ringliikumine

Ringliikumise kiirus on nurkkiiruse ja ringliikumise raadiusvektori vektorkorrutis:

${\displaystyle {\vec {v}}={\vec {\omega }}\times {\vec {r}},}$

kus ${\displaystyle \omega }$ on nurkkiirus ja ${\displaystyle r}$ on raadiusvektor.

Ühtlase ringliikumise korral on ringlikumise arvväärtus konstantne ja seda saab avaldada ringjoonel läbitud teepikkuse ja selleks kulunud aja ${\displaystyle T}$ jagatisena:

${\displaystyle v={\frac {2\cdot \pi \cdot r}{T}}.}$

Seosed teiste füüsikaliste suurustega

Seos asukohaga

Kui punktmass liigub ruumis (kolmemõõtmeline ruum), siis saab kiirusvektori ${\displaystyle {\vec {v}}}$ ajalisest kulust järeldada punktmassi siirde, integreerides ${\displaystyle {\vec {v}}}$ üle aja:

${\displaystyle {\vec {r}}_{2}-{\vec {r}}_{1}=\int _{t_{1}}^{t_{2}}{\vec {v}}(t)\,\mathrm {d} t}$,

kus ${\displaystyle {\vec {r}}_{2}={\vec {r}}(t_{2})}$ ja ${\displaystyle {\vec {r}}_{1}={\vec {r}}(t_{1})}$. Siit saab avaldada punktmassi asukoha lõpphetkel:

${\displaystyle {\vec {r}}_{2}={\vec {r}}_{1}+\int _{t_{1}}^{t_{2}}{\vec {v}}(t)\,\mathrm {d} t}$.

Kui punktmass liigub mööda sirget (sirgliikumine, ühemõõtmeline liikumine), siis rihitakse koordinaadistik tavaliselt sellele sirgele. Osakese asukohta kirjeldatakse siis ainult koordinaadiga ${\displaystyle x=x(t)}$. Ülaltoodud valem lihtsustub sel juhtumil valemiks

${\displaystyle x_{2}-x_{1}=\int _{t_{1}}^{t_{2}}v(t)\,\mathrm {d} t}$.

See on Newtoni-Leibnizi teoreemi kinemaatiline versioon.

Seos teepikkusega

Läbitud teepikkus ${\displaystyle s}$ saadakse kiirusvektori arvväärtuse ${\displaystyle |{\vec {v}}|}$ integreerimisel üle aja:

${\displaystyle s=\int _{t_{1}}^{t_{2}}|{\vec {v}}(t)|\,\mathrm {d} t}$.

Lihtsaimal juhul, nimelt konstantse kiiruse korral, saab sellest ${\displaystyle s=v\cdot (t_{2}-t_{1})}$.

Seos kiirendusega ja kiirenduse muutumise kiirusega

Kiiruse esimene tuletis aja järgi on kiirendus: ${\displaystyle {\vec {a}}(t)={\dot {\vec {v}}}(t)={\ddot {\vec {r}}}(t)}$.

Kiirus saadakse kiirendusest integreerimisel:

${\displaystyle {\vec {v}}(t)={\vec {v}}_{0}+\int _{0}^{t}{\vec {a}}(\tau )\,\mathrm {d} \tau }$.

Kui liikumine leiab aset sirgel, siis rihitakse koordinaadistik praktiliselt liikumise suunas ning saadakse skalaarne võrrand

${\displaystyle v(t)=v_{0}+\int _{0}^{t}a(\tau )\,\mathrm {d} \tau }$.

Kiiruse teine tuletis aja järgi annab kiirenduse muutumise kiiruse: ${\displaystyle {\vec {j}}(t)={\ddot {\vec {v}}}(t)={\dot {\vec {a}}}(t)}$. Kiirus saadakse kiirenduse muutumise kiirusest kahe integreerimisega.

Seos impulsi ja kineetilise energiaga

Massiga ${\displaystyle m}$ keha impulss arvutatakse valemiga ${\displaystyle {\vec {p}}=m\cdot {\vec {v}}}$, kineetiline energia on antud valemiga ${\displaystyle E_{\mathrm {kin} }={\tfrac {1}{2}}mv^{2}={\tfrac {p^{2}}{2m}}}$.

Rangelt võttes kehtivad need võrrandid üksnes ligikaudselt nn mitterelativistlikul juhtumil, st kiiruste korral, mis on valguse kiirusest palju väiksemad.

Mõõtmine

 Pikemalt artiklis Kiiruse mõõtmine

Kõige lihtsam viis kiirust määrata on mõõta,

• kui palju aega läheb teatud kindla teepikkuse läbimiseks või
• kui pikk tee läbitakse antud ajavahemikus.

Mõlemal juhul mõõdetakse õigupoolest ainult keskmist kiirust. Kui aga teelõik või ajavahemik valitakse piisavalt lühike või liikumine on ligikaudu ühtlane, siis on mõlema meetodiga võimalik jõuda rahuldava täpsuseni. Üks näide esimesest meetodist on Hippolyte Fizeau hammasrattameetod valguse kiiruse mõõtmiseks. Teist meetodit kasutatakse muu hulgas siis, kui kiiruse väärtusi arvutatakse GPSi andmete põhjal.

Ratastega sõiduki sõidukiirust on kerge määrata spidomeetri abil. See möödab õigupoolest ratta pöörlemissagedust, mis on kiirusega võrdeline.

Mõõtmismeetodina on aga võimalik kasutada praktiliselt kõiki kiirusest sõltuvaid efekte, nii näiteks Doppleri efekti Doppleri radaris, impulssi ballistilises pendlis ja kiirusrõhku Prandtli torus.

Ühikud

Kiiruse SI ühik on meeter sekundis (m/s). Teine laialt kasutatav kiirusühik on kilomeeter tunnis (km/h).

Ameerika Ühendriikides ja mõnedes teistes ingliskeelsetes maades on kasutusel miil tunnis (mph). Merenduses ja lennunduses on kasutusel sõlm (meremiil tunnis). Vertikaalkiirusi esitatakse motoriseeritud lennunduses sageli jalgades minutis (LFM (linear feet per minute), fpm (feet per minute)).

Peaaegu ainult lennunduses kasutatakse Machi arvu, vaid kiiruse suhte lokaalse helikiirusega. Helikiirus sõltub oluliselt temperatuurist, kuid mitte õhurõhust. Seda arvu kasutatakse sellepärast, et sellest sõltuvad aerodünaamilised efektid.

Käibel olevate kiirusühikute teisendamine:

	Meetrit sekundis	Kilomeetrit tunnis	Sõlme (meremiili tunnis)	Miili tunnis	Valguse kiirust
1 m/s	00 1	00 3,6	00 1,944	00 2,237	0 3,336 · 10−9
1 km/h	00 0,2778	00 1	00 0,5400	00 0,6215	0 9,266 · 10−10
1 sõlm	00 0,5144	00 1,852	00 1	00 1,151	0 1,716 · 10−9
1 mph	00 0,4469	00 1,609	00 0,8688	00 1	0 1,491· 10−9
1 ${\displaystyle c}$	00 299792458	00 1,079 · 109	00 5,827 · 108	00 6,707 · 108	00 1

Märkus: rasvases kirjas esitatud teisendustegurid on täpsed, kõik teised tegurid on ümardatud neljale tüvenumbrile.

Kiirused ja taustsüsteem

Möödalendav lennuk kiirusega (punane), radiaalkiirusega (roheline) ja tangentsiaalkiirusega (sinine)

Vastavalt taustsüsteemile või koordinaadistikule on kujunenud erinevad nimetused.

Vertikaal- ja horisontaalkiirused

Homogeense raskusvälja puhul kasutatakse sageli Descartesi koordinaate. Kiirusi, mis on raskuskiirendusega ${\displaystyle {\vec {g}}}$ kollineaarsed, nimetatakse enamasti vertikaalkiirusteks, kiirusi, mis on raskuskiirendusega ortogonaalsed, nimetatakse horisontaalkiirusteks.

Radiaalkiirus, tangentsiaalkiirus ja ringikiirus

Polaarkoordinaatide puhul on radiaalkiirus ${\displaystyle {\vec {v}}_{\mathrm {r} }}$ kiirusvektori komponent kohavektori sihis, st piki liikuvat objekti ja koordinaatide alguspunkti ühendavat kiirt. Sellega risti olevat komponenti nimetatakse ringikiiruseks S${\displaystyle {\vec {v}}_{\perp }}$. Nii saame: ${\displaystyle {\vec {v}}={\vec {v}}_{\perp }+{\vec {v}}_{\mathrm {r} }}$. Nurkkiiruse ja kohavektori vektorkorrutis annab ringikiiruse: ${\displaystyle {\vec {v}}_{\perp }={\vec {\omega }}\times {\vec {r}}}$.

Liikumiste korral mööda ringjoont, mille keskpunkt on koordinaatide alguspunkt, ja ka ainult sel juhtumil, on radiaalkiirus null ja ringikiirus võrdub tangentsiaalkiirusega, st kiirusega piki trajektoori puutujat.

Sellest, et kaugus koordinaatide alguspunktist (raadius) muutub, tuleneb radiaalkiirus: ${\displaystyle {\vec {v}}_{\mathrm {r} }={\dot {r}}\,{\frac {\vec {r}}{|{\vec {r}}|}}}$.

Absoluutne kiirus ja suhteline kiirus

Eeldusel, et on olemas üldkehtiv taustsüsteem, nimetatakse selles süsteemis mõõdetavaid kiirusi absoluutseteks kiirusteks. Kiirusi punkti suhtes, mis ise selles punktis liigub, nimetatakse suhtelisteks kiirusteks. Näide: tramm liigub kiirusega 50 km/h. Selles liigub piki trammi sõitja suhtelise kiirusega (trammi suhtes) kiirusega 5 km/h. Tema absoluutne kiirus (tänaval seisva vaatleja suhtes) on järelikult 55 km/h või 45 km/h vastavalt sellele, kas ta liigub sõidusuunas või vastu sõidusuunda.

Ent relatiivsusprintsiip ütleb, et ei ole füüsikalist alust, miks peaks mõnd kindlat taustsüsteemi kõigile teistele eelistama. Kõik füüsikaseadused, mis kehtivad ühes inertsiaalsüsteemis, kehtivad ka kõigis teistes inertsiaalsüsteemides. See, milliseid liikumisi peetakse absoluutseteks, on niisiis täiesti suvaline. Hiljemalt erirelatiivsusteooriast saadik sellepärast absoluutse kiiruse mõistet välditakse. Sellepärast on kõik kiirused suhtelised kiirused. Sellest relatiivsusprintsiibist koos sellega, et valguse kiirus on invariantne (Lorentzi invariant) järeldub, et kiirusi ei saa lihtsalt liita, nagu ülaltoodud näites vaikimisi eeldati. Selleasemel kehtib relativistlik kiiruste liitmise teoreem. See saab aga märgatavaks alles väga suurte kiiruste korral.

Näide: suhteline kiirus astronoomias

Näide astronoomiast illustreerib seda, et absoluutne kiirus ei mängi mingit rolli, sest absoluutselt paigalseisvat taustsüsteemi ei ole põhimõtteliselt olemas. Koordinaattelgedel on tähistaeva suhtes kindel suund, taustsüsteem seisab mingis raskuskeskmes paigal. Siis Kuu kiirus:

Kuu kiirus

	Keskmine orbitaalkiirus (ümber Maa ja Kuu raskuskeskme)	ümber Päikese või Päikesesüsteemi raskuskeskme	ümber Linnutee galaktika (galaktiline aasta)	Andromeeda galaktika suhtes
Kiirus (km/s)	1,02 ± 5,5 % kuu jooksul	29,78 ± 1,51 (±5,1% aasta jooksul)	umbes 250 (igal galaktilisel aastal, täpsed kõikumised teadmata)	266 ± 31,3 (aasta jooksul)
Keskmise orbitaalkiiruse osatähtsus keskmises suhtelises kiiruses	100%	3,4%	0,4%	0,37%

Universumi kaugete objektide puhul määrab kiiruse primaarselt aegruumi paisumine, ja seda mõõdetakse näiteks punanihke kaudu.

Arvukate osakeste kiirus

Dilämmastiku molekulide kiiruste jaotuse sõltuvus temperatuurist

Paljudest osakestest koosneva süsteemi puhul ei ole enamasti enam mõttekas või üldse võimalik anda iga üksiku molekuli kiirust. Selleasemel töötatakse kiirusjaotusega, mis näitab, kui sageli kiiruste teatav vahemik osakeste ansamblis esineb. Näiteks ideaalses gaasis kehtib Maxwelli-Boltzmanni jaotus ehk Maxwelli jaotus (vt joonist): enamiku osakeste kiirus on lähedane kõige tõenäosemale kiirusele, mida näitab Maxwelli-Boltzmanni jaotuse maksimum. Esineb ka väga väikesi ja väga suuri kiirusi, aga eeldatavalt on need päris vähestel osakestel. Maksimum sõltub temperatuurist. Mida kuumem gaas on, seda suurem on kõige tõenäosem kiirus. Rohkematel osakestel on siis suur kiirus. See näitab, et teperatuur on osakeste keskmise kineetilise energia mõõt. Siiski ei ole ka madalatel temperatuuridel väga suured kiirused välistatud. Kiirusjaotusega on seletatavad paljud füüsikalised transpordinähtused, nagu näites difusioon gaasides.

Voolise voolukiirus

 Pikemalt artiklis Voolukiirus

Vaata ka: Vooluväli

Gaasi või vedeliku keskmine voolukiirus ${\displaystyle v_{\mathrm {A} }}$ saadakse mahtvooluhulgast ${\displaystyle Q={\tfrac {\mathrm {d} V}{\mathrm {d} t}}}$ voolu ristlõike pindala ${\displaystyle A}$ kaudu:

${\displaystyle v_{\mathrm {A} }={\frac {Q}{A}}}$

Lokaalsed voolukiirused aga võivad üksteisest väga palju erineda. Näiteks on kiirus ideaalse toru keskel kõige suurem ja langeb hõõrdumise tõttu toru seina juures nullini. Sellepärast tuleb keskkonna voolamist käsitada vektorväljana. Kui kiirusvektorid on ajas konstantsed, siis räägitakse muutumatust voolamisest. Kui aga kiirused käituvad kaootiliselt, siis on tegu turbulentse voolamisega. Voolamiskäitumist aitab iseloomustada Reynoldsi arv, mis seob voolukiiruse vooluga kokkupuutuva keha mõõtmetega ja voolise viskoossusega.

Matemaatiliselt modelleeritakse kiiruste käitumist Navier'-Stokesi võrranditega, mis diferentsiaalvõrranditena seovad kiirusvektoreid sise- ja välisjõududega. Sellega on neil voolise liikumise jaoks sarnane tähtsus nagu mehaanika põhivõrrandil (Newtoni teisel seadusel punktmasside ja jäikade kehade jaoks.

Lainete kiirus

8Punane punkt liigub faasikiirusega ja rohelised punktid rühmakiirusega

 Pikemalt artiklites Laine levimiskiirus, Osakese kiirus, Faasikiirus ja Rühmakiirus

Lainete liikumise keerukuse tõttu tuleb kasutada erinevaid kiirusemõisteid. (Ka laine levimiskiirus võib tähendada eri asju.)

• Mehaaniliste lainete osakese kiirus näitab, kui kiiresti keskkonna osakesed tasakaaluolekust välja liiguvad. Tuntuim näide on õhuosakeste võnkumiskiirus helilaines.
• Kiirust, millega mingi kindla faasi punkt edasi liigub, nimetatakse faasikiiruseks. Kehtib seos: ${\displaystyle v_{\mathrm {p} }={\frac {\lambda }{T}}={\frac {\omega }{k}}}$, kus ${\displaystyle \lambda }$ on lainepikkus, ${\displaystyle T}$ laine periood, ${\displaystyle \omega }$ ringsagedus ja ${\displaystyle k}$ ringlainearv. Kiirus, millega liiguvad laineharjad meres, on faasikiiruse tüüpiline näide.
• Kiirust, millega liigub terve lainepakett, nimetatakse rühmakiiruseks: ${\displaystyle v_{\mathrm {g} }={\frac {\partial \mathbf {\omega } }{\partial \mathbf {k} }}}$.

Faasi- ja rühmakiirus langevad kokku üksnes harvadel juhtudel (näiteks valguse levimise korral vaakumis). Reeglina need erinevad. Üks näitlik äärmuslik näide on madude kulgemine: kui käsitada madu lainena, siis tema edasijõudmise kiirus on rühmakiirus. Faasikiirus siuglemisel on aga null, sest kohad, kus mao keha kõverdub paremale või vasakule, on pinnaga ette antud ega liigu mööda maapinda.

Reeglina sõltub füüsikalise laine faasikiirus sagedusest või ringlainearvust. Seda efekti nimetatakse dispersiooniks. Dispersiooni tõttu murdub näiteks eri lainepikkusega valgus prismal erineval määral.

Relatiivsusteooria

 Pikemalt artiklis Erirelatiivsusteooria

Klassikalise füüsika seadustest järeldub kiiruste kohta muu hulgas:

• Pikkuste ja aegade mõõtarvud on sõltumatud vaatleja liikumisolekust, sealhulgas kiirusest. Muu hulgas on kõik vaatlejad ühel meelel selles, kas kaks sündmust toimuvad üheaegselt.
• Taustsüsteemi vahetamisel kehtib Galilei teisendus. See tähendab, et keha liikumise kiirust mingis taustsüsteemis ja selle taustüsteemi liikumise kiirust teise taustsüsteemi suhtes tohib vektoriaalselt liita, et saada keha iikumise kiirus teises taustsüsteemi.
• Liikumiste kiirusel ei ole teoreetilist ülempiiri.

Kuigi klassikalise füüsika seadused seda ei nõua, eeldati enne Einsteiniüldiselt, et on olemas kõikide kiiruste universaalne taustsüsteem – eeter. Kui see oleks nii, peaks elektromagnetlainete levimiskiirus sõltuma vastuvõtja liikumisolekust.

Michelsoni-Morley eksperiment ei kinnitanud viimast sõltuvust. Einstein postuleeris, et relatiivsusprintsiipi, mis oli teada juba klassikalisest mehaanikast, tuleb rakendada ka kõigile teistele füüsikanähtustele, sealhulgas valguse levimisele, ning et valguse kiirus on sõltumatu saatja liikumisolekust. Sellest tegi ta järelduse, et ülaltoodud klassikalise mehaanika väiteid tuleb modifitseerida.^[1] Üksikasjades tähendab see:

• Pikkuste ja aegade mõõtarvud sõltuvad vaatleja liikumisolekust, sealhulgas kiirusest (vt aja dilatatsioon ja pikkuse kontraktsioon ehk Lorentzi kontraktsioon). Ka üheaegsus on suhteline.
• Taustsüsteemi vahetamisel kehtib kehtib Lorentzi teisendus. See tähendab, et korraga toimuvate liikumiste kiirusi ei tohi lihtsalt vektoriaalselt liita.
• Kehad saavad liikuda ainult valguse kiirusest väiksema kiirusega. Ka informatsiooni ei saa üle kanda valguse kiirusest kiiremini.
• "Eetrit" ei olemas.

Erirelatiivsusteooriast tulenevad efektid saavad siiski märgatavaks alles väga suurte kiiruste korral. Lorentzi tegur, mis on aja dilatatsiooni ja pikkuse kontraktsiooni korral mõõduandev, annab alles ${\displaystyle v>4{,}2\cdot 10^{7}\,\mathrm {\tfrac {m}{s}} }$ korral ühest protsendist suurema hälbe. Järelikult on klassikaline mehaanika isegi kõige kiiremate seni valmistatud kosmoseaparaatide puhul äärmiselt täpne lähendus.

Uurimislugu

Visatava kivi liikumise kaks staadiumi Avicenna järgi: lõik АВ on "vägivaldse püüdluse periood", lõik ВС on "loomuliku püüdluse periood (langemine vertikaalselt allapoole)

Autolykos Pitanest defineeris 4. sajandil eKr ühtlase liikumise nii: "Punkti kohta öeldakse, et ta vahetab ühtlasel kohta, kui ta võrdsete aegadega läbib ühesugused suurused." Olgugi et definitsioonis osalesid nii teepikkus kui ka aeg, peeti nende suhet mõttetuks^[2], sest võrrelda sai ainult ühesuguseid suurusi, ja liikumise kiirus oli puhtkvalitatiivne, mitte kvantitatiivne mõiste^[3]. Samal ajal elanud Aristoteles jagas liikumise "loomulikuks", kui keha püüab jõuda oma "loomulikku" asukohta, ja "vägivaldseks", mis toimub jõu toimel. "Vägivaldse" liikumise puhul võrdub "liikumapanija" suuruse ja liikumise aja korrutis "liikumapandava" suuruse ja läbitud teepikkuse korrutisega, mis vastab valemile ${\displaystyle Ft=ms}$ või ${\displaystyle F=mv}$^[4]. Neidsamu vaateid jagasid Avicenna 11. sajandil, kellel oli küll teine arvamus liikumise põhjuste kohta^[5], ja Gerard Brüsselist 12. sajandi lõpus ja 13. sajandi alguses. Gerard kirjutas traktaadi "Liber de motu" ("Raamat liikumisest"), esimese ladinakeelse traktaadi kinemaatikast, milles ta sõnastas idee keha liikumise keskmise kiiruse määramisest (pöörlemisel liigub pöörlemisteljega paralleelne sirge "ühtemoodi mis tahes oma punktiga" ja raadius "ühtemoodi oma keskpunktiga")^[6].

1328. aastal ilmus Thomas Bradwardine'i "Traktaat proportsioonidest ehk kiiruste proportsioonidest liikumisel", milles ta leidis mittevastavuse Aristotelese füüsikas ja kiiruse seosed mõjuvate jõududega. Bradwardine märkis, et Aristotelese vormeli järgi kui liikumapanev jõud võrdub vastupanuga, siis kiirus on 1, kuna aga see peab olema 0. Ta esitas ka oma kiiruse muutumise vormeli, mis ei olnud küll füüsika seisukohast põhjendatud, kuid kujutas endast esimest kiiruse funktsionaalset sõltuvust liikumise põhjustest. Bradwardine nimetas kiirust liikumishulgaks^[7]. William Heytesbury võttis traktaadis "Kohalikust liikumisest" kasutusele hetkkiiruse mõistest. 1330ndatel ja 1340ndatel tõestasid tema ja teised Bradwardine'i õpilased nn Mertoni reegli, mis tähendab teepikkuse võrdsust ühtlaselt kiireneva liikumise ja keskmise kiirusega ühtlase liikumise puhul^[8].

Kiiruse mõistmise raskustest antiik- ja keskajal annavad tunnistust Zenoni apooriad "Achilleus ja kilpkonn" ja "Nool".

Kiiruse mõistesse tõi selgust Galileo Galilei. See märgistab läbimurret uusaegse füüsika suunas 17. sajandi alguses.^[9] Seni oli olnud täpselt defineeritud ainult keskmine kiirus antud lõplikul teel ning kiiruse suurenemist, nagu näiteks vaba langemise puhul, oli kujutatud kiiruse väikeste hüpete jadana. Galilei aga katab pidevalt muutuv kiirus kõikide vahepealsete väärtuste kontiinumi. Ta ei käsitanud vahepealseid väärtusi mitte keskmiste kiirustena tee tükikestel, vaid hetkkiirustena trajektoori punktides. Selle kiirusemõiste esitas piirprotsessi abil lõpmata väikestele teepikkustele täpselt alles Isaac Newton 17. sajandi lõpus.

Kiiruse arvväärtust ja suunda käsitleti algul lahus, kuni need 19. sajandil ühendati kiirusvektorina üheks matemaatiliseks suuruseks.

Liikumiskiirusi looduses ja tehnikas

Valguse kiirus	299 792 458 m/s
Kaugeimate galaktikate kiirus	${\displaystyle 1{,}4\times 10^{8}}$ m/s
Päikese kiirus tiirlemisel ümber Galaktika keskme	${\displaystyle 2{,}3\times 10^{5}}$ m/s
Maa kiirus tiirlemisel ümber Päikese	${\displaystyle 3{,}0\times 10^{4}}$ m/s
Maa tehiskaaslase kiirus	${\displaystyle 8000}$ m/s
Kuu kiirus tiirlemisel ümber Maa	${\displaystyle 1000}$ m/s
Reaktiivlennuki suurim kiirus	${\displaystyle 700}$ m/s
Lämmastiku molekuli keskmine kiirus 0 °C juures	${\displaystyle 500}$ m/s
Auto suurim kiirus	${\displaystyle 280}$ m/s
Kotka suurim lennukiirus	${\displaystyle 100}$ m/s
Gepardi kiirus	${\displaystyle 31}$ m/s
Inimese kiirus 100 m rekordjooksul	${\displaystyle 10}$ m/s
Inimese rekordkiirus 50 km käimisel	${\displaystyle 3{,}4}$ m/s
Kilpkonna kiirus	${\displaystyle 0{,}05}$ m/s
Teo kiirus	${\displaystyle 0{,}014}$ m/s

Vaata ka

• Algkiirus
• Liikumine
• Laine levimiskiirus
• Nurkkiirus
• Joonkiirus