Logaritmo complexo

En matemáticas, un logaritmo complexo é unha xeneralización do logaritmo natural aos números complexos non nulos. O termo pode referirse a un dos seguintes conceptos, que están estreitamente relacionados:

• Un logaritmo complexo dun número complexo non nulo ${\displaystyle z}$, definido como calquera número complexo ${\displaystyle w}$ tal que ${\displaystyle e^{w}=z}$.^[1][2] Tal número ${\displaystyle w}$ denótase por ${\displaystyle \log z}$.^[1] Se ${\displaystyle z}$ se expresa en forma polar como ${\displaystyle z=re^{i\theta }}$, onde ${\displaystyle r}$ e ${\displaystyle \theta }$ son números reais con ${\displaystyle r>0}$, entón ${\displaystyle \ln r+i\theta }$ é un logaritmo de ${\displaystyle z}$, e todos os logaritmos complexos de ${\displaystyle z}$ son exactamente os números da forma ${\displaystyle \ln r+i\left(\theta +2\pi k\right)}$, para enteiros ${\displaystyle k}$.^[1][2] Estes logaritmos están equidistantes ao longo dunha liña vertical no plano complexo.

• Unha función con valores complexos ${\displaystyle \log \colon U\to \mathbb {C} }$, definida nun subconxunto ${\displaystyle U}$ do conxunto ${\displaystyle \mathbb {C} ^{*}}$ dos números complexos non nulos, e que cumpre ${\displaystyle e^{\log z}=z}$ para todo ${\displaystyle z}$ en ${\displaystyle U}$. Tales funcións logarítmicas complexas son análogas á función logarítmica natural real ${\displaystyle \ln \colon \mathbb {R} _{>0}\to \mathbb {R} }$, que é a función inversa da función exponencial real e cumpre e^{ln x} = x para todo número real positivo x. As funcións logarítmicas complexas poden construírse mediante fórmulas explícitas que empregan funcións reais, por integración de ${\displaystyle 1/z}$, ou mediante o proceso de prolongamento analítico.

Unha rama do logaritmo complexo. O ton da cor úsase para amosar o argumento do logaritmo complexo. O brillo da cor úsase para amosar o módulo do logaritmo complexo.

. A súa gráfica obtense rotando a gráfica de ln(x) ao redor do eixo OZ.

Non existe ningunha función continua logarítmica complexa definida en todo ${\displaystyle \mathbb {C} ^{*}}$. As maneiras de tratar esta cuestión inclúen o uso de ramas, a superficie de Riemann asociada e as inversas parciais da función exponencial complexa. O valor principal define unha función logarítmica complexa particular ${\displaystyle \operatorname {Log} \colon \mathbb {C} ^{*}\to \mathbb {C} }$ que é continua agás ao longo do eixe real negativo; no plano complexo cos números reais negativos e o cero eliminados, constitúe o prolongamento analítico do logaritmo natural (real).

Problemas coa inversión da función exponencial complexa

Un gráfico da parte imaxinaria multivalorada da función logaritmo complexo, que mostra as ramas. Cando un número complexo z dá a volta arredor da orixe, a parte imaxinaria do logaritmo sobe ou baixa. Isto fai que a orixe sexa un punto de ramificación da función.

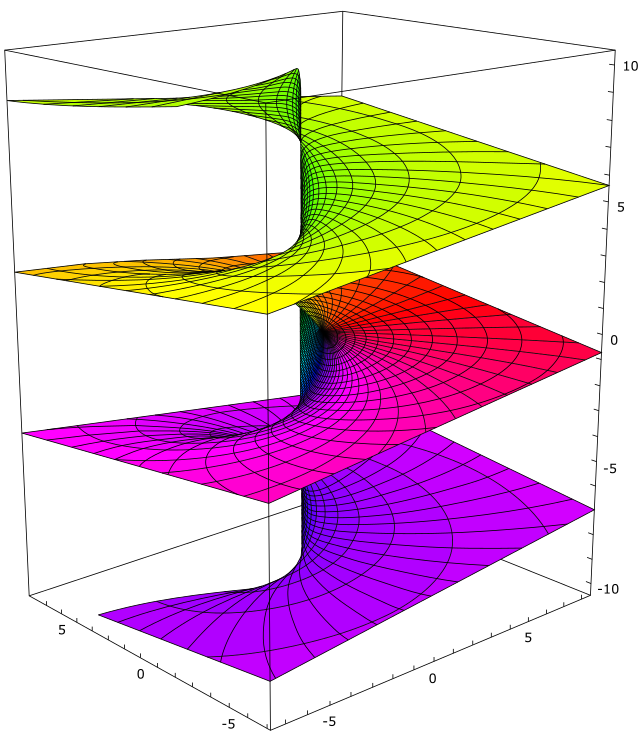
Para que unha función teña unha inversa, debe levar valores distintos a valores distintos; é dicir, debe ser inxectiva. Mais a función exponencial complexa non é inxectiva, porque ${\displaystyle e^{w+2\pi ik}=e^{w}}$ para todo número complexo ${\displaystyle w}$ e todo enteiro ${\displaystyle k}$, xa que engadir ${\displaystyle i\theta }$ a ${\displaystyle z}$ ten o efecto de rotar ${\displaystyle e^{w}}$ no sentido antihorario un ángulo ${\displaystyle \theta }$ en radiáns. Así, os puntos

${\displaystyle \ldots ,\;w-4\pi i,\;w-2\pi i,\;w,\;w+2\pi i,\;w+4\pi i,\;\ldots ,}$

equidistantes ao longo dunha liña vertical, todos se envían ao mesmo número pola función exponencial. Isto significa que a función exponencial non ten unha función inversa no sentido estándar.^[3][4] Existen dúas solucións a este problema.

Unha é restrinxir o dominio da función exponencial a unha rexión que non conteña dous números que difiran en múltiplos enteiros de ${\displaystyle 2\pi i}$: isto leva naturalmente á definición das ramas de ${\displaystyle \log z}$, que son certas funcións que escollen un logaritmo de cada número nos seus dominios. Isto é análogo á definición de ${\displaystyle \arcsin x}$ en ${\displaystyle [-1,1]}$ como a inversa da restrición de ${\displaystyle \operatorname {sen} \theta }$ ao intervalo ${\displaystyle [-\pi /2,\pi /2]}$: hai infinitos números reais ${\displaystyle \theta }$ con ${\displaystyle \operatorname {sen} \theta =x}$, pero elíxese arbitrariamente o que está en ${\displaystyle [-\pi /2,\pi /2]}$.

Outra maneira de resolver a indeterminación é considerar o logaritmo como unha función cuxo dominio non é unha rexión do plano complexo, senón unha superficie de Riemann que recobre o plano complexo perforado dunha maneira infinita-a-1. As ramas teñen a vantaxe de poderse definir como funcións de variable complexa.. Pola súa banda, a función sobre a superficie de Riemann é elegante porque reúne todas as ramas do logaritmo e non require unha elección arbitraria como parte da súa definición.

Valor principal

Definición

Para cada número complexo non nulo ${\displaystyle z}$, o valor principal ${\displaystyle \operatorname {Log} z}$ é o logaritmo cuxa parte imaxinaria pertence ao intervalo ${\displaystyle (-\pi ,\pi ]}$.^[2] A expresión ${\displaystyle \operatorname {Log} 0}$ queda sen definir, xa que non existe número complexo ${\displaystyle w}$ que cumpra ${\displaystyle e^{w}=0}$.^[1]

Cando aparece a notación ${\displaystyle \log z}$ sen especificar ningún logaritmo en particular, xeralmente interprétase como o valor principal. En particular, isto dá un valor consistente co logaritmo natural ${\displaystyle \ln z}$ cando ${\displaystyle z}$ é un número real positivo. Algúns autores empregan a maiúscula ${\displaystyle {\text{Log}}}$ para distinguir o valor principal doutros logaritmos de ${\displaystyle z}$.^[2]

Cálculo do valor principal

A forma polar dun número complexo non nulo ${\displaystyle z=x+yi}$ é ${\displaystyle z=re^{i\theta }}$, onde ${\displaystyle r=|z|={\sqrt {x^{2}+y^{2}}}}$ é o valor absoluto de ${\displaystyle z}$, e ${\displaystyle \theta }$ é o seu argumento. O valor absoluto é real e positivo. O argumento está definido até unha constante aditiva de múltiplos enteiros de ${\displaystyle 2\pi }$. O seu valor principal é o que pertence ao intervalo ${\displaystyle (-\pi ,\pi ]}$, que se expresa como ${\displaystyle \operatorname {atan2} (y,x)}$.

Isto leva á seguinte fórmula para o valor principal do logaritmo complexo:

${\displaystyle \operatorname {Log} z=\ln r+i\theta =\ln |z|+i\operatorname {Arg} z=\ln {\sqrt {x^{2}+y^{2}}}+i\operatorname {atan2} (y,x).}$

Por exemplo, ${\displaystyle \operatorname {Log} (-3i)=\ln 3-\pi i/2}$, e ${\displaystyle \operatorname {Log} (-3)=\ln 3+\pi i}$.

O valor principal como función inversa

Outra maneira de describir ${\displaystyle \operatorname {Log} z}$ é como a inversa dunha restrición da función exponencial complexa. A faixa horizontal ${\displaystyle S}$ formada polos números complexos ${\displaystyle w=x+yi}$ tales que ${\displaystyle -\pi <y\leq \pi }$ é un exemplo dunha rexión que non contén dous números que difiran nun múltiplo enteiro de ${\displaystyle 2\pi i}$. Polo tanto, a restrición da función exponencial a ${\displaystyle S}$ admite unha función inversa. De feito, a función exponencial aplica ${\displaystyle S}$ bixectivamente sobre o plano complexo perforado ${\displaystyle \mathbb {C} ^{*}=\mathbb {C} \setminus \{0\}}$, e a inversa desta restrición é ${\displaystyle \operatorname {Log} \colon \mathbb {C} ^{*}\to S}$. A sección sobre aplicacións conformes explica con máis detalle as propiedades xeométricas deste mapeo.

O valor principal como continuación analítica

Na rexión ${\displaystyle \mathbb {C} -\mathbb {R} _{\leq 0}}$ formada polos números complexos que non son negativos reais nin cero, a función ${\displaystyle \operatorname {Log} z}$ é a continuación analítica do logaritmo natural. Os valores sobre a recta real negativa poden obterse como límites de valores de puntos complexos veciños cunha parte imaxinaria positiva.

Propiedades

Non todas as identidades que cumpre ${\displaystyle \ln }$ se estenden aos números complexos. É certo que ${\displaystyle e^{\operatorname {Log} z}=z}$ para todo ${\displaystyle z\not =0}$ (iso é o que significa que ${\displaystyle \operatorname {Log} z}$ é un logaritmo de ${\displaystyle z}$), pero a identidade ${\displaystyle \operatorname {Log} (e^{z})=z}$ falla para ${\displaystyle z}$ fóra da faixa ${\displaystyle S}$. Por esta razón, non se pode aplicar ${\displaystyle {\text{Log}}}$ a ambos lados dunha identidade do tipo ${\displaystyle e^{z}=e^{w}}$ para concluír que ${\displaystyle z=w}$. Tamén pode fallar a identidade ${\displaystyle \operatorname {Log} (z_{1}z_{2})=\operatorname {Log} z_{1}+\operatorname {Log} z_{2}}$: os dous lados poden diferir nun múltiplo enteiro de ${\displaystyle 2\pi i}$.^[1] Por exemplo:

${\displaystyle \operatorname {Log} ((-1)i)=\operatorname {Log} (-i)=\ln(1)-{\frac {\pi i}{2}}=-{\frac {\pi i}{2}},}$

pero

${\displaystyle \operatorname {Log} (-1)+\operatorname {Log} (i)=\left(\ln(1)+\pi i\right)+\left(\ln(1)+{\frac {\pi i}{2}}\right)={\frac {3\pi i}{2}}\neq -{\frac {\pi i}{2}}.}$

A función ${\displaystyle \operatorname {Log} z}$ é descontinua en cada número real negativo, pero continua en todo o demais en ${\displaystyle \mathbb {C} ^{*}}$. Para explicar a descontinuidade, considérase o que ocorre co argumento ${\displaystyle \arg z}$ cando ${\displaystyle z}$ se achega a un número real negativo ${\displaystyle a}$. Se ${\displaystyle z}$ se achega a ${\displaystyle a}$ desde arriba, entón ${\displaystyle \arg z}$ tende a ${\displaystyle \pi }$, que é tamén o valor de ${\displaystyle \arg a}$. Pero se ${\displaystyle z}$ se achega desde abaixo, entón ${\displaystyle \arg z}$ tende a ${\displaystyle -\pi }$. Polo tanto, ${\displaystyle \arg z}$ "salta" ${\displaystyle 2\pi }$ ao cruzar o eixe real negativo, e así ${\displaystyle \operatorname {Log} z}$ tamén salta en ${\displaystyle 2\pi i}$.

Ramas do logaritmo complexo

Existe algún xeito alternativo de escoller un logaritmo de cada número complexo non nulo para definir unha función ${\displaystyle \operatorname {L} (z)}$ que sexa continua en todo ${\displaystyle \mathbb {C} ^{*}}$? A resposta é non. Para velo, imaxinemos que seguimos unha función deste tipo ao longo da circunferencia unitaria, avaliando ${\displaystyle \operatorname {L} \left(e^{i\theta }\right)}$ a medida que ${\displaystyle \theta }$ aumenta de ${\displaystyle 0}$ a ${\displaystyle 2\pi }$. Se ${\displaystyle \operatorname {L} (z)}$ é continua, tamén o é ${\displaystyle \operatorname {L} \left(e^{i\theta }\right)-i\theta }$, pero esta última é diferenza de dous logaritmos de ${\displaystyle e^{i\theta }}$, así que toma valores no conxunto discreto ${\displaystyle 2\pi i\mathbb {Z} }$ e, polo tanto, é constante. En particular, ${\displaystyle \operatorname {L} \left(e^{2\pi i}\right)-2\pi i=\operatorname {L} \left(e^{0}\right)-0}$, o que contradí ${\displaystyle \operatorname {L} \left(e^{2\pi i}\right)=\operatorname {L} \left(e^{0}\right)}$.

Para obter un logaritmo continuo definido en números complexos, é necesario restrinxir o dominio a un subconxunto máis pequeno ${\displaystyle U}$ do plano complexo. Como un dos obxectivos é que a función sexa derivable, é razoable supoñer que está definida nun entorno de cada punto do seu dominio, é dicir, que ${\displaystyle U}$ sexa un conxunto aberto. Tamén é razoable asumir que ${\displaystyle U}$ sexa conexo, pois en caso contrario os valores da función nas distintas compoñentes de ${\displaystyle U}$ poderían non estar relacionados. Todo isto motiva a seguinte definición:

Unha rama de ${\displaystyle \log z}$ é unha función continua ${\displaystyle \operatorname {L} (z)}$ definida nun subconxunto aberto conexo ${\displaystyle U}$ do plano complexo tal que ${\displaystyle \operatorname {L} (z)}$ é un logaritmo de ${\displaystyle z}$ para cada ${\displaystyle z}$ en ${\displaystyle U}$.^[2]

Por exemplo, o valor principal define unha rama no conxunto aberto onde é continua, que é ${\displaystyle \mathbb {C} -\mathbb {R} _{\leq 0}}$, obtido eliminando o 0 e os números reais negativos do plano complexo.

Outro exemplo: a serie de Mercator

${\displaystyle \ln(1+u)=\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}u^{n}=u-{\frac {u^{2}}{2}}+{\frac {u^{3}}{3}}-\cdots }$

converxe localmente uniformemente para ${\displaystyle |u|<1}$, así que poñendo ${\displaystyle z=1+u}$ defínese unha rama de ${\displaystyle \log z}$ no disco aberto de raio 1 centrado en 1. (En realidade, esta é só unha restrición de ${\displaystyle \operatorname {Log} z}$, como se pode ver derivando a diferenza e comparando valores en 1.)

Unha vez fixada unha rama, pódese denotar como ${\displaystyle \log z}$ se non hai risco de confusión. Porén, diferentes ramas poden dar valores distintos para o logaritmo dun número complexo, así que hai que fixar previamente a rama (ou entender que se usa o valor principal) para que "${\displaystyle \log z}$" teña un significado preciso e non ambiguo.

Nalgúns textos úsase a notación ${\displaystyle \ln _{k}z}$ para denotar explicitamente a ${\displaystyle k}$-ésima rama do logaritmo complexo. Esta notación é útil cando se traballa con logaritmos multivalorados na análise complexa e na topoloxía. Foi introducida por primeira vez no artigo Unwinding the Branches of the Lambert W function^[5] e foi mencionada posteriormente no traballo de David Jeffrey.^[6]

Cortes de rama

O razoamento anterior sobre a circunferencia unitaria xeralízase para mostrar que non pode existir ningunha rama de ${\displaystyle \log z}$ nun conxunto aberto ${\displaystyle U}$ que conteña unha curva pechada que se enrole arredor do 0. Dise entón que ${\displaystyle \log z}$ ten un punto de rama no 0. Para evitar conter curvas pechadas que se enrolen arredor de 0, ${\displaystyle U}$ adoita escollerse como o complemento dunha semirrecta ou curva no plano complexo que vaia desde 0 (incluído) ata o infinito en certa dirección. Nese caso, a curva chámase un corte de rama. Por exemplo, o valor principal ten un corte de rama ao longo do eixe real negativo.

Se se intenta estender a función ${\displaystyle \operatorname {L} (z)}$ para que estea definida nun punto do corte de rama, entón será necesariamente descontinua nese punto; como moito poderá ser continua “por un lado”, como lle ocorre a ${\displaystyle \operatorname {Log} z}$ nos números reais negativos.

Derivada do logaritmo complexo

Cada rama ${\displaystyle \operatorname {L} (z)}$ de ${\displaystyle \log z}$ nun conxunto aberto ${\displaystyle U}$ é o inverso dunha restrición da función exponencial, concretamente a restrición á imaxe ${\displaystyle \operatorname {L} (U)}$. Como a función exponencial é función holomorfa (é dicir, diferenciábel no sentido complexo) e ten derivada non nula, aplícase o análogo complexo do teorema da función inversa. Isto mostra que ${\displaystyle \operatorname {L} (z)}$ é holomorfa en ${\displaystyle U}$ e que ${\displaystyle \operatorname {L} '(z)=1/z}$ para todo ${\displaystyle z}$ en ${\displaystyle U}$.^[2] Outra maneira de demostrar isto é comprobar as ecuacións de Cauchy–Riemann en coordenadas polares.^[2]

Construción de ramas mediante integración

A función ${\displaystyle \ln(x)}$ para ${\displaystyle x>0}$ real pode construírse mediante a fórmula $${\displaystyle \ln(x)=\int _{1}^{x}{\frac {du}{u}}.}$$ Se o intervalo de integración comeza nun número positivo ${\displaystyle a}$ distinto de 1, a fórmula debe escribirse como $${\displaystyle \ln(x)=\ln(a)+\int _{a}^{x}{\frac {du}{u}}}$$ no seu lugar.

Ao desenvolver o análogo para o logaritmo complexo, xorde unha complicación adicional: a definición da integral complexa require escoller un camiño de integración. Por sorte, se o integrando é holomorfo, entón o valor da integral non cambia ao deformar o camiño (mantendo fixos os extremos), e nun conxunto ${\displaystyle U}$ simplemente conexo (un dominio sen "buracos"), calquera camiño entre ${\displaystyle a}$ e ${\displaystyle z}$ dentro de ${\displaystyle U}$ pode ser continuamente deformado dentro de ${\displaystyle U}$ ata calquera outro. Todo isto leva ao seguinte:

Se ${\displaystyle U}$ é un subconxunto aberto e simplemente conexo de ${\displaystyle \mathbb {C} }$ que non contén o 0, entón pódese construír unha rama de ${\displaystyle \log z}$ definida en ${\displaystyle U}$ escollendo un punto inicial ${\displaystyle a}$ en ${\displaystyle U}$, escollendo un logaritmo ${\displaystyle b}$ de ${\displaystyle a}$, e definindo

$${\displaystyle L(z)=b+\int _{a}^{z}{\frac {dw}{w}}}$$

para cada ${\displaystyle z}$ en ${\displaystyle U}$.^[7]

O logaritmo complexo como aplicación conforme

Os círculos Re(Log z) = constante e os raios Im(Log z) = constante no plano complexo z.

A aplicación logarítmica transforma raios en liñas horizontais e círculos en liñas verticais

Calquera aplicación holomorfa f: U → ℂ tal que f '(z) ≠ 0 para todo z ∈ U é unha aplicación conforme, o que significa que se dúas curvas que pasan por un punto a de U forman un ángulo α (no sentido de que as liñas tanxentes ás curvas en a forman un ángulo α), entón as imaxes das dúas curvas forman o *mesmo* ángulo α no punto f(a).

Como unha rama de log z é holomorfa e a súa derivada 1/z nunca se anula, defínese así unha aplicación conforme.

Por exemplo, a rama principal w = Log z, vista como unha aplicación desde ℂ − ℝ_{≤ 0} cara á banda horizontal definida por |Im z| < π, ten as seguintes propiedades, que son consecuencias directas da súa expresión en coordenadas polares:

• Os círculos^[8] no plano z centrados na orixe son transformados en segmentos verticais no plano w que conectan a − πi con a + πi, onde a é o logaritmo real do raio do círculo.
• Os raios que emanan da orixe no plano z son transformados en liñas horizontais no plano w.

Cada círculo e raio no plano z como os descritos anteriormente intersécanse formando un ángulo recto. As súas imaxes baixo Log son un segmento vertical e unha liña horizontal, respectivamente, no plano w, e tamén se cortan en ángulo recto. Isto ilustra a propiedade conforme de Log.

A superficie de Riemann asociada

Visualización da superficie de Riemann de log z. A superficie parece xirar arredor dunha liña vertical correspondente á orixe do plano complexo. A superficie real esténdese arbitrariamente tanto en horizontal como en vertical, pero está recortada nesta imaxe.

Construción

As diferentes ramas de log z non se poden pegar para formar unha única función continua log: ℂ^* → ℂ, porque dúas ramas poden dar valores distintos nun mesmo punto onde ambas están definidas. Por exemplo, compárense a rama principal Log z definida en ℂ − ℝ_{≤ 0}, cuxa parte imaxinaria θ está en (−π, π), coa rama L(z) definida en ℂ − ℝ_{≥ 0} cuxa parte imaxinaria está en (0, 2π). Ambas coinciden no semiplano superior, pero non no inferior. Polo tanto, ten sentido pegar os dominios desas ramas unicamente polas copias compartidas do semiplano superior. O dominio resultante é conexo, pero ten dúas copias do semiplano inferior. Esas dúas copias pódense visualizar como dous niveis dun aparcadoiro en espiral, e pódese subir desde o nivel da Log ao da L xirando 2π radianes en sentido antihorario arredor de 0, primeiro cruzando o eixe real positivo (no nivel da Log) cara ao semiplano superior compartido, e logo cruzando o eixe real negativo (no nivel da L) ata o nivel inferior da L.

Pódese continuar o proceso pegando ramas cuxa parte imaxinaria θ estea en (π, 3π), en (2π, 4π), e así sucesivamente, ou en dirección oposta con θ en (−2π, 0), (−3π, −π), etc. O resultado final é unha superficie conexa que se pode ver como un aparcadoiro helicoidal con infinitos niveis tanto cara arriba como cara abaixo. Esta é a superficie de Riemann R asociada ao logaritmo complexo.^[9]

Un punto en R pode representarse como un par (z, θ), onde θ é un valor posible do argumento de z. Deste xeito, R pode considerarse embebida en ℂ × ℝ ≃ ℝ³.

A función logarítmica na superficie de Riemann

Como os dominios das ramas se pegaron unicamente nos abertos onde os seus valores coincidían, as ramas forman unha única función ben definida log_R: R → ℂ.^[10] Esta envía cada punto (z, θ) en R a ln|z| + iθ. Este proceso de estender a rama principal mediante o pegado de funcións holomorfas compatibles coñécese como prolongación analítica.

Hai unha “aplicación de proxección” desde R cara a ℂ^* que “aplana” a espiral, enviando (z, θ) a z. Para calquera z en ℂ^*, se se toman todos os puntos (z, θ) de R que están “directamente enriba” de z e se avalía log_R en todos eles, obtense o conxunto de todos os logaritmos de z.

Pegando todas as ramas de log z

En lugar de pegar só as ramas escollidas anteriormente, pódese comezar con *todas* as ramas de log z e pegar simultaneamente *cada par* de ramas L₁: U₁ → ℂ e L₂: U₂ → ℂ no maior aberto do intersección U₁ ∩ U₂ onde coincidan. Isto produce a mesma superficie de Riemann R e a mesma función log_R que antes. Este enfoque, aínda que máis difícil de visualizar, é máis natural porque non require escoller ningunha rama concreta.

Se U′ é un subconxunto aberto de R que se proxecta bixectivamente sobre a súa imaxe U en ℂ^*, entón a restrición de log_R a U′ corresponde a unha rama de log z definida en U. Todas as ramas de log z xorden deste xeito.

A superficie de Riemann como recubrimento universal

A aplicación de proxección R → ℂ^* realiza R como un espazo de recubrimento de ℂ^*. De feito, trátase dun recubrimento de Galois cun grupo de automorfismos de cuberta isomorfo a ℤ, xerado polo homeomorfismo que envía (z, θ) a (z, θ + 2π).

Como variedade complexa, R é biholomorfa con ℂ a través da función log_R. (A aplicación inversa envía z a (e^z, Im(z)).) Isto mostra que R é simplemente conexa, polo que é o recubrimento universal de ℂ^*.

Aplicacións

• O logaritmo complexo é necesario para definir a exponenciación cando a base é un número complexo. En efecto, se ${\displaystyle a}$ e ${\displaystyle b}$ son números complexos con ${\displaystyle a\not =0}$, pódese usar o valor principal para definir ${\displaystyle a^{b}=e^{b\operatorname {Log} a}}$. Tamén se pode substituír ${\displaystyle \operatorname {Log} a}$ por outros logaritmos de ${\displaystyle a}$ para obter outros valores de ${\displaystyle a^{b}}$, que difiren por factores da forma ${\displaystyle e^{2\pi inb}}$.^[1][11] A expresión ${\displaystyle a^{b}}$ ten un único valor se e só se ${\displaystyle b}$ é un número enteiro.^[1]
• Como as funcións trigonométricas poden expresarse como funcións racionais de ${\displaystyle e^{iz}}$, as funcións trigonométricas inversas poden expresarse en termos de logaritmos complexos.
• En enxeñaría eléctrica, a constante de propagación implica un logaritmo complexo.

Xeneralizacións

Logaritmos con outras bases

Do mesmo xeito que cos números reais, pódese definir para números complexos ${\displaystyle b}$ e ${\displaystyle x}$:

${\displaystyle \log _{b}x={\frac {\log x}{\log b}},}$

co único matiz de que o seu valor depende da elección dunha rama do logaritmo definida en ${\displaystyle b}$ e ${\displaystyle x}$ (e con ${\displaystyle \log b\not =0}$). Por exemplo, usando o valor principal obtense:

${\displaystyle \log _{i}e={\frac {\operatorname {Log} e}{\operatorname {Log} i}}={\frac {1}{\pi i/2}}=-{\frac {2i}{\pi }}.}$

Logaritmos de funcións holomorfas

Se ${\displaystyle f}$ é unha función holomorfa nun subconxunto aberto e conexo ${\displaystyle U}$ de ${\displaystyle \mathbb {C} }$, entón unha rama de ${\displaystyle \log f}$ en ${\displaystyle U}$ é unha función continua ${\displaystyle g}$ sobre ${\displaystyle U}$ tal que ${\displaystyle e^{g(z)}=f(z)}$ para todo ${\displaystyle z}$ en ${\displaystyle U}$. Dita función ${\displaystyle g}$ é necesariamente holomorfa e cumpre ${\displaystyle g'(z)=f'(z)/f(z)}$ para todo ${\displaystyle z}$ en ${\displaystyle U}$.

Se ${\displaystyle U}$ é un subconxunto aberto e simplemente conexo de ${\displaystyle \mathbb {C} }$, e ${\displaystyle f}$ é unha función holomorfa en ${\displaystyle U}$ que non se anula en ningún punto, entón pode construírse unha rama de ${\displaystyle \log f}$ en ${\displaystyle U}$ escollendo un punto inicial ${\displaystyle a}$ en ${\displaystyle U}$, escollendo un logaritmo ${\displaystyle b}$ de ${\displaystyle f(a)}$, e definindo

${\displaystyle g(z)=b+\int _{a}^{z}{\frac {f'(w)}{f(w)}}\,dw}$

para cada ${\displaystyle z}$ en ${\displaystyle U}$.^[2]