Produto de matrices

En matemáticas, particularmente en álxebra lineal, a multiplicación de matrices é unha operación binaria que produce unha matriz a partir de dúas matrices. Para a multiplicación de matrices, o número de columnas da primeira matriz debe ser igual ao número de filas da segunda matriz. A matriz resultante, coñecida como produto matricial, ten o número de filas da primeira e o número de columnas da segunda matriz. O produto das matrices A e B denotase como AB.^[1]

Para a multiplicación de matrices, o número de columnas da primeira matriz debe ser igual ao número de filas da segunda matriz. A matriz de resultados ten o número de filas da primeira e o número de columnas da segunda.

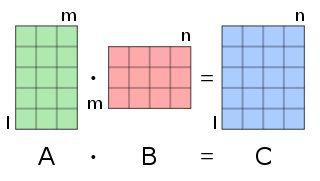
O cálculo de produtos matriciales é unha operación central en todas as aplicacións computacionais da álxebra lineal.

Definicións

Produto de matrices

Se A é unha matriz m × n e B é unha matriz n × p, $${\displaystyle \mathbf {A} ={\begin{pmatrix}a_{11}&a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}&\cdots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{m1}&a_{m2}&\cdots &a_{mn}\\\end{pmatrix}},\quad \mathbf {B} ={\begin{pmatrix}b_{11}&b_{12}&\cdots &b_{1p}\\b_{21}&b_{22}&\cdots &b_{2p}\\\vdots &\vdots &\ddots &\vdots \\b_{n1}&b_{n2}&\cdots &b_{np}\\\end{pmatrix}}}$$ o produto matricial C = AB (indicado sen signos ou puntos de multiplicación) defínese como a matriz m × p^[2][3][4][5]

${\displaystyle \mathbf {C} ={\begin{pmatrix}c_{11}&c_{12}&\cdots &c_{1p}\\c_{21}&c_{22}&\cdots &c_{2p}\\\vdots &\vdots &\ddots &\vdots \\c_{m1}&c_{m2}&\cdots &c_{mp}\\\end{pmatrix}}}$ tal que

${\displaystyle c_{ij}=a_{i1}b_{1j}+a_{i2}b_{2j}+\cdots +a_{in}b_{nj}=\sum _{k=1}^{n}a_{ik}b_{kj},}$ para i = 1, ..., m; i = 1, ..., m e j = 1, ..., p j = 1, ..., p.

É dicir, o elemento c_{ij} do produto obtense multiplicando termo por termo as entradas da i-ésima fila de A e a j-ésima columna de B, e sumando estes n produtos. Noutras palabras, c_{ij} é o produto escalar da i-ésima fila de A e a j-ésima columna de B.

Por tanto, o produto AB defínese se e só se o número de columnas en A é igual ao número de filas en B,^[1] neste caso n.

A figura seguinte mostra como calcular os coeficientes ${\displaystyle c_{12}}$ e ${\displaystyle c_{33}}$ da matriz produto ${\displaystyle AB}$ se ${\displaystyle A}$ é unha matriz de tipo ${\displaystyle (4,2)}$, et ${\displaystyle B}$ é unha matriz de tipo ${\displaystyle (2,3)}$.

${\displaystyle {\color {BrickRed}c_{12}}=\sum _{r=1}^{2}a_{1r}b_{r2}=a_{11}b_{12}+a_{12}b_{22}}$

${\displaystyle {\color {NavyBlue}c_{33}}=\sum _{r=1}^{2}a_{3r}b_{r3}=a_{31}b_{13}+a_{32}b_{23}}$

Exemplos

${\displaystyle {\begin{pmatrix}1&0\\2&-1\end{pmatrix}}\times {\begin{pmatrix}3&4\\-2&-3\\\end{pmatrix}}}$

${\displaystyle ={\begin{pmatrix}(1\times 3+0\times -2)&(1\times 4+0\times -3)\\(2\times 3+-1\times -2)&(2\times 4+-1\times -3)\end{pmatrix}}={\begin{pmatrix}3&4\\8&11\end{pmatrix}}}$.

En xeral, o produto des matrices non é conmutativa, Isto é, ${\displaystyle AB}$ non é igual a ${\displaystyle BA}$, como mostra o seguinte exemplo:

${\displaystyle {\begin{pmatrix}1&2&0\\4&3&-1\\\end{pmatrix}}\times {\begin{pmatrix}5&1\\2&3\\3&4\\\end{pmatrix}}={\begin{pmatrix}9&7\\23&9\\\end{pmatrix}}}$,

mentres que,

${\displaystyle {\begin{pmatrix}5&1\\2&3\\3&4\\\end{pmatrix}}\times {\begin{pmatrix}1&2&0\\4&3&-1\\\end{pmatrix}}={\begin{pmatrix}9&13&-1\\14&13&-3\\19&18&-4\\\end{pmatrix}}}$

Produto escalar

O produto escalar ${\displaystyle \mathbf {a} \cdot \mathbf {b} }$ de dous vectores ${\displaystyle \mathbf {a} }$ e ${\displaystyle \mathbf {b} }$ de igual lonxitude é igual a un elemento único (sería unha matriz ${\displaystyle 1\times 1}$) resultante de multiplicar estes vectores como un vector fila por un vector columna, así: ${\displaystyle \mathbf {a} ^{\mathrm {T} }\mathbf {b} }$ (ou ${\displaystyle \mathbf {b} ^{\mathrm {T} }\mathbf {a} }$).

O produto escalar dos dous vectores

${\displaystyle a={\begin{pmatrix}1\\2\\3\end{pmatrix}}}$  e  ${\displaystyle b={\begin{pmatrix}-7\\8\\9\end{pmatrix}}}$

calcúlase como

${\displaystyle a\cdot b={\begin{pmatrix}1&2&3\end{pmatrix}}{\begin{pmatrix}-7\\8\\9\end{pmatrix}}=1\cdot (-7)+2\cdot 8+3\cdot 9=36}$.

Potencia dunha matriz cadrada

A potencia dunha matriz sería unha multiplicación repetida, o que pode realizarse cando a matriz é cadrada.

Cando unha matriz ${\displaystyle A}$ cadrada é diagonalizábel esta diagonalización ${\displaystyle A=PDP^{-1}}$, onde ${\displaystyle D}$ é unha matriz diagonal, pódese usar para calcular eficientemente as potencias dunha matriz:

${\displaystyle {\begin{aligned}A^{k}&=\left(PDP^{-1}\right)^{k}=\left(PDP^{-1}\right)\left(PDP^{-1}\right)\cdots \left(PDP^{-1}\right)\\&=PD\left(P^{-1}P\right)D\left(P^{-1}P\right)\cdots \left(P^{-1}P\right)DP^{-1}=PD^{k}P^{-1},\end{aligned}}}$

e isto último é doado de calcular xa que só implica as potencias dunha matriz diagonal. Por exemplo, para a matriz ${\displaystyle A}$

${\displaystyle A=\left[{\begin{array}{rrr}0&1&\!\!\!-2\\0&1&0\\1&\!\!\!-1&3\end{array}}\right].}$

con valores propios ${\displaystyle \lambda =1,1,2}$ temos a diagonalización: ${\displaystyle P}$ to get: $${\displaystyle P^{-1}AP=\left[{\begin{array}{rrr}1&0&1\\1&2&0\\0&1&\!\!\!\!-1\end{array}}\right]^{-1}\left[{\begin{array}{rrr}0&1&\!\!\!-2\\0&1&0\\1&\!\!\!-1&3\end{array}}\right]\left[{\begin{array}{rrr}1&\,0&1\\1&2&0\\0&1&\!\!\!\!-1\end{array}}\right]={\begin{bmatrix}1&0&0\\0&1&0\\0&0&2\end{bmatrix}}=D.}$$ e agora calculamos:

${\displaystyle {\begin{aligned}A^{k}=PD^{k}P^{-1}&=\left[{\begin{array}{rrr}1&\,0&1\\1&2&0\\0&1&\!\!\!\!-1\end{array}}\right]{\begin{bmatrix}1^{k}&0&0\\0&1^{k}&0\\0&0&2^{k}\end{bmatrix}}\left[{\begin{array}{rrr}1&\,0&1\\1&2&0\\0&1&\!\!\!\!-1\end{array}}\right]^{-1}\\[1em]&={\begin{bmatrix}2-2^{k}&-1+2^{k}&2-2^{k+1}\\0&1&0\\-1+2^{k}&1-2^{k}&-1+2^{k+1}\end{bmatrix}}.\end{aligned}}}$

Aplicacións fundamentais

Historicamente, a multiplicación matricial foi introducida para facilitar e aclarar os cálculos en álxebra linear.

Mapas lineares

Un mapa linear A dun espazo vectorial de dimensión n nun espazo vectorial de dimensión m mapea un vector columna

${\displaystyle \mathbf {x} ={\begin{pmatrix}x_{1}\\x_{2}\\\vdots \\x_{n}\end{pmatrix}}}$

sobre o vector columna

${\displaystyle \mathbf {y} =A(\mathbf {x} )={\begin{pmatrix}a_{11}x_{1}+\cdots +a_{1n}x_{n}\\a_{21}x_{1}+\cdots +a_{2n}x_{n}\\\vdots \\a_{m1}x_{1}+\cdots +a_{mn}x_{n}\end{pmatrix}}.}$

O mapa linear A está así definido pola matriz

${\displaystyle \mathbf {A} ={\begin{pmatrix}a_{11}&a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}&\cdots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{m1}&a_{m2}&\cdots &a_{mn}\\\end{pmatrix}},}$

e mapea o vector columna ${\displaystyle \mathbf {x} }$ no produto matricial

${\displaystyle \mathbf {y} =\mathbf {Ax} .}$

Rotacións xeométricas

Usando un sistema de coordenadas cartesianas nun plano euclidiano, a rotación dun ángulo ${\displaystyle \alpha }$ arredor da orixe é un mapa linear. Máis precisamente,

${\displaystyle {\begin{bmatrix}x'\\y'\end{bmatrix}}={\begin{bmatrix}\cos \alpha &-\sin \alpha \\\sin \alpha &\cos \alpha \end{bmatrix}}{\begin{bmatrix}x\\y\end{bmatrix}},}$

onde o punto de orixe ${\displaystyle (x,y)}$ e a súa imaxe ${\displaystyle (x',y')}$ escríbense como vectores columna.

Sistema de ecuacións lineares

A forma xeral dun sistema de ecuacións lineares é

${\displaystyle {\begin{matrix}a_{11}x_{1}+\cdots +a_{1n}x_{n}=b_{1},\\a_{21}x_{1}+\cdots +a_{2n}x_{n}=b_{2},\\\vdots \\a_{m1}x_{1}+\cdots +a_{mn}x_{n}=b_{m}.\end{matrix}}}$

Usando a mesma notación anterior, tal sistema é equivalente á ecuación matricial única

${\displaystyle \mathbf {Ax} =\mathbf {b} .}$

Produto escalar, forma bilinear e forma sesquilinear

O produto escalar de dous vectores columna é o único elemento do produto matricial

${\displaystyle \mathbf {x} ^{\mathsf {T}}\mathbf {y} ,}$

onde ${\displaystyle \mathbf {x} ^{\mathsf {T}}}$ é o vector fila obtido mediante a transposición de ${\displaystyle \mathbf {x} }$.

Máis xeralmente, calquera forma bilinear sobre un espazo vectorial de dimensión finita pode expresarse como un produto matricial

${\displaystyle \mathbf {x} ^{\mathsf {T}}\mathbf {Ay} ,}$

e calquera forma sesquilinear pode expresarse como

${\displaystyle \mathbf {x} ^{\dagger }\mathbf {Ay} ,}$

onde ${\displaystyle \mathbf {x} ^{\dagger }}$ denota a transposta conxugada de ${\displaystyle \mathbf {x} }$ (conxugada da transposta, ou equivalentemente transposta da conxugada).

Multiplicación matricial por bloque

Se consideramos as matrices ${\displaystyle M=\left({\begin{smallmatrix}A&B\\C&D\end{smallmatrix}}\right)}$ e ${\displaystyle N=\left({\begin{smallmatrix}A'&B'\\C'&D'\end{smallmatrix}}\right)}$, onde ${\displaystyle A,A',B,B',C,C'}$ e ${\displaystyle D,D'}$ son matrices que verifican:

• O número de columnas en ${\displaystyle A}$ e ${\displaystyle C}$ é igual ao número de filas en ${\displaystyle A'}$ e ${\displaystyle B'}$
• O número de columnas en ${\displaystyle B}$ e ${\displaystyle D}$ é igual ao número de filas en ${\displaystyle C'}$ e ${\displaystyle D'}$

entón temos a igualdade

${\displaystyle MN={\begin{pmatrix}AA'+BC'&AB'+BD'\\CA'+DC'&CB'+DD'\end{pmatrix}}}$

Observe a analoxía entre o produto da matriz de bloques e o produto de dúas matrices cadradas de orde 2. por tanto isto non define unha nova forma de produto de matrices. Este é simplemente un método de cálculo de produto matricial común que pode simplificar os cálculos.

Produto de Hadamard

Artigo principal: Produto de Hadamard.

Para dúas matrices do mesmo tipo, temos o "produto Hadamard" ou produto compoñente por compoñente. O produto de Hadamard de dúas matrices ${\displaystyle A=(a_{ij})}$ e ${\displaystyle B=(b_{ij})}$ de tipo ${\displaystyle (m,n)}$, denotado A · B = (c_ij) , é unha matriz de tipo ${\displaystyle (m,n)}$ dada por

${\displaystyle c_{ij}=a_{ij}\times b_{ij}.}$

Por exemplo:

${\displaystyle {\begin{pmatrix}1&3&2\\1&0&0\\1&2&2\end{pmatrix}}\cdot {\begin{pmatrix}0&0&2\\7&5&0\\2&1&1\end{pmatrix}}={\begin{pmatrix}1\times 0&3\times 0&2\times 2\\1\times 7&0\times 5&0\times 0\\1\times 2&2\times 1&2\times 1\end{pmatrix}}={\begin{pmatrix}0&0&4\\7&0&0\\2&2&2\end{pmatrix}}.}$

Este produto é unha submatriz do produto de Kronecker.

Produto de Kronecker

Artigo principal: Produto de Kronecker.

Para dúas matrices arbitrarias ${\displaystyle A=(a_{ij})}$ e ${\displaystyle B}$, temos o produto tensor ou produto de Kronecker A ⊗ B que se define por

${\displaystyle {\begin{pmatrix}a_{11}B&a_{12}B&\cdots &a_{1n}B\\\vdots &\vdots &\ddots &\vdots \\a_{m1}B&a_{m2}B&\cdots &a_{mn}B\end{pmatrix}}}$

Se ${\displaystyle A}$ é unha matriz de tipo ${\displaystyle (m,n)}$ e ${\displaystyle B}$ é unha matriz de tipo ${\displaystyle (p,r)}$ daquela A ⊗ B é unha matriz de tipo ${\displaystyle (mp,nr)}$. De novo esta multiplicación non é conmutativa.

Por exemplo

${\displaystyle {\begin{pmatrix}1&2\\3&1\\\end{pmatrix}}\otimes {\begin{pmatrix}0&3\\2&1\\\end{pmatrix}}={\begin{pmatrix}1\times 0&1\times 3&2\times 0&2\times 3\\1\times 2&1\times 1&2\times 2&2\times 1\\3\times 0&3\times 3&1\times 0&1\times 3\\3\times 2&3\times 1&1\times 2&1\times 1\\\end{pmatrix}}={\begin{pmatrix}0&3&0&6\\2&1&4&2\\0&9&0&3\\6&3&2&1\end{pmatrix}}}$.

Se ${\displaystyle A}$ e ${\displaystyle B}$ son as matrices de mapas lineares V₁ → W ₁ e V₂ → W₂, respectivamente, logo A ⊗ B representa o produto tensorial dos dous mapas, V₁ ⊗ V₂ → W₁ ⊗ W₂.

Propiedades comúns

Os tres produtos de matrices anteriores, e tamén o produto común de matrices, son asociativos

${\displaystyle A\times (B\times C)=(A\times B)\times C}$,

distributivos en relación coa suma:

${\displaystyle A\times (B+C)=A\times B+A\times C}$

${\displaystyle (A+B)\times C=A\times C+B\times C}$

e compatíbeis coa multiplicación por un escalar:

${\displaystyle c(A\times B)=(cA)\times B=A\times (cB)}$

Multiplicación por un escalar

O produto por un escalar ${\displaystyle r}$ dunha matriz ${\displaystyle A=(a_{ij})}$ dá o resultado

${\displaystyle rA=(ra_{ij})}$.

Se estamos a traballar con matrices nun anel, a multiplicación por un escalar ás veces chámase "multiplicación á esquerda" mentres que "multiplicación á dereita" defínese por:

${\displaystyle Ar=(a_{ij}r)}$.

Cando o anel é un anel conmutativo, por exemplo, o corpo dos reais ou dos complexos, as dúas multiplicacións son idénticas.

Porén, se o anel non é conmutativo, como o dos quaternións, entón poden ser diferentes. Por exemplo

${\displaystyle i{\begin{pmatrix}i&0\\0&j\\\end{pmatrix}}={\begin{pmatrix}-1&0\\0&k\\\end{pmatrix}}\neq {\begin{pmatrix}-1&0\\0&-k\\\end{pmatrix}}={\begin{pmatrix}i&0\\0&j\\\end{pmatrix}}i}$

Outros tipos de produto de matrices

Outros tipos de produtos de matrices, a maiores dos xa vistos, inclúen:

• Produto cracoviano, definido como A ∧ B = B^TA
• Produto interno de Frobenius, o produto escalar das matrices consideradas vectores ou, equivalentemente, a suma das entradas do produto de Hadamard
• Produto Khatri-Rao e produto Face-splitting
• Produto exterior, tamén chamado produto diádico ou produto tensor de matrices de dúas columnas, que é ${\displaystyle \mathbf {a} \mathbf {b} ^{\mathsf {T}}}$