Хиперболични функции

Хиперболични функции – во математиката функции аналогни на тригонометриските, или циркуларните функции.

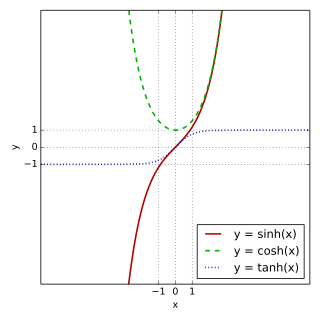
Основни хиперболични функции се:

• хиперболичен синус "sinh"
• хиперболичен косинус "cosh"

од кои се изведени:

• хиперболичен тангенс "tanh"
• хиперболичен косеканс "csch" or "cosech"
• хиперболичен секанс "sech"
• хиперболичен котангенс "coth"

кои соодветствуваат на изведените тригонометриски функции.

Инверзни хиперболични функции се:

• аркус хиперболичен синус "arcsinh" (исто така се бележи како "sinh⁻¹", "asinh" или "arsinh")^[1][2][3]
• и така следователно.

Зрак низ единична хипербола x² − y² = 1 во точката (cosh a, sinh a), каде a е двојна од површината меѓу зракот, хиперболата и x-оската. За точки на хиперболата под x-оската, површината се смета негативна (види анимираната верзија со споредба со тригонометриските (циркуларните) функции).

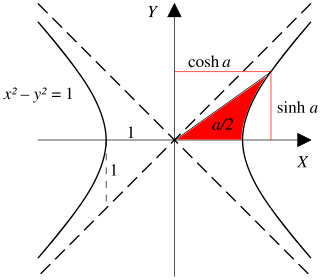
Токму како што точките (cos t, sin t) образуваат круг со единичен радиоу, точките (cosh t, sinh t) ја образуваат десната половина од еднаквостранична хипербола. Хиперболичните функции земаат реален аргумент наречен хиперболичен агол. Големината на хиперболичниот агол е двојна од површината на неговиот хиперболичен сектор. Хиперболичните функции може да се дефинираат врз основа на хиперболичниот триаголник кој го опфаќа овој сектор.

Хиперболични функции постојат во решенијата на многу линеарни диференцијални равенки (на пример, равенката која дефинира верижница), од некои кубни функции, во пресметките на агли и растојанија во хиперболичната геометрија, во Лапласовата равенка во Декартов координатен систем. Лапласовите равенки се битни во многу подрачја на физиката, како електромагнетната теорија, преносот на топлина, динамиката на флуиди и специјалната теорија за релативности.

Во комплексната анализа, хиперболичните функции се јавуваат како имагинарни делови на синус и косинус. Хиперболичниот синус и хиперболичниот косинус се цели функции. Како резултат, другите хиперболични функции се мероморфни во целата комплексна рамнина.

Според Линдеман-Вајерштрасовата теорема, хиперболичните функции имаат трансцендентна вредност за секоја ненулова алгебарска вредност на аргументот.^[4]

Хиперболичните функции биле воведени во 1760-тите, независно од Винченцо Рикати и Јохан Хајнрих Ламберт.^[5] Рикати ги користел Sc. и Cc. (sinus/cosinus circulare) за обележување на циркуларните функции и Sh. и Ch. (sinus/cosinus hyperbolico) за обележување на хиперболичните функции. Ламберт ги прифатил имињата, но ги променил кратенките како што се денес.^[6] Кратенките sh, ch, th, cth исто така се во оптек, нивното користење повеќе зависи од личните претпочитувања на влијателните математичари отколку од јазикот.

Дефиниции

sinh, cosh and tanh

csch, sech and coth

Постојат различни еквиваленти начини за дефинирање на хиперболичните функции.

Дефиниции преку експоненцијална функција

sinh x е половина од разликата од e^x и e^−x

cosh x е аритметичка средина од e^x и e^−x

Хиперболичните функции може да бидат изразени преку експоненцијалната функција:

• Хиперболичен синус: непарниот дел од експоненцијалната функција, кој е

  ${\displaystyle \sinh x={\frac {e^{x}-e^{-x}}{2}}={\frac {e^{2x}-1}{2e^{x}}}={\frac {1-e^{-2x}}{2e^{-x}}}.}$

• Хиперболичен косинус: парниот дел од експоненцијалната функција, кој е

  ${\displaystyle \cosh x={\frac {e^{x}+e^{-x}}{2}}={\frac {e^{2x}+1}{2e^{x}}}={\frac {1+e^{-2x}}{2e^{-x}}}.}$

• Хиперболичен тангенс:

  ${\displaystyle \tanh x={\frac {\sinh x}{\cosh x}}={\frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}={\frac {e^{2x}-1}{e^{2x}+1}}}$

• Хиперболичен котангенс: for x ≠ 0,

  ${\displaystyle \coth x={\frac {\cosh x}{\sinh x}}={\frac {e^{x}+e^{-x}}{e^{x}-e^{-x}}}={\frac {e^{2x}+1}{e^{2x}-1}}}$

• Хиперболичен секанс:

  ${\displaystyle \operatorname {sech} x={\frac {1}{\cosh x}}={\frac {2}{e^{x}+e^{-x}}}={\frac {2e^{x}}{e^{2x}+1}}}$

• Хиперболичен косеканс: for x ≠ 0,

  ${\displaystyle \operatorname {csch} x={\frac {1}{\sinh x}}={\frac {2}{e^{x}-e^{-x}}}={\frac {2e^{x}}{e^{2x}-1}}}$

Дефиниции преку изводи

Хиперболичните функции може да бидат дефинирани како решенија на диференцијални равенки: Хиперболичниот синус и хиперболичниот косинус се единствени решенија (s, c) на системот

${\displaystyle {\begin{aligned}c'(x)&=s(x)\\s'(x)&=c(x)\end{aligned}}}$

како s(0) = 0 and c(0) = 1.

Исто така тие се единствено решение на равенката f ″(x) = f (x), како f (0) = 1, f ′(0) = 0 за хиперболичниот косинус и f (0) = 0, f ′(0) = 1 за хиперболичниот синус.

Тригонометриски дефиниции

Хиперболичните функции исто така може да бидат изведени од тригонометриски функции со комплексни аргументи:

• Хиперболичен синус:

  ${\displaystyle \sinh x=-i\sin(ix)}$

• Хиперболичен косинус:

  ${\displaystyle \cosh x=\cos(ix)}$

• Хиперболичен косинус:

  ${\displaystyle \tanh x=-i\tan(ix)}$

• Хиперболичен котангенс:

  ${\displaystyle \coth x=i\cot(ix)}$

• Хиперболичен секанс:

  ${\displaystyle \operatorname {sech} x=\sec(ix)}$

• Хиперболичен косеканс:

  ${\displaystyle \operatorname {csch} x=i\csc(ix)}$

каде i е имагинарна единица со својство дека i² = −1.

Комплексните облици во дефинициите се изведуваат од Ојлеровата формула.

Својства

Хиперболичен косинус

Може да се покаже дека површината под кривата на хиперболичниот косинус на конечен интервал секогаш е еднаква на должината на соодветниот лак на тој интервал: ^[7]

${\displaystyle {\text{area}}=\int _{a}^{b}\cosh x\,dx=\int _{a}^{b}{\sqrt {1+\left({\frac {d}{dx}}\cosh x\right)^{2}}}\,dx={\text{arc length.}}}$

Хиперболичен тангенс

Хиперболичниот тангенс е решение на диференцијалната равенка f ′ = 1 − f ² со f (0) = 0 и нелинеарниот проблем на гранична вредност:^[8][9]

${\displaystyle {\tfrac {1}{2}}f''=f^{3}-f;\quad f(0)=f'(\infty )=0.}$

Корисни врски

Парни и непарни функции:

${\displaystyle {\begin{aligned}\sinh(-x)&=-\sinh x\\\cosh(-x)&=\cosh x\end{aligned}}}$

Оттука:

${\displaystyle {\begin{aligned}\tanh(-x)&=-\tanh x\\\coth(-x)&=-\coth x\\\operatorname {sech} (-x)&=\operatorname {sech} x\\\operatorname {csch} (-x)&=-\operatorname {csch} x\end{aligned}}}$

Може да се види дека cosh x и sech x се парни; другите се непарни функции.

${\displaystyle {\begin{aligned}\operatorname {arsech} x&=\operatorname {arcosh} \left({\frac {1}{x}}\right)\\\operatorname {arcsch} x&=\operatorname {arsinh} \left({\frac {1}{x}}\right)\\\operatorname {arcoth} x&=\operatorname {artanh} \left({\frac {1}{x}}\right)\end{aligned}}}$

Хиперболичните синус и косинус ги задоволуваат:

${\displaystyle {\begin{aligned}\cosh x+\sinh x&=e^{x}\\\cosh x-\sinh x&=e^{-x}\\\cosh ^{2}x-\sinh ^{2}x&=1\end{aligned}}}$

последниот од нив е сличен на Питагоровиот тригонометриски идентитет.

Исто така

${\displaystyle {\begin{aligned}\operatorname {sech} ^{2}x&=1-\tanh ^{2}x\\\operatorname {csch} ^{2}x&=\coth ^{2}x-1\end{aligned}}}$

за другите функции.

Збир од аргументи

${\displaystyle {\begin{aligned}\sinh(x+y)&=\sinh x\cosh y+\cosh x\sinh y\\\cosh(x+y)&=\cosh x\cosh y+\sinh x\sinh y\\[6px]\tanh(x+y)&={\frac {\tanh x+\tanh y}{1+\tanh x\tanh y}}\\\end{aligned}}}$

особено

${\displaystyle {\begin{aligned}\cosh(2x)&=\sinh ^{2}{x}+\cosh ^{2}{x}=2\sinh ^{2}x+1=2\cosh ^{2}x-1\\\sinh(2x)&=2\sinh x\cosh x\\\tanh(2x)&={\frac {2\tanh x}{1+\tanh ^{2}x}}\\\end{aligned}}}$

Исто така:

${\displaystyle {\begin{aligned}\sinh x+\sinh y&=2\sinh \left({\frac {x+y}{2}}\right)\cosh \left({\frac {x-y}{2}}\right)\\\cosh x+\cosh y&=2\cosh \left({\frac {x+y}{2}}\right)\cosh \left({\frac {x-y}{2}}\right)\\\end{aligned}}}$

Формули за разлика

${\displaystyle {\begin{aligned}\sinh(x-y)&=\sinh x\cosh y-\cosh x\sinh y\\\cosh(x-y)&=\cosh x\cosh y-\sinh x\sinh y\\\tanh(x-y)&={\frac {\tanh x-\tanh y}{1-\tanh x\tanh y}}\\\end{aligned}}}$

Исто така:^[10]

${\displaystyle {\begin{aligned}\sinh x-\sinh y&=2\cosh \left({\frac {x+y}{2}}\right)\sinh \left({\frac {x-y}{2}}\right)\\\cosh x-\cosh y&=2\sinh \left({\frac {x+y}{2}}\right)\sinh \left({\frac {x-y}{2}}\right)\\\end{aligned}}}$

Формули на половина аргумент

${\displaystyle {\begin{aligned}\sinh \left({\frac {x}{2}}\right)&={\frac {\sinh(x)}{\sqrt {2(\cosh x+1)}}}&&=\operatorname {sgn} x\,{\sqrt {\frac {\cosh x-1}{2}}}\\[6px]\cosh \left({\frac {x}{2}}\right)&={\sqrt {\frac {\cosh x+1}{2}}}\\[6px]\tanh \left({\frac {x}{2}}\right)&={\frac {\sinh x}{\cosh x+1}}&&=\operatorname {sgn} x\,{\sqrt {\frac {\cosh x-1}{\cosh x+1}}}={\frac {e^{x}-1}{e^{x}+1}}\end{aligned}}}$

каде sgn е функција сигнум.

Ако x ≠ 0, тогаш^[11]

${\displaystyle \tanh \left({\frac {x}{2}}\right)={\frac {\cosh x-1}{\sinh x}}=\coth x-\operatorname {csch} x}$

Инверзни функции како логаритми

Главна статија: Инверзни хиперболични функции

${\displaystyle {\begin{aligned}\operatorname {arsinh} (x)&=\ln \left(x+{\sqrt {x^{2}+1}}\right)\\\operatorname {arcosh} (x)&=\ln \left(x+{\sqrt {x^{2}-1}}\right)&&x\geqslant 1\\\operatorname {artanh} (x)&={\frac {1}{2}}\ln \left({\frac {1+x}{1-x}}\right)&&|x|<1\\\operatorname {arcoth} (x)&={\frac {1}{2}}\ln \left({\frac {x+1}{x-1}}\right)&&|x|>1\\\operatorname {arsech} (x)&=\ln \left({\frac {1}{x}}+{\sqrt {{\frac {1}{x^{2}}}-1}}\right)=\ln \left({\frac {1+{\sqrt {1-x^{2}}}}{x}}\right)&&0<x\leqslant 1\\\operatorname {arcsch} (x)&=\ln \left({\frac {1}{x}}+{\sqrt {{\frac {1}{x^{2}}}+1}}\right)&&x\neq 0\end{aligned}}}$

Изводи

${\displaystyle {\begin{aligned}{\frac {d}{dx}}\sinh x&=\cosh x\\{\frac {d}{dx}}\cosh x&=\sinh x\\{\frac {d}{dx}}\tanh x&=1-\tanh ^{2}x=\operatorname {sech} ^{2}x={\frac {1}{\cosh ^{2}x}}\\{\frac {d}{dx}}\coth x&=1-\coth ^{2}x=-\operatorname {csch} ^{2}x=-{\frac {1}{\sinh ^{2}x}}&&x\neq 0\\{\frac {d}{dx}}\operatorname {sech} x&=-\tanh x\operatorname {sech} x\\{\frac {d}{dx}}\operatorname {csch} x&=-\coth x\operatorname {csch} x&&x\neq 0\\{\frac {d}{dx}}\operatorname {arsinh} x&={\frac {1}{\sqrt {x^{2}+1}}}\\{\frac {d}{dx}}\operatorname {arcosh} x&={\frac {1}{\sqrt {x^{2}-1}}}&&1<x\\{\frac {d}{dx}}\operatorname {artanh} x&={\frac {1}{1-x^{2}}}&&|x|<1\\{\frac {d}{dx}}\operatorname {arcoth} x&={\frac {1}{1-x^{2}}}&&1<|x|\\{\frac {d}{dx}}\operatorname {arsech} x&=-{\frac {1}{x{\sqrt {1-x^{2}}}}}&&0<x<1\\{\frac {d}{dx}}\operatorname {arcsch} x&=-{\frac {1}{|x|{\sqrt {1+x^{2}}}}}&&x\neq 0\end{aligned}}}$

Втори изводи

И sinh и cosh се еднакви на нивните втори изводи:

${\displaystyle {\frac {d^{2}}{dx^{2}}}\sinh x=\sinh x\,}$

${\displaystyle {\frac {d^{2}}{dx^{2}}}\cosh x=\cosh x\,.}$

Сите функции со ова својство се линеарни комбинации од sinh и cosh, особено експоненцијалните функции ${\displaystyle e^{x}}$ и ${\displaystyle e^{-x}}$, нуловата функција ${\displaystyle f(x)=0}$.

Стандардни интеграли

Главна статија: Список на интеграли на хиперболични функции

${\displaystyle {\begin{aligned}\int \sinh(ax)\,dx&=a^{-1}\cosh(ax)+C\\\int \cosh(ax)\,dx&=a^{-1}\sinh(ax)+C\\\int \tanh(ax)\,dx&=a^{-1}\ln(\cosh(ax))+C\\\int \coth(ax)\,dx&=a^{-1}\ln(\sinh(ax))+C\\\int \operatorname {sech} (ax)\,dx&=a^{-1}\arctan(\sinh(ax))+C\\\int \operatorname {csch} (ax)\,dx&=a^{-1}\ln \left(\tanh \left({\frac {ax}{2}}\right)\right)+C=a^{-1}\ln \left|\operatorname {csch} (ax)-\coth(ax)\right|+C\end{aligned}}}$

Следниве интеграли може да се докажат со користење на хиперболична супституција:

${\displaystyle {\begin{aligned}\int {{\frac {1}{\sqrt {a^{2}+u^{2}}}}\,du}&=\operatorname {arsinh} \left({\frac {u}{a}}\right)+C\\\int {{\frac {1}{\sqrt {u^{2}-a^{2}}}}\,du}&=\operatorname {arcosh} \left({\frac {u}{a}}\right)+C\\\int {\frac {1}{a^{2}-u^{2}}}\,du&=a^{-1}\operatorname {artanh} \left({\frac {u}{a}}\right)+C&&u^{2}<a^{2}\\\int {\frac {1}{a^{2}-u^{2}}}\,du&=a^{-1}\operatorname {arcoth} \left({\frac {u}{a}}\right)+C&&u^{2}>a^{2}\\\int {{\frac {1}{u{\sqrt {a^{2}-u^{2}}}}}\,du}&=-a^{-1}\operatorname {arsech} \left({\frac {u}{a}}\right)+C\\\int {{\frac {1}{u{\sqrt {a^{2}+u^{2}}}}}\,du}&=-a^{-1}\operatorname {arcsch} \left|{\frac {u}{a}}\right|+C\end{aligned}}}$

каде C е интеграциона константа.

Изрази со Тејлорови редови

Горните функции може да се изразат како Тејлорови редови:

${\displaystyle \sinh x=x+{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}+{\frac {x^{7}}{7!}}+\cdots =\sum _{n=0}^{\infty }{\frac {x^{2n+1}}{(2n+1)!}}}$

Функцијата sinh x се изразува преку Тејлоров ред само со непарни експоненти на x. Значи таа е непарна функција, па −sinh x = sinh(−x), и sinh 0 = 0.

${\displaystyle \cosh x=1+{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}+{\frac {x^{6}}{6!}}+\cdots =\sum _{n=0}^{\infty }{\frac {x^{2n}}{(2n)!}}}$

Функцијата cosh x се изразува преку Тејлоров ред само со парни експоненти на x. Значи таа е парна функција, следствено, симетрична во однос на y-оската. Збирот од редовите на sinh и cosh е бесконечен ред од експоненцијалната функција.

${\displaystyle {\begin{aligned}\tanh x&=x-{\frac {x^{3}}{3}}+{\frac {2x^{5}}{15}}-{\frac {17x^{7}}{315}}+\cdots =\sum _{n=1}^{\infty }{\frac {2^{2n}(2^{2n}-1)B_{2n}x^{2n-1}}{(2n)!}},\left|x\right|<{\frac {\pi }{2}}\\\coth x&=x^{-1}+{\frac {x}{3}}-{\frac {x^{3}}{45}}+{\frac {2x^{5}}{945}}+\cdots =x^{-1}+\sum _{n=1}^{\infty }{\frac {2^{2n}B_{2n}x^{2n-1}}{(2n)!}},0<\left|x\right|<\pi \\\operatorname {sech} \,x&=1-{\frac {x^{2}}{2}}+{\frac {5x^{4}}{24}}-{\frac {61x^{6}}{720}}+\cdots =\sum _{n=0}^{\infty }{\frac {E_{2n}x^{2n}}{(2n)!}},\left|x\right|<{\frac {\pi }{2}}\\\operatorname {csch} \,x&=x^{-1}-{\frac {x}{6}}+{\frac {7x^{3}}{360}}-{\frac {31x^{5}}{15120}}+\cdots =x^{-1}+\sum _{n=1}^{\infty }{\frac {2(1-2^{2n-1})B_{2n}x^{2n-1}}{(2n)!}},0<\left|x\right|<\pi \end{aligned}}}$

каде:

${\displaystyle B_{n}\,}$ е n-тиот Бернулиев број

${\displaystyle E_{n}\,}$ е n-тиот Ојлеров број

Споредба со циркуларните функции

Тангентата на кружницата и хиперболата во (1,1) ја изразуваат геометријата на циркуларните функции во однос на површината на кружниот сектор u и хиперболичните функции кои зависат од површината на хиперболичниот сектор u.

Хиперболичните функции претставуваат проширување на тригонометријаата преку циркуларните функции. Обата вида зависат од аргумент, кој е или кружен агол или хиперболичен агол.

Бидејќи површината на кружниот сектор со полупречник r и агол u е r²u/2, истата ќе биде еднаква на u кога r = √2. На дијаграмот таквиот круг е тангента на хиперболата xy = 1 во (1,1). Жолтиот сектор претставува површина и големина на агол. Слично, жолтиот и црвениот сектор заедно претставуваат површина и агол на хиперболичниот сектор.

Краците на два правоаголни триаголници со хипотенуза на правата која ги дефинира аглите се со должина √2 пати од циркуларните и хиперболичните функции.

Хиперболичниот агол е неваријантна мерка во однос на контракцијата (хиперболична ротација), токму како што кружниот агол е непроменлив со ротацијата.^[12]

Идентитети

Хиперболичните функции задоволуваат многу идентитети и сите тие се слични по облик со тригонометриските идентитети. Всушност, Осборновото правило^[13] тврди дека секој тригонометриски идентитет може да се претвори во хиперболичен идентитет со промена на sine во sinh и cosine во cosh, и со менување на знакот на секој член која содржи производ од 2, 6, 10, 14, ... sinhs. На пример, теоремите за собирање ќе бидат

${\displaystyle {\begin{aligned}\sinh(x+y)&=\sinh(x)\cosh(y)+\cosh(x)\sinh(y)\\\cosh(x+y)&=\cosh(x)\cosh(y)+\sinh(x)\sinh(y)\\\tanh(x+y)&={\frac {\tanh(x)+\tanh(y)}{1+\tanh(x)\tanh(y)}}\end{aligned}}}$

формулите за "двоен аргумент "

${\displaystyle {\begin{aligned}\sinh(2x)&=2\sinh x\cosh x\\\cosh(2x)&=\cosh ^{2}x+\sinh ^{2}x=2\cosh ^{2}x-1=2\sinh ^{2}x+1\\\tanh(2x)&={\frac {2\tanh x}{1+\tanh ^{2}x}}\\\sinh(2x)&={\frac {2\tanh x}{1-\tanh ^{2}x}}\\\cosh(2x)&={\frac {1+\tanh ^{2}x}{1-\tanh ^{2}x}}\end{aligned}}}$

и формулите за "половина аргумент "^[14]

${\displaystyle \sinh {\frac {x}{2}}={\sqrt {{\frac {1}{2}}(\cosh x-1)}}\,}$    Забелешка: Ова е еквивалентно на неговиот циркуларен пандан помножен со −1.

${\displaystyle \cosh {\frac {x}{2}}={\sqrt {{\frac {1}{2}}(\cosh x+1)}}\,}$    Забелешка: Ова е еквивалентно на неговиот циркуларен пандан.

${\displaystyle \tanh {\frac {x}{2}}={\sqrt {\frac {\cosh x-1}{\cosh x+1}}}={\frac {\sinh x}{\cosh x+1}}={\frac {\cosh x-1}{\sinh x}}=\coth x-\operatorname {csch} x.}$

${\displaystyle \coth {\frac {x}{2}}=\coth x+\operatorname {csch} x.}$

Изводот од sinh x е cosh x, а изводот од cosh x е sinh x; ова е слично со тригонометриските функции, иако знакот е различен (извод од cos x е −sin x).

Гудермановата функција дава директна врска меѓу тригонометриските и хиперболичните функции кои не содржат комплексни броеви.

Графиконот на функција a cosh(x/a) е верижница, кривата образувана од униформен флексибилен синџир кој слободно виси помеѓу две фиксни точки под униформа гравитација.

Врска со експоненцијалната функција

Разложувањето на експоненцијалната функција на парен и непарен дел ги дава идентитетите

${\displaystyle e^{x}=\cosh x+\sinh x,}$

и

${\displaystyle e^{-x}=\cosh x-\sinh x.}$

Првиот е аналоген со Ојлеровата формула

${\displaystyle e^{ix}=\cos x+i\sin x.}$

дополнително,

${\displaystyle e^{x}={\sqrt {\frac {1+\tanh x}{1-\tanh x}}}={\frac {1+\tanh {\frac {x}{2}}}{1-\tanh {\frac {x}{2}}}}}$

Хиперболични функции за комплексни броеви

Со оглед дека експоненцијалната функција може да биде дефинирана за кој било комплексен аргумент, дефинициите на хиперболичните функции може да се прошири исто така на комплексните аргументи. Функциите sinh z и cosh z тогаш се холоморфни.

Врските со обичните тригонометриски функции се дадени со Ојлеровата формула за комплексни броеви:

${\displaystyle {\begin{aligned}e^{ix}&=\cos x+i\sin x\\e^{-ix}&=\cos x-i\sin x\end{aligned}}}$

па:

${\displaystyle {\begin{aligned}\cosh(ix)&={\frac {1}{2}}\left(e^{ix}+e^{-ix}\right)=\cos x\\\sinh(ix)&={\frac {1}{2}}\left(e^{ix}-e^{-ix}\right)=i\sin x\\\cosh(x+iy)&=\cosh(x)\cos(y)+i\sinh(x)\sin(y)\\\sinh(x+iy)&=\sinh(x)\cos(y)+i\cosh(x)\sin(y)\\\tanh(ix)&=i\tan x\\\cosh x&=\cos(ix)\\\sinh x&=-i\sin(ix)\\\tanh x&=-i\tan(ix)\end{aligned}}}$

Хиперболичните функции се периодични во однос на имагинарната компонента, со период ${\displaystyle 2\pi i}$ (${\displaystyle \pi i}$ за хиперболичен тангенс и котангенс).

Хиперболични функции во комплексната рамнина

${\displaystyle \operatorname {sinh} (z)}$	${\displaystyle \operatorname {cosh} (z)}$	${\displaystyle \operatorname {tanh} (z)}$	${\displaystyle \operatorname {coth} (z)}$	${\displaystyle \operatorname {sech} (z)}$	${\displaystyle \operatorname {csch} (z)}$

Поврзано

„Хиперболични функции“ на Ризницата ?

• е (математичка константа)
• Инверзни хиперболични функции
• Список на интеграли на хиперболични функции
• Тригонометриски функции