Тригонометриски функции

Тригонометриска функција — функција на агол. Името го добилеа по гранката од математиката која ги користи за решавање триаголници, а која се нарекува тригонометрија.

Кога аголот, знали аргументот на овие функции е реален број, тогаш тие се функции на рамнинската тригонометрија: синус и косинус, од кои се изведуваат сите останати. Од останатите основни функции на агол често во употреба се тангенс, па и котангенс, потоа, малку поретко се среќаваат косеканс и секанс, и конечно најретко синус версус и косинус версус. Кога аголот е комплексен број тогаш функциите на агол може да преминат во хиперболични функции.

Инверзните тригонометриски функции се викаат циклометриски функции и аркус-функции, т.е. функција^-1.

Дефиниции

Сл.1. Тригонометриски триаголник

Основните тригонометриски функции, синус, косинус и тангенс обично се дефинираат со помош на правоаголен триаголник (види ја сликата десно). Имено, односот на две страни во правоаголниот триаголник е функција од остриот агол на триаголникот и затоа односите меѓу страните на правоаголниот триаголник се нарекуваат тригонометриски функции. Поимот „тригонометрија“ потекнува од грчките зборови за триаголник (тригонос) и за мерење (метрео), т.е. поимот тригонометрија буквално значи „мерење на триаголникот“. Синус од остар агол во правоаголен триаголник е односот меѓу спротивната катета на тој агол и хипотенузата. Косинус од остриот агол во правоаголен триаголник е односот меѓу прилегнатата катета и хипотенузата. Тангенс е односот меѓу спротивната и прилегнатата катета на остар агол во правоаголен триаголник. Котангенс е односот меѓу прилегнатата и спротивната катета на остар агол во правоаголен триаголник.^[1]

${\displaystyle x=r\cdot \cos \phi ,\;y=r\cdot \sin \phi ,\;{\frac {y}{x}}=\operatorname {tg} \phi .}$

Позитивен математички агол има спротивна насока од стрелките на часовникот.

Тригонометриска кружница

На сликата (2) долу е прикажана кружница со полупречник еден со центар во координатниот почеток, т.е. ${\displaystyle x^{2}+y^{2}=1,}$ која се вика тригонометриска кружница.

Сл.2. Тригонометриска кружница

Дефиниција 1

Тригонометриските реални функции на агол φ се дефинираат со равенките

(а) ${\displaystyle \cos ^{2}\phi +\sin ^{2}\phi =1,\,}$ синус и косинус се реални броеви;

(б) ${\displaystyle \operatorname {tg} \phi ={\frac {\sin \phi }{\cos \phi }},\;\operatorname {ctg} \phi ={\frac {\cos \phi }{\sin \phi }},}$ тангенс и котангенс;

(в) ${\displaystyle \sec \phi ={\frac {1}{\cos \phi }},\;\csc \phi ={\frac {1}{\sin \phi }},}$ секанс и косеканс.

(г) ${\displaystyle \operatorname {vercos} \phi =1-\sin \phi ,\;\operatorname {versin} =1-\cos \phi ,}$ косинус версус и синус версус.

Функциите (в), а особено (г) ретко ги среќаваме.

Теорема 1

(а) ${\displaystyle {\overline {OA}}=\cos \phi ,\;{\overline {OC}}=\sin \phi ,}$ косинус и синус;

(б) ${\displaystyle {\overline {BE}}=\operatorname {tg} \phi ,\;{\overline {FG}}=\operatorname {ctg} \phi ,}$ тангенс и котангенс;

(в) ${\displaystyle {\overline {OE}}=\sec \phi ,\;{\overline {OG}}=\csc \phi ,}$ секанс и косеканс.

Доказ

Точката Т од сликата 1. овде (сл.2.) е точката D.

(а) Следи непосредно заради полупречникот r = 1.

(б) Да ги воочиме сличните триаголници ${\displaystyle \Delta EBO\sim \Delta DAO,}$ од каде ${\displaystyle {\overline {BE}}:{\overline {OB}}={\overline {AD}}:{\overline {OA}},}$ т.е. ${\displaystyle {\overline {BE}}:1=\sin \phi$ :\cos \phi ;} да ги воочиме сличните триаголници ${\displaystyle \Delta GFO\sim \Delta OAD,}$ одатле ${\displaystyle {\overline {FG}}:{\overline {FO}}={\overline {OA}}:{\overline {AD}},}$ т.е. ${\displaystyle {\overline {FG}}:1=\cos \phi$ :\sin \phi .}

(в) Од истите слични триаголници (б) добиваме ${\displaystyle {\overline {OE}}:{\overline {OB}}={\overline {OD}}:{\overline {OA}},}$ т.е. ${\displaystyle {\overline {OE}}:1=1:\cos \phi$ ;} потоа ${\displaystyle {\overline {OG}}:{\overline {OF}}={\overline {OD}}:{\overline {AD}},}$ т.е. ${\displaystyle {\overline {OG}}:1=1:\sin \phi .}$

Крај на доказот.

Посебни агли

Овде ќе бидат анализирани особините на вредностите на тригонометриски функции за посебни агли.

Предзнак

На претходната слика (3) претставен е Декартовиот правоаголен координатен систем и точката D на тригонометриската кружница. Аголот BOD = φ може неограничено да расте додека подвижниот крак на аголот (OD) проаѓа редум низ првиот, вториот, третиот и четвртиот квадрант, а потоа повторно по истиот круг. Значи, аголот φ може да расте до 360° и понатаму. Притоа проекциите на точката D на апсцисата и ординатата секогаш се сметаат како косинус и синус на аголот φ. Тоа значи дека косинусот е позитивен кога точката D во првиот и четвртиот квадрант, а дека синусот е позитивен кога точката D е во првиот и вториот квадрант. Детално тоа се гледа во следната табела:

Тригонометриските функции по квадранти

Квадрант	1. (0°-90°)	2. (90°-180°)	3. (180°-270°)	4. (270°-360°)
синус	+	+	-	-
косинус	+	-	-	+
тангенс	+	-	+	-

Сведување на првиот квадрант

Преку тригонометриската кружница или адиционите формули лесно може да се провери точноста на формулата за сведување на вредностите на тригонометриските функции на функции на агли од првиот квадрант:

${\displaystyle \cos(180^{o}-\phi )=-\cos \phi ,\;\sin(180^{o}-\phi )=\sin \phi ,}$

${\displaystyle \cos(180^{o}+\phi )=-\cos \phi ,\;\sin(180^{o}+\phi )=-\sin \phi ,}$

${\displaystyle \cos(-\phi )=\cos \phi ,\;\sin(-\phi )=-\sin \phi .}$

Функциите косинус и синус се периодични со основен период од 360°, a функцијата тангенс е периодична со период од 180°:

${\displaystyle \cos(360^{o}+\phi )=\cos \phi ,\;\sin(360^{o}+\phi )=\sin \phi ,\;\operatorname {tg} (180^{o}+\phi )=\operatorname {tg} \phi .}$

Периодот на синусната и косинусната функција може да се најде од формулата: ${\displaystyle T={\frac {2\pi }{\omega }}}$

Така периодот на функцијата е ${\displaystyle \sin {2\alpha }}$ еднаков ${\displaystyle T={\frac {2\pi }{2}}}$, односно ${\displaystyle \pi }$.

Функциите на агли поголеми од 360 степени со претходните формули се сведува на функции од помали агли, а потоа, ако е потребно, на првиот квадрант, на начин видлив во следната табела:

${\displaystyle \beta \,}$	${\displaystyle {\frac {\pi }{2}}+\alpha }$	${\displaystyle \pi +\alpha \,}$	${\displaystyle {\frac {3\,\pi }{2}}+\alpha }$	${\displaystyle {\frac {\pi }{2}}-\alpha }$	${\displaystyle \pi -\alpha \,}$	${\displaystyle {\frac {3\,\pi }{2}}-\alpha }$	${\displaystyle 2\,\pi -\alpha }$
${\displaystyle \sin \beta \,}$	${\displaystyle \cos \alpha \,}$	${\displaystyle -\sin \alpha \,}$	${\displaystyle -\cos \alpha \,}$	${\displaystyle \cos \alpha \,}$	${\displaystyle \sin \alpha \,}$	${\displaystyle -\cos \alpha \,}$	${\displaystyle -\sin \alpha \,}$
${\displaystyle \cos \beta \,}$	${\displaystyle -\sin \alpha \,}$	${\displaystyle -\cos \alpha \,}$	${\displaystyle \sin \alpha \,}$	${\displaystyle \sin \alpha \,}$	${\displaystyle -\cos \alpha \,}$	${\displaystyle -\sin \alpha \,}$	${\displaystyle \cos \alpha \,}$
${\displaystyle \operatorname {tg} \,\beta }$	${\displaystyle -\operatorname {ctg} \,\alpha }$	${\displaystyle \operatorname {tg} \,\alpha }$	${\displaystyle -\operatorname {ctg} \,\alpha }$	${\displaystyle \operatorname {ctg} \,\alpha }$	${\displaystyle -\operatorname {tg} \,\alpha }$	${\displaystyle \operatorname {ctg} \,\alpha }$	${\displaystyle \operatorname {tg} \,\alpha }$
${\displaystyle \operatorname {ctg} \,\beta }$	${\displaystyle -\operatorname {tg} \,\alpha }$	${\displaystyle \operatorname {ctg} \,\alpha }$	${\displaystyle -\operatorname {tg} \,\alpha }$	${\displaystyle \operatorname {tg} \,\alpha }$	${\displaystyle -\operatorname {ctg} \,\alpha }$	${\displaystyle \operatorname {tg} \,\alpha }$	${\displaystyle \operatorname {ctg} \,\alpha }$

Во општ случај тоа може да се запише вака:

${\displaystyle f(n\pi +\alpha )=\pm f(\alpha )}$

${\displaystyle f(n\pi -\alpha )=\pm f(\alpha )}$

${\displaystyle f\left({\frac {(2n+1)\pi }{2}}+\alpha \right)=\pm g(\alpha )}$

${\displaystyle f\left({\frac {(2n+1)\pi }{2}}-\alpha \right)=\pm g(\alpha )}$

Притоа f — е произволна тригонометриска функција, g — е нејзината соодветна функција (косинус за синус, синус за косинус и аналогно за останатите функции), а n — цел број.

Вредности на тригонометриските функции

Вредности на тригонометриските функции прикажани на тригонометриската кружница

За некои од аглите од првиот квадрант функциите полесно се пресметуваат:

Најчести вредности на тригонометриските функции

${\displaystyle \phi \,}$	0°	30°	45°	60°	90°
${\displaystyle \sin \phi \,}$	0	${\displaystyle {\frac {1}{2}}}$	${\displaystyle {\frac {\sqrt {2}}{2}}}$	${\displaystyle {\frac {\sqrt {3}}{2}}}$	1
${\displaystyle \cos \phi \,}$	1	${\displaystyle {\frac {\sqrt {3}}{2}}}$	${\displaystyle {\frac {\sqrt {2}}{2}}}$	${\displaystyle {\frac {1}{2}}}$	0
${\displaystyle \operatorname {tg} \phi }$	0	${\displaystyle {\frac {\sqrt {3}}{3}}}$	1	${\displaystyle {\sqrt {3}}}$	${\displaystyle \pm \infty }$

Еден од начинот на пресметување на овие вредности е прикажан во прегледот на основни агли. Од табелата се гледа дека веќе кај „основните“ агли тригонометриските функции се ирационални броеви и дека слични изрази за други агли би можело да бидат уште посложени. Поедноставен од тие посложени изрази би бил, на пример ${\displaystyle \sin 15^{o}={\frac {{\sqrt {3}}-1}{2{\sqrt {2}}}},}$ и тоа е најмалиот агол чиј синус може да се претстави со запис на проста алгебарска комбинација од рационални броеви и корени. Со векови тригонометриските вредности биле запишувани во тригонометриски таблици, на 5 до 10 децимали, a во последно време се користат скоро исклучиво сметач или калкулатор.

Вредностите на тригонометриските функции на некои агли кои се пресметуваат по нешто подолг пат се дадени во следната табела:

${\displaystyle \alpha \,}$	${\displaystyle {\frac {\pi }{12}}=15^{\circ }}$	${\displaystyle {\frac {\pi }{10}}=18^{\circ }}$	${\displaystyle {\frac {\pi }{8}}=22.5^{\circ }}$	${\displaystyle {\frac {\pi }{5}}=36^{\circ }}$	${\displaystyle {\frac {3\,\pi }{10}}=54^{\circ }}$	${\displaystyle {\frac {3\,\pi }{8}}=67.5^{\circ }}$	${\displaystyle {\frac {2\,\pi }{5}}=72^{\circ }}$
${\displaystyle \sin \alpha \,}$	${\displaystyle {\frac {{\sqrt {3}}-1}{2\,{\sqrt {2}}}}}$	${\displaystyle {\frac {{\sqrt {5}}-1}{4}}}$	${\displaystyle {\frac {\sqrt {2-{\sqrt {2}}}}{2}}}$	${\displaystyle {\frac {\sqrt {5-{\sqrt {5}}}}{2\,{\sqrt {2}}}}}$	${\displaystyle {\frac {{\sqrt {5}}+1}{4}}}$	${\displaystyle {\frac {\sqrt {2+{\sqrt {2}}}}{2}}}$	${\displaystyle {\frac {\sqrt {5+{\sqrt {5}}}}{2\,{\sqrt {2}}}}}$
${\displaystyle \cos \alpha \,}$	${\displaystyle {\frac {{\sqrt {3}}+1}{2\,{\sqrt {2}}}}}$	${\displaystyle {\frac {\sqrt {5+{\sqrt {5}}}}{2\,{\sqrt {2}}}}}$	${\displaystyle {\frac {\sqrt {2+{\sqrt {2}}}}{2}}}$	${\displaystyle {\frac {{\sqrt {5}}+1}{4}}}$	${\displaystyle {\frac {\sqrt {5-{\sqrt {5}}}}{2\,{\sqrt {2}}}}}$	${\displaystyle {\frac {\sqrt {2-{\sqrt {2}}}}{2}}}$	${\displaystyle {\frac {{\sqrt {5}}-1}{4}}}$
${\displaystyle \operatorname {tg} \,\alpha }$	${\displaystyle 2-{\sqrt {3}}}$	${\displaystyle {\sqrt {1-{\frac {2}{\sqrt {5}}}}}}$	${\displaystyle {\sqrt {\frac {{\sqrt {2}}-1}{{\sqrt {2}}+1}}}}$	${\displaystyle {\sqrt {5-2\,{\sqrt {5}}}}}$	${\displaystyle {\sqrt {1+{\frac {2}{\sqrt {5}}}}}}$	${\displaystyle {\sqrt {\frac {{\sqrt {2}}+1}{{\sqrt {2}}-1}}}}$	${\displaystyle {\sqrt {5+2\,{\sqrt {5}}}}}$
${\displaystyle \operatorname {ctg} \,\alpha }$	${\displaystyle 2+{\sqrt {3}}}$	${\displaystyle {\sqrt {5+2\,{\sqrt {5}}}}}$	${\displaystyle {\sqrt {\frac {{\sqrt {2}}+1}{{\sqrt {2}}-1}}}}$	${\displaystyle {\sqrt {1+{\frac {2}{\sqrt {5}}}}}}$	${\displaystyle {\sqrt {5-2\,{\sqrt {5}}}}}$	${\displaystyle {\sqrt {\frac {{\sqrt {2}}-1}{{\sqrt {2}}+1}}}}$	${\displaystyle {\sqrt {1-{\frac {2}{\sqrt {5}}}}}}$

Кога точката D еднаш ја обиколи кружницата поминува пат 2π односно прави 360°. Лак со должина π одговара на агол од 180° - рамен агол, π/2 е 90° - прав агол, π/3 е 60°, π/4 е 45°, π/6 е 30°, и општо лак со должина x радијани одговара на агол од 360x/2π степени. За еден радијан, х = 1, се добива агол 57,2957795... степени, т.е. во степени, минути и секунди 57°17'44,8". Еден степен има 60 минута, а една минута има 60 секунди. Изразите минути и секунди потекнуваат од латинските зборови: partes minutae primae и partes minutae secundae, т.е. први мали делови и втори мали делови. Математичките текстови за единица агол го подразбираат радијанот.

Редови

Тригонометриските функции, исто така, може да се претставуваат со (бесконечни) редови:

${\displaystyle \sin x=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+...=\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n+1}}{(2n+1)!}}}$

${\displaystyle \cos x=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}+...==\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n}}{(2n)!}}}$

Овие редови може да се употребат и за дефинирање на тригонометриски функции на комплексен број z, и хиперболични функции.

Имајќи ги предвид равенките ${\displaystyle \operatorname {tg} \,x={\frac {\sin x}{\cos x}},}$ ${\displaystyle \operatorname {ctg} \,x={\frac {\cos x}{\sin x}},}$ ${\displaystyle \sec x={\frac {1}{\cos x}}}$ и ${\displaystyle \operatorname {cosec} \,x={\frac {1}{\sin x}},}$ во Тејлоровиот ред може да се разложат следните функции:

${\displaystyle {\operatorname {tg} \,x=x+{\frac {1}{3}}\,x^{3}+{\frac {2}{15}}\,x^{5}+{\frac {17}{315}}\,x^{7}+{\frac {62}{2835}}\,x^{9}+\cdots =\sum _{n=1}^{\infty }{\frac {2^{2n}(2^{2n}-1)|B_{2n}|}{(2n)!}}x^{2n-1}\quad \left(-{\frac {\pi }{2}}<x<{\frac {\pi }{2}}\right),}}$

${\displaystyle {\operatorname {ctg} \,x={\frac {1}{x}}-{\frac {x}{3}}-{\frac {x^{3}}{45}}-{\frac {2x^{5}}{945}}-{\frac {x^{7}}{4725}}-\cdots ={\frac {1}{x}}+\sum _{n=1}^{\infty }{\frac {(-1)^{n}2^{2n}|B_{2n}|}{(2n)!}}\,x^{2n-1}\quad \left(-\pi <x<\pi \right),}}$

${\displaystyle {\sec x=1+{\frac {1}{2}}\,x^{2}+{\frac {5}{24}}\,x^{4}+{\frac {61}{720}}\,x^{6}+{\frac {277}{8064}}\,x^{8}+\cdots =1+\sum _{n=1}^{\infty }{\frac {E_{n}}{(2n)!}}\,x^{2n},\quad \left(-{\frac {\pi }{2}}<x<{\frac {\pi }{2}}\right),}}$

${\displaystyle {\csc x={\frac {1}{x}}+{\frac {1}{6}}\,x+{\frac {7}{360}}\,x^{3}+{\frac {31}{15120}}\,x^{5}+{\frac {127}{604800}}\,x^{7}+\cdots ={\frac {1}{x}}+\sum _{n=1}^{\infty }{\frac {2\,(2^{2n-1}-1)B_{n}}{(2n)!}}x^{2n-1}\quad \left(-\pi <x<\pi \right),}}$

Графикони

Тригонометриските функции може да се претстават графички. На следните слики се прикажани нивните графикони:

Графикони на тригонометриски функции: синусо, косинусо, тангенсо, секансо, косекансо, котангенсо

Парност

Косинус и секанс се парни функции, додека останатите четири се непарни функции:

${\displaystyle \sin \left(-\alpha \right)=-\sin \alpha \,,}$

${\displaystyle \cos \left(-\alpha \right)=\cos \alpha \,,}$

${\displaystyle \mathop {\mathrm {tg} } \,\left(-\alpha \right)=-\mathop {\mathrm {tg} } \,\alpha \,,}$

${\displaystyle \mathop {\mathrm {ctg} } \,\left(-\alpha \right)=-\mathop {\mathrm {ctg} } \,\alpha \,,}$

${\displaystyle \sec \left(-\alpha \right)=\sec \alpha \,,}$

${\displaystyle \mathop {\mathrm {cosec} } \,\left(-\alpha \right)=-\mathop {\mathrm {cosec} } \,\alpha \,.}$

Гранична вредност

Тетивата е пократка од лакот

На сликата лево се гледа тетивата ${\displaystyle {\overline {ADB}}}$ која сигурно е пократка од лакот ${\displaystyle {\widehat {ACB}}.}$ Тетивата е најкраткото растојание меѓу две точки на кружница. Затоа полутетивата ${\displaystyle {\overline {AD}}}$ е пократка од полулакот ${\displaystyle {\widehat {AC}}.}$ Триаголникот ODA, со остар агол ${\displaystyle alpha}$ е правоаголен. Правиот агол е во темето D, катетата ОD изнесува ${\displaystyle \cos \phi }$, катетата DA изнесува ${\displaystyle \sin \alpha }$, хипотенузата е со должина еден. Кога аголот е во радијани и ${\displaystyle 0<\alpha <{\frac {\pi }{2}},}$ тогаш

Теорема 1

${\displaystyle \lim _{\alpha \to 0}\sin \alpha =0,\;\lim _{\alpha \to 0}\cos \alpha =1.}$

Доказ: Следи од ${\displaystyle 0<\sin \phi <{\widehat {DB}}=\phi }$ и ${\displaystyle 0<1-\cos \phi <{\overline {AB}}<{\overline {DB}}<{\widehat {DB}}=\phi .}$ Крај.

Кога аголот тежи кон нула преку позитивните вредности, тогаш синусот е позитивен, а негативен е кога аголот тежи кон нула преку негативни вредности. Косинусот пак во двата случаја е позитивен. Од тоа произлегуваат лимесите за котангенс: ${\displaystyle \lim _{x\to +0}\operatorname {ctg} x=+\infty ,\;\lim _{x\to -0}\operatorname {ctg} x=-\infty .}$ Со замена на х со комплементен агол се добиваат соодветните лимеси за тангенс.

Тригонометриски круг

Теорема 2

${\displaystyle \lim _{x\to \ 0}{\frac {\sin x}{x}}=1.}$

Доказ

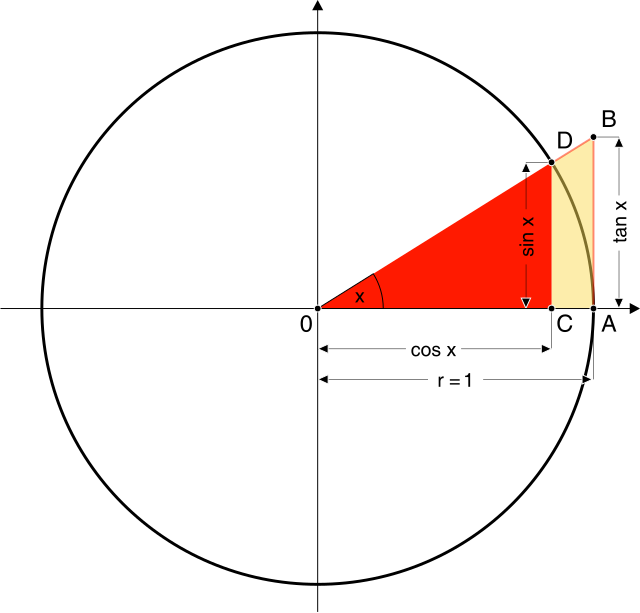
На сликата десно, површината на правоаголниот триаголник OCD е помала од површината на кружниот исечок OAD, а оваа повторно е помала од површината на правоаголниот триаголник OAB. Со х агол AOB. Оттука ${\displaystyle {\frac {\sin x\cos x}{2}}<{\frac {x}{2}}<{\frac {\operatorname {tg} x}{2}}.}$ Ако овие нееднаквости ги поделиме со (позитивен) ${\displaystyle {\frac {\sin x}{2}},}$ ќе добиеме ${\displaystyle \cos x<{\frac {x}{\sin x}}<{\frac {1}{\cos x}},}$ а оттука ${\displaystyle {\frac {1}{\cos x}}>{\frac {\sin x}{x}}>\cos x.}$ Со ${\displaystyle x\to 0}$ вреди ${\displaystyle \cos x\to 1,\;{\frac {1}{\cos x}}\to 1,}$ па е ${\displaystyle {\frac {\sin x}{x}}\to 1.}$ Синус е непарна функција па доказот за негативни агли е ист. Крај на доказот.

Извод

Извод од функцијата f(x) по дефиниција е гранична вредност: ${\displaystyle f'(x)=\lim _{\Delta x\to 0}{\frac {\Delta f(x)}{\Delta x}}=\lim _{\Delta x\to 0}{\frac {f(x+\Delta x)-f(x)}{\Delta x}}.}$

Теорема 3

(а) ${\displaystyle (\sin x)'=\cos x,\,}$

(б) ${\displaystyle (\cos x)'=-\sin x,\,}$

(в) ${\displaystyle (\operatorname {tg} x)'=\sec ^{2}x.\,}$

(г) ${\displaystyle (\operatorname {ctg} x)'=-\csc ^{2}x.\,}$

Доказ

(а) ${\displaystyle \Delta \sin x=\sin(x+\Delta x)-\sin x=2\cos \left(x+{\frac {\Delta x}{2}}\right)\sin {\frac {\Delta x}{2}},}$ па

${\displaystyle {\frac {\Delta \sin x}{\Delta x}}={\frac {\cos(x+{\frac {\Delta x}{2}})}{\frac {\Delta x}{2}}}\rightarrow \cos x,}$ када ${\displaystyle \Delta x\rightarrow 0}$ (теорема 2).

(б) Заради ${\displaystyle \cos x=\sin({\frac {\pi }{2}}-x),}$ биће ${\displaystyle (\cos x)'=\cos({\frac {\pi }{2}}-x)\cdot ({\frac {\pi }{2}}-x)'=-\cos({\frac {\pi }{2}}-x)=-\sin x.}$

(в) Извод на количник ${\displaystyle (\operatorname {tg} x)'=\left({\frac {\sin x}{\cos x}}\right)'=}$

${\displaystyle ={\frac {\sin 'x\cos x-\cos 'x\sin x}{\cos ^{2}x}}={\frac {\cos ^{2}x+\sin ^{2}x}{\cos ^{2}x}}={\frac {1}{\cos ^{2}x}}=\sec ^{2}x.}$

(г) Извод на количник ${\displaystyle (\operatorname {ctg} x)'=\left({\frac {\cos x}{\sin x}}\right)'=}$

${\displaystyle ={\frac {\cos 'x\sin x-\sin 'x\cos x}{\sin ^{2}x}}={\frac {-\sin ^{2}x-\cos ^{2}x}{\sin ^{2}x}}=-{\frac {1}{\sin ^{2}x}}=-\csc ^{2}x.}$ Крај на доказот 3.

Интеграли на тригонометриски функции

Главна статија: Список на интеграли на тригонометриски функции

Ова се интегралите на некои тригонометриски функции:

${\displaystyle \ \ \ \ f(x)}$	${\displaystyle \ \ \ \ f'(x)}$	${\displaystyle \int f(x)\,dx}$
${\displaystyle \,\ \sin x}$	${\displaystyle \,\ \cos x}$	${\displaystyle \,\ -\cos x+C}$
${\displaystyle \,\ \cos x}$	${\displaystyle \,\ -\sin x}$	${\displaystyle \,\ \sin x+C}$
${\displaystyle \,\ \tan x}$	${\displaystyle \,\ \sec ^{2}x=1+\tan ^{2}x}$	${\displaystyle -\ln \left|\cos x\right|+C}$
${\displaystyle \,\ \cot x}$	${\displaystyle \,\ -\csc ^{2}x=-(1+\cot ^{2}x)}$	${\displaystyle \ln \left|\sin x\right|+C}$
${\displaystyle \,\ \sec x}$	${\displaystyle \,\ \sec x\tan x}$	${\displaystyle \ln \left|\sec x+\tan x\right|+C}$
${\displaystyle \,\ \csc x}$	${\displaystyle \,\ -\csc x\cot x}$	${\displaystyle \ -\ln \left|\csc x+\cot x\right|+C}$

Други особини

Прегледот на скоро сите особини на тригонометриските функции кои се однесуваат на решавање на триаголници се дадени во статијата: рамнинска тригонометрија.

Во посебен прилог може да се најдат доказите за адиционите формули, каде спаѓаат и формулите за двојни агли, потоа половини агли, како и претставување на збир и разлика на тригонометриски функции со помош на производ и обратно, и изразување на останатите тригонометриски функции со помош на тангенс од половина агол.

Исто така, во посебен прилог се дадени тригонометриските равенки.

Тригонометриски функции како решенија на диференцијални равенки

Тригонометриските функции косинус и синус може да се претстават како решенија на диференцијални равенки:

${\displaystyle {\frac {d^{2}}{d\varphi ^{2}}}R(\varphi )=-R(\varphi ),}$

со почетним условом ${\displaystyle \cos(0)=\sin '(0)=1}$.

${\displaystyle \ \cos ''x=-\cos x,}$

${\displaystyle \ \sin ''x=-\sin x.}$

Тригонометриски функции како решенија на функционални равенки

Функциите косинус и синус може да се одредат како непрекинати решенија на системи функционални равенки:

${\displaystyle \left\{{\begin{array}{rcl}f(x+y)&=&f(x)f(y)-g(x)g(y)\\g(x+y)&=&g(x)f(y)+f(x)g(y)\end{array}}\right.}$

Инверзни тригонометриски функции

Главна статија: Инверзни тригонометриски функции

Инверзни тригонометриски функции се arcsin x (аркус синус икс), arccos x (аркус косинус), arctg x (аркус тангенс), arcctg x (аркус котангенс). Тие се инверзни на тригонометриските функции sin x (синус икс), cos x (косинус), tg x (тангенс), ctg x (котангенс). Претставката аркус потекнува од латинскиот збор arcus - лак, агол. Се нарекуваат и циклометриски функции.

${\displaystyle {\begin{matrix}{\mbox{за}}&-{\frac {\pi }{2}}\leq y\leq {\frac {\pi }{2}},&y=\arcsin x&{\mbox{ако}}&x=\sin y\,;\\\\{\mbox{за}}&0\leq y\leq \pi ,&y=\arccos x&{\mbox{ако}}&x=\cos y\,;\\\\{\mbox{за}}&-{\frac {\pi }{2}}<y<{\frac {\pi }{2}},&y=\arctan x&{\mbox{ако}}&x=\tan y\,;\\\\{\mbox{за}}&-{\frac {\pi }{2}}\leq y\leq {\frac {\pi }{2}},y\neq 0,&y=\operatorname {arccsc} x&{\mbox{ако}}&x=\csc y\,;\\\\{\mbox{за}}&0\leq y\leq \pi ,y\neq {\frac {\pi }{2}},&y=\operatorname {arcsec} x&{\mbox{ако}}&x=\sec y\,;\\\\{\mbox{за}}&0<y<\pi ,&y=\operatorname {arccot} x&{\mbox{ако}}&x=\cot y\,.\end{matrix}}}$

Примена во физиката

Примената на тригонометријата и тригонометриските функции во физиката е многу голема.

Така на пример доста се користат во анализа на простирањето на брановите, опишување на хармониските осцилации како периодични движења, претставување на наизменичната струја, итн.