Удлинённая треугольная мозаика

Удлинённая треугольная мозаика — это полуправильная мозаика на евклидовой плоскости. Мозаика имеет три треугольника и два квадрата при каждой вершине. Мозаика называется треугольной мозаикой, удлинённой рядами квадратов, и она имеет символ Шлефли {3,6}:e.

Удлинённая треугольная мозаика
Тип	Полуправильная мозаика
Конфигурация вершины	3.3.3.4.4
Символ Шлефли	{3,6}:e s{∞}h1{∞}
Символ Витхоффа	2 | 2 (2 2)
Симметрии	cmm, [∞,2+,∞], (2*22)
Диаграммы Коксетера — Дынкина
Двойственная мозаика	Призматическая пятиугольная мозаика
Акроним Бауэрса	Etrat
Свойства	изогональная

Конвей назвал эту мозаику isosnub quadrille (изокурносый квадропаркет)^[1].

Имеется 3 правильных и 8 полуправильных мозаик на плоскости. Эта мозаика похожа на плосконосую квадратную мозаику, которая также имеет 3 треугольника и два квадрата в каждой вершине, но порядок элементов другой.

Построение

Мозаика является единственной выпуклой однородной мозаикой, которая не может быть создана с помощью построения Витхоффа. Она может быть построена как чередующиеся слои бесконечноугольных призм^[англ.] и бесконечноугольных антипризм^[англ.].

Однородные раскраски

Существует одна однородная раскраска удлинённой треугольной мозаики. Две 2-однородных раскраски имеют одну вершинную фигуру, 11123, и два цвета квадратов, но они не являются 1-однородными. Строки повторяются либо отражением, либо скользящим отражением и в общем случае каждая строка квадратов может быть сдвинута независимо. 2-Однородные мозаики называются также архимедовыми раскрасками. Имеется бесконечное число вариантов этих архимедовых раскрасок с произвольными сдвигами в цветах строки квадратов.

11122 (1-uniform)	11123 (2-однородная или 1-архимедова)
cmm (2*22)	pmg (22*)	pgg (22×)

Упаковка окружностей

Удлинённая треугольная мозаика может быть использована для упаковки кругов, если располагать круги одинакового диаметра с центрами в каждой вершине. Каждый круг касается 5 других кругов в упаковке (контактное число)^[2].

Связанные мозаики

Сектора слоёв треугольников и квадратов могут быть комбинированы в радиальные формы. Такая конструкция смешивает две конфигурации вершин, 3.3.3.4.4 и 3.3.4.3.4 на переходах. Чтобы замостить плоскость с различной концигурацией центра, нужно двенадцать секторов. Двойственные мозаики образуются пятиугольниками каирской пятиугольной мозаики^[3].

Примеры радиальных форм

Центр	Треугольник		Квадрат		Шестиугольник
Симметрия	[3]	[3]+	[2]	[4]+	[6]	[6]+
Tower
Dual

Варианты симметрии

Мозаика является первой в серии вариантов симметрии^[4] гиперболических однородных мозаик с симметрией 2*n2 в орбифолдной нотации^[англ.], вершинной фигурой 4.n.4.3.3.3 и диаграммой Коксетера — Дынкина . Их двойственные мозаики имеют шестиугольные грани в гиперболической плоскости с конфигурацией грани V4.n.4.3.3.3.

Варианты симметрии 2*n2 однородных мозаик: 4.n.4.3.3.3

4.2.4.3.3.3	4.3.4.3.3.3	4.4.4.3.3.3
2*22	2*32	2*42
	или	или

Существует четыре связанных 2-однородных мозаики^[англ.], с 2 или 3 рядами треугольников или квадратов^[5][6].

Дважды удлинённая	Трижды удлинённая	Наполовину удлинённая	На треть удлинённая

Призматическая пятиугольная мозаика

Призматическая пятиугольная мозаика
Тип	Двойственная однородная мозаика
Группа орнамента	cmm, [∞,2+,∞], (2*22)
Диаграммы Коксетера — Дынкина
Двойственная мозаика	Удлинённая треугольная мозаика
Свойства	изоэдральная
Грани	неправильные пятиугольники V3.3.3.4.4

Призматическая пятиугольная мозаика — это двойственная однородная мозаика на евклидовой плоскости. Это одна из 15 известных изодральных пятиугольных мозаик. Она может рассматриваться как растянутый шестиугольный паркет со множеством параллельных секущих прямых через шестиугольники.

Конвей назвал эту мозаику iso(4-)pentille (изо(4-)пятипаркетом)^[7]. Каждая из пятиугольных граней мозаики имеет три угла в 120° и два в 90°.

Мозаика связана с каирской пятиугольной мозаикой с конфигурацией грани V3.3.4.3.4.

Геометрические варианты

Пятиугольный паркет из одной выпуклой плитки типа 6 имеет ту же топологию, но две длины рёбер и меньшую по симметрии группу орнамента p2 (2222):

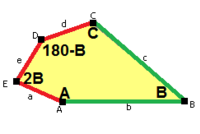a=d=e, b=c B+D=180°, 2B=E

Связанные 2-однородные двойственные мозаики

Имеется четыре связанные 2-однородные двойственные мозаики с рядами квадратов или шестиугольников.

Двойственные: Дважды удлинённая	Двойственные: Трижды удлинённая	Двойственные: Наполовину удлинённая	Двойственные: Удлинённая на треть
Двойственные: [44; 33.42]1 (t=2,e=4)	Двойственные: [44; 33.42]2 (t=3,e=5)	Двойственные: [36; 33.42]1 (t=3,e=4)	Двойственные: [36; 33.42]2 (t=4,e=5)

См. также

• Мозаики из выпуклых правильных многоугольников на евклидовой плоскости
• Удлинённые треугольные призматические соты
• Скрученно удлинённые призматические соты