Мозаики из выпуклых правильных многоугольников на евклидовой плоскости

Замощения евклидовой плоскости выпуклыми правильными многоугольниками широко использовался ещё с античных времён. Первое систематическое изложение было сделано Кеплером в его книге Harmonices Mundi (Гармония мира, на латинском, 1619).

Примеры периодических мозаик

Правильная мозаика имеет один вид правильной грани.	Полуправильная или однородная мозаика имеет один тип вершины, но два и более видов граней.
k-однородная мозаика имеет k вида вершин и два или более видов правильных граней.	Мозаики, не соединённые ребро-к-ребру, могут иметь различные размеры правильных граней

Правильные мозаики

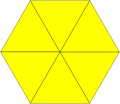
Согласно Грюнбауму и Шепарду^[англ.], говорят, что мозаика правильная, если группа симметрии мозаики действует транзитивно на флаги мозаики, где флаг — это тройка, состоящая из взаимно смежных вершин, рёбер и плиток мозаики. Это означает, что для любой пары флагов существует операция симметрии, переводящая первый флаг во второй. Это эквивалентно мозаике соединённых ребро-к-ребру конгруэнтных правильных многоугольников. Должно быть шесть правильных треугольников, четыре квадрата или три правильных шестиугольника в каждой вершине, откуда получаем три правильных замощения.

Правильные мозаики (3)

p6m, *632		p4m, *442
36 (t=1, e=1)	63 (t=1, e=1)	44 (t=1, e=1)

Архимедовы, однородные, или полуправильные мозаики

Дополнительные сведения: Список выпуклых однородных мозаик

Вершинная транзитивность означает, что для любой пары вершин существует симметрия (параллельный перенос также включается в симметрии), отображающая первую вершину во вторую ^[1].

Если требование транзитивности флагов ослаблено до транзитивности вершин, но условие соединения плиток ребро-к-ребру сохраняется, существует восемь дополнительных мозаик, которые известны как архимедовы, однородные, или полуправильные. Заметим, что существует две зеркальные (энантиоморфные или хиральные) формы 3⁴.6 (плосконосых шестиугольных) мозаик и обе показаны в таблице ниже. Все остальные правильные и полуправильные мозаики ахиральны.

Однородные мозаики (8)

p6m, *632
3.122[англ.] (t=2, e=2)	3.4.6.4[англ.] (t=3, e=2)	4.6.12[англ.] (t=3, e=3)	(3.6)2 (t=2, e=1)
p4m, *442	p4, 442	cmm, 2*22	p6, 632
4.82 (t=2, e=2)	32.4.3.4 (t=2, e=2)	33.42[англ.] (t=2, e=3)	Плосконосая шестиугольная мозаика (t=3, e=3)

Грюнбаум и Шепард эти мозаики называют архимедовыми, как указание на локальность свойства расположения плиток вокруг вершин, для отличия от однородных, для которых вершинная транзитивность является глобальным свойством. Хотя на плоскости этими двумя свойствами обладают все мозаики, в других пространствах существуют архимедовы мозаики, не являющиеся однородными.

k-однородные мозаики

3-однородная мозаика с номером #57 из 61

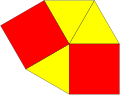
Как изотоксальная, жёлтые треугольники, красные квадраты

Как 4-изоэдральная, 3 цвета для треугольников

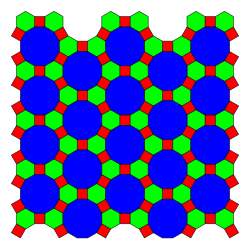
Такие периодические мозаики можно классифицировать числом орбит вершин, рёбер и плиток. Если существует ${\displaystyle k}$ орбит вершин, мозаика считается ${\displaystyle k}$-однородной или ${\displaystyle k}$-изогональной (равноугольной). Если существует ${\displaystyle t}$ орбит плиток, мозаика считается ${\displaystyle t}$-изоэдральной. Если существует ${\displaystyle e}$ орбит рёбер, мозаика считается ${\displaystyle e}$-изотоксальной (рёберно-транзитивный).

k-однородные мозаики с одинаковыми вершинными фигурами можно далее идентифицировать их симметрией группы обоев.

1-однородные мозаики включают 3 правильные мозаики и 8 полуправильных с 2 или более видами правильных многоугольных граней. Существует 20 2-однородных мозаик, 61 3-однородных мозаик, 151 4-однородных мозаик, 332 5-однородных мозаик и 673 6-однородных мозаик. Все мозаики можно сгруппировать числом m различных фигур, которые называются m-архимедовыми мозаиками ^[2]

Число k-однородных m-архимедовых мозаик

	m
k		1	2	3	4	5	6	7	8	9	Всего
	1	11	0	0	0	0	0	0	0	0	11
	2	0	20	0	0	0	0	0	0	0	20
	3	0	22	39	0	0	0	0	0	0	61
	4	0	33	85	33	0	0	0	0	0	151
	5	0	74	149	94	15	0	0	0	0	332
	6	0	100	284	187	92	10	0	0	0	673
	7	?	?	?	?	?	?	7	0	0	?
	8	?	?	?	?	?	?	20	0	0	?
	9	?	?	?	?	?	?	?	8	0	?
	10	?	?	?	?	?	?	?	27	0	?
	11	?	?	?	?	?	?	?	?	1	?

Другие типы вершин в мозаик евклидовой плоскости

Для евклидовых мозаик с соединением ребро-к-ребру внутренние углы многоугольников должны в сумме давать 360º. Правильный ${\displaystyle n}$-угольник имеет внутренний угол ${\displaystyle \left(1-{\frac {2}{n}}\right)180^{\circ }}$ . Существует семнадцать комбинаций правильных многоугольников, сумма внутренних углов которых равна 360º, каждая из которых называется видом вершины. В четырёх случаях существует два различных циклических порядка многоугольников, дающие двадцать один вид вершин.

Только одиннадцать из них могут появиться в однородной мозаике правильных многоугольников, приведённых в предыдущих разделах.

В частности, если три многоугольника встречаются в вершине и один имеет нечётное число сторон, два других многоугольника должны быть теми же самыми. В противном случае они должны поочерёдно окружать первый многоугольник, что невозможно при нечётной стороне сторон. Согласно этим ограничениям следующие шесть вариантов не могут присутствовать в какой-либо мозаике правильных многоугольников:

3 многоугольника в вершинах (неиспользуемые)

3.7.42[англ.]

3.8. 24

3.9. 18

3.10. 15

4.5. 20

5.5.10

Эти четыре могут быть использованы в k-однородных мозаик:

4 многоугольника в вершине (могут присутствовать вместе с другими видами вершин)

Допустимые виды вершин	32.4.12	3.4.3.12	32.62	3.42.6
Примеры 2-однородных мозаик	с 36	с 3.12.12	с (3.6)2	с (3.6)2

Разрезанные правильные многоугольники

Некоторые из k-однородных мозаик могут быть получены с помощью симметричного разрезания плитки мозаики внутренними рёбрами, например:

Разрезанные многоугольники рёбрами,
равными рёбрам исходного многоуольника

Шестиугольник	Двенадцатиугольник

Некоторые k-однородные многоугольники могут быть получены разрезанием правильных многоугольников с новыми вершинами на исходных рёбрах, например:

Разрезание с 1 или 2 вершин на ребре

треугольник			квадрат		шестиугольник

2-однородные мозаики

Существует двадцать 2-однородных мозаик евклидовой плоскости (называемых также 2-изогональными мозаиками или полуправильными мозаиками) ^[3][4][5].

2-однородные мозаики (20)

p6m, *632						p4m, *442
[36; 32.4.3.4][англ.] (t=3, e=3)	[3.4.6.4; 32.4.3.4] (t=4, e=4)	[3.4.6.4; 33.42] (t=4, e=4)	[3.4.6.4; 3.42.6] (t=5, e=5)	[4.6.12; 3.4.6.4][англ.] (t=4, e=4)	[36; 32.4.12][англ.] (t=4, e=4)	[3.12.12; 3.4.3.12] (t=3, e=3)
p6m, *632	p6, 632	p6, 632	cmm, 2*22	pmm, *2222	cmm, 2*22	pmm, *2222
[36; 32.62] (t=2, e=3)	[36; 34.6]1 (t=3, e=3)	[36; 34.6]2 (t=5, e=7)	[32.62; 34.6] (t=2, e=4)	[3.6.3.6; 32.62] (t=2, e=3)	[3.42.6; 3.6.3.6][англ.]2 (t=3, e=4)	[3.42.6; 3.6.3.6]1 (t=4, e=4)
p4g, 4*2	pgg, 2×	cmm, 2*22	cmm, 2*22	pmm, *2222	cmm, 2*22
[33.42; 32.4.3.4]1 (t=4, e=5)	[33.42; 32.4.3.4]2 (t=3, e=6)	[44; 33.42]1 (t=2, e=4)	[44; 33.42]2 (t=3, e=5)	[36; 33.42]1 (t=3, e=4)	[36; 33.42]2 (t=4, e=5)

3-однородные мозаики

Существует 61 3-однородная мозаика евклидовой плоскости. 39 являются 3-архимедовыми с 3 различными видами вершин, а 22 имеет 2 одинаковые виды вершин в различных орбитах симметрии^[6].

3-однородные мозаики, 3 вида вершин

3-однородные мозаики с 3 видами вершин (39)

[3.426; 3.6.3.6; 4.6.12] (t=6, e=7)	[36; 324.12; 4.6.12] (t=5, e=6)	[324.12; 3.4.6.4; 3.122] (t=5, e=6)	[3.4.3.12; 3.4.6.4; 3.122] (t=5, e=6)	[3342; 324.12; 3.4.6.4] (t=6, e=8)
[36; 3342; 324.12] (t=6, e=7)	[36; 324.3.4; 324.12] (t=5, e=6)	[346; 3342; 324.3.4] (t=5, e=6)	[36; 324.3.4; 3.426] (t=5, e=6)	[36; 324.3.4; 3.4.6.4] (t=5, e=6)
[36; 3342; 3.4.6.4] (t=6, e=6)	[36; 324.3.4; 3.4.6.4] (t=6, e=6)	[36; 3342; 324.3.4] (t=4, e=5)	[324.12; 3.4.3.12; 3.122] (t=4, e=7)	[3.4.6.4; 3.426; 44] (t=3, e=4)
[324.3.4; 3.4.6.4; 3.426] (t=4, e=6)	[3342; 324.3.4; 44] (t=4, e=6)	[3.426; 3.6.3.6; 44] (t=5, e=7)	[3.426; 3.6.3.6; 44] (t=6, e=7)	[3.426; 3.6.3.6; 44] (t=4, e=5)
[3.426; 3.6.3.6; 44] (t=5, e=6)	[3342; 3262; 3.426] (t=5, e=8)	[3262; 3.426; 3.6.3.6] (t=4, e=7)	[3262; 3.426; 3.6.3.6] (t=5, e=7)	[346; 3342; 3.426] (t=5, e=7)
[3262; 3.6.3.6; 63] (t=4, e=5)	[3262; 3.6.3.6; 63] (t=2, e=4)	[346; 3262; 63] (t=2, e=5)	[36; 3262; 63] (t=2, e=3)	[36; 346; 3262] (t=5, e=8)
[36; 346; 3262] (t=3, e=5)	[36; 346; 3262] (t=3, e=6)	[36; 346; 3.6.3.6] (t=5, e=6)	[36; 346; 3.6.3.6] (t=4, e=4)	[36; 346; 3.6.3.6] (t=3, e=3)
[36; 3342; 44] (t=4, e=6)	[36; 3342; 44] (t=5, e=7)	[36; 3342; 44] (t=3, e=5)	[36; 3342; 44] (t=4, e=6)

3-однородные мозаики, 2 вида вершин (2:1)

3-однородные мозаики (2:1) (22)

[(3.4.6.4)2; 3.426] (t=6, e=6)	[(36)2; 346] (t=3, e=4)	[(36)2; 346] (t=5, e=5)	[(36)2; 346] (t=7, e=9)	[36; (346)2] (t=4, e=6)
[36; (324.3.4)2] (t=4, e=5)	[(3.426)2; 3.6.3.6] (t=6, e=8)	[3.426; (3.6.3.6)2] (t=4, e=6)	[3.426; (3.6.3.6)2] (t=5, e=6)	[3262; (3.6.3.6)2] (t=3, e=5)
[(346)2; 3.6.3.6] (t=4, e=7)	[(346)2; 3.6.3.6] (t=4, e=7)	[3342; (44)2] (t=4, e=7)	[(3342)2; 44] (t=5, e=7)	[3342; (44)2] (t=3, e=6)
[(3342)2; 44] (t=4, e=6)	[(3342)2; 324.3.4] (t=5, e=8)	[3342; (324.3.4)2] (t=6, e=9)	[36; (3342)2] (t=5, e=7)	[36; (3342)2] (t=4, e=6)
[(36)2; 3342] (t=6, e=7)	[(36)2; 3342] (t=5, e=6)

4-однородные мозаики

Существует 151 4-однородная мозаика евклидовой плоскости. Исследования Брайана Гейлбаха (Brian Galebach) воспроизвели список Кротенхирдта (Krotenheerdt) из 33 4-однородных мозаик с 4 различными видами вершин, 85 мозаик с 3 видами вершин и 33 мозаики с 2 видами вершин.

4-однородные мозаики, 4 вида вершин

Существует 34 мозаики с 4 видами вершин.

4-однородные мозаики с 4 видами вершин (33)

[33434; 3262; 3446; 63]	[3342; 3262; 3446; 46.12]	[33434; 3262; 3446; 46.12]	[36; 3342; 33434; 334.12]	[36; 33434; 334.12; 3.122]
[36; 33434; 343.12; 3.122]	[36; 3342; 33434; 3464]	[36; 3342; 33434; 3464]	[36; 33434; 3464; 3446]	[346; 3262; 3636; 63]
[346; 3262; 3636; 63]	[334.12; 343.12; 3464; 46.12]	[3342; 334.12; 343.12; 3.122]	[3342; 334.12; 343.12; 44]	[3342; 334.12; 343.12; 3.122]
[36; 3342; 33434; 44]	[33434; 3262; 3464; 3446]	[36; 3342; 3446; 3636]	[36; 346; 3446; 3636]	[36; 346; 3446; 3636]
[36; 346; 3342; 3446]	[36; 346; 3342; 3446]	[36; 346; 3262; 63]	[36; 346; 3262; 63]	[36; 346; 3262; 63]
[36; 346; 3262; 63]	[36; 346; 3262; 3636]	[3342; 3262; 3446; 63]	[3342; 3262; 3446; 63]	[3262; 3446; 3636; 44]
[3262; 3446; 3636; 44]	[3262; 3446; 3636; 44]	[3262; 3446; 3636; 44]

4-однородные мозаики, 3 вида вершин (2:1:1)

Существует 85 мозаик с 3 видами вершин.

4-однородные мозаики (3:1)

[3464; (3446)2; 46.12]	[3464; 3446; (46.12)2]	[334.12; 3464; (3.122)2]	[343.12; 3464; (3.122)2]	[33434; 343.12; (3464)2]
[(36)2; 3342; 334.12]	[(3464)2; 3446; 3636]	[3464; 3446; (3636)2]	[3464; (3446)2; 3636]	[(36)2; 3342; 33434]
[(36)2; 3342; 33434]	[36; 3262; (63)2]	[36; 3262; (63)2]	[36; (3262)2; 63]	[36; (3262)2; 63]
[36; 3262; (63)2]	[36; 3262; (63)2]	[36; (346)2; 3262]	[36; (3262)2; 3636]	[(346)2; 3262; 63]
[(346)2; 3262; 63]	[346; 3262; (3636)2]	[346; 3262; (3636)2]	[3342; 33434; (3464)2]	[36; 33434; (3464)2]
[36; (33434)2; 3464]	[36; (3342)2; 3464]	[(3464)2; 3446; 3636]	[346; (33434)2; 3446]	[36; 3342; (33434)2]
[36; 3342; (33434)2]	[(3342)2; 33434; 44]	[(3342)2; 33434; 44]	[3464; (3446)2; 44]	[33434; (334.12)2; 343.12]
[36; (3262)2; 63]	[36; (3262)2; 63]	[36; 346; (3262)2]	[(36)2; 346; 3262]	[(36)2; 346; 3262]
[(36)2; 346; 3636]	[346; (3262)2; 3636]	[346; (3262)2; 3636]	[(346)2; 3262; 3636]	[(346)2; 3262; 3636]
[36; 346; (3636)2]	[3262; (3636)2; 63]	[3262; (3636)2; 63]	[(3262)2; 3636; 63]	[3262; 3636; (63)2]
[346; 3262; (63)2]	[346; (3262)2; 3636]	[3262; 3446; (3636)2]	[3262; 3446; (3636)2]	[346; (3342)2; 3636]
[346; (3342)2; 3636]	[346; 3342; (3446)2]	[3446; 3636; (44)2]	[3446; 3636; (44)2]	[3446; 3636; (44)2]
[3446; 3636; (44)2]	[(3446)2; 3636; 44]	[(3446)2; 3636; 44]	[(3446)2; 3636; 44]	[(3446)2; 3636; 44]
[(3446)2; 3636; 44]	[(3446)2; 3636; 44]	[(3446)2; 3636; 44]	[(3446)2; 3636; 44]	[3446; (3636)2; 44]
[3446; (3636)2; 44]	[3446; (3636)2; 44]	[3446; (3636)2; 44]	[36; 3342; (44)2]	[36; 3342; (44)2]
[36; (3342)2; 44]	[36; 3342; (44)2]	[36; 3342; (44)2]	[36; (3342)2; 44]	[36; (3342)2; 44]
[36; (3342)2; 44]	[(36)2; 3342; 44]	[(36)2; 3342; 44]	[(36)2; 3342; 44]	[(36)2; 3342; 44]

4-однородные мозаики, 2 вида вершин (2:2) и (3:1)

Существует 33 мозаики с 2 видами вершин, 12 с отношением типов плиток 2:2 и 21 с отношением (3:1).

4-однородные мозаики (2:2)

[(3464)2; (46.12)2]	[(33434)2; (3464)2]	[(33434)2; (3464)2]	[(346)2; (3636)2]	[(36)2; (346)2]
[(3342)2; (33434)2]	[(3342)2; (44)2]	[(3342)2; (44)2]	[(3342)2; (44)2]	[(36)2; (3342)2]
[(36)2; (3342)2]	[(36)2; (3342)2]

4-однородные мозаики (3:1)

[343.12; (3.122)3]	[(346)3; 3636]	[36; (346)3]	[(36)3; 346]	[(36)3; 346]
[(3342)3; 33434]	[3342; (33434)3]	[3446; (3636)3]	[3446; (3636)3]	[3262; (3636)3]
[3262; (3636)3]	[3342; (44)3]	[3342; (44)3]	[(3342)3; 44]	[(3342)3; 44]
[(3342)3; 44]	[36; (3342)3]	[36; (3342)3]	[36; (3342)3]	[(36)3; 3342]
[(36)3; 3342]

5-однородные мозаики

Существует 332 5-однородные мозаики евклидовой плоскости. Исследования Брайана Гейлбаха дали 332 5-однородных мозаик с числом видов вершин от 2 до 5. Существует 74 мозаики с 2 видами вершин, 149 мозаик с 3 видами вершин, 94 мозаики с 4 видами вершин и 15 с 5 видами вершин.

5-однородные мозаики, 5 типов вершин

Существует 15 5-однородных мозаик с 5 видами вершинных фигур.

5-однородные мозаики, 5 типов

[33434; 3262; 3464; 3446; 63]	[36; 346; 3262; 3636; 63]	[36; 346; 3342; 3446; 46.12]	[346; 3342; 33434; 3446; 44]	[36; 33434; 3464; 3446; 3636]
[36; 346; 3464; 3446; 3636]	[33434; 334.12; 3464; 3.12.12; 46.12]	[36; 346; 3446; 3636; 44]	[36; 346; 3446; 3636; 44]	[36; 346; 3446; 3636; 44]
[36; 346; 3446; 3636; 44]	[36; 3342; 3446; 3636; 44]	[36; 346; 3342; 3446; 44]	[36; 3342; 3262; 3446; 3636]	[36; 346; 3342; 3262; 3446]

5-однородные мозаики, 4 типов вершин (2:1:1:1)

Существует 94 5-однородные мозаики с 4 видами вершин.

5-однородные мозаики (2:1:1:1)

[36; 33434; (3446)2; 46.12]	[36; 33434; 3446; (46.12)2]	[36; 33434; 3464; (46.12)2]	[36; 3342; (334.12)2; 3464]	[36; (3342)2; 334.12; 3464]
[36; 33434; (334.12)2; 3464]	[36; 33434; 334.12; (3.12.12)2]	[36; 346; (3342)2; 334.12]	[36; 33434; 343.12; (3.12.12)2]	[(3342)2; 334.12; 343.12; 3.12.12]
[(3342)2; 334.12; 343.12; 3.12.12]	[(3342)2; 334.12; 343.12; 44]	[33434; 3262; (3446)2; 44]	[36; (3342)2; 33434; 44]	[346; (3342)2; 33434; 44]
[36; 3342; (3464)2; 3446]	[3342; 3262; 3464; (3446)2]	[33434; 3262; 3464; (3446)2]	[36; 33434; (3446)2; 3636]	[3342; 33434; 3464; (3446)2]
[36; 33434; (3262)2; 3446]	[3342; 3262; (3464)2; 3446]	[33434; 3262; (3464)2; 3446]	[346; 3342; (3464)2; 3446]	[36; (3342)2; 33434; 3464]
[36; (3342)2; 33434; 3464]	[36; 3342; (33434)2; 3464]	[(36)2; 3342; 33434; 3464]	[36; 3342; (33434)2; 3464]	[(36)2; 3342; 33434; 334.12]
[36; 33434; (334.12)2; 343.12]	[(36)2; 346; 3342; 33434]	[(36)2; 346; 3262; 63]	[36; (346)2; 3262; 63]	[(36)2; 346; 3262; 3636]
[36; 346; (3262)2; 3636]	[36; (346)2; 3262; 3636]	[(36)2; 346; 3262; 3636]	[36; 346; 3262; (3636)2]	[36; (346)2; 3262; 3636]
[36; (346)2; 3262; 3636]	[36; (346)2; 3262; 3636]	[36; 346; (3262)2; 3636]	[36; 346; (3262)2; 3636]	[36; 346; 3262; (63)2]
[36; 346; (3262)2; 63]	[346; (3262)2; 3636; 63]	[(346)2; 3262; 3636; 63]	[(36)2; 346; 3262; 63]	[(36)2; 346; 3262; 63]
[36; 346; 3262; (63)2]	[36; 346; 3262; (63)2]	[36; 346; 3262; (63)2]	[36; 346; (3262)2; 63]	[346; (3262)2; 3636; 63]
[346; (3262)2; 3636; 63]	[346; (3262)2; 3636; 63]	[346; 3262; 3636; (63)2]	[346; (3262)2; 3636; 63]	[3342; 3262; 3446; (63)2]
[3342; 3262; 3446; (63)2]	[3262; 3446; 3636; (44)2]	[3262; 3446; 3636; (44)2]	[3262; 3446; (3636)2; 44]	[3262; 3446; (3636)2; 44]
[3342; 3262; 3446; (44)2]	[346; 3342; 3446; (44)2]	[3262; 3446; 3636; (44)2]	[3262; 3446; 3636; (44)2]	[3262; 3446; (3636)2; 44]
[3262; 3446; (3636)2; 44]	[3342; 3262; 3446; (44)2]	[346; 3342; 3446; (44)2]	[346; (3342)2; 3636; 44]	[36; 3342; (3446)2; 3636]
[346; (3342)2; 3446; 3636]	[346; (3342)2; 3446; 3636]	[(36)2; 346; 3446; 3636]	[36; 3342; (3446)2; 3636]	[346; (3342)2; 3446; 3636]
[346; (3342)2; 3446; 3636]	[(36)2; 346; 3446; 3636]	[(36)2; 3342; 3446; 3636]	[36; 3342; 3446; (3636)2]	[346; 3342; (3446)2; 3636]
[36; 346; (3342)2; 3446]	[346; (3342)2; 3262; 3636]	[346; (3342)2; 3262; 3636]	[36; (346)2; 3342; 3446]	[36; (346)2; 3342; 3446]
[36; (346)2; 3342; 3446]	[36; 346; (3342)2; 3262]	[(36)2; 346; 3342; 3636]	[(36)2; 346; 3342; 3636]

5-однородные мозаики, 3 типа вершин (3:1:1) и (2:2:1)

Существует 149 5-однородных мозаик с тремя видами вершин, из них у 60 виды вершин находятся в отношении 3:1:1 и 89 имеют отношение 2:2:1.

5-однородные мозаики (3:1:1)

[36; 334.12; (46.12)3]	[(36)2; (3342)2; 3464]	[(3342)2; 334.12; (3464)2]	[36; (33434)2; (3464)2]	[3342; (33434)2; (3464)2]
[3342; (33434)2; (3464)2]	[3342; (33434)2; (3464)2]	[(33434)2; 343.12; (3464)2]	[3464; 3446; (46.12)3]	[36; (334.12)3; 46.12]
[334.12; 343.12; (3.12.12)3]	[36; (33434)3; 343.12]
[3262; 3636; (63)3]	[346; 3262; (63)3]	[36; (3262)3; 63]	[36; (3262)3; 63]	[3262; (3636)3; 63]
[3446; 3636; (44)3]	[3446; 3636; (44)3]	[36; 3342; (44)3]	[36; 3342; (44)3]	[3446; (3636)3; 44]
[3446; (3636)3; 44]	[36; (3342)3; 44]	[36; (3342)3; 44]	[36; (3342)3; 44]	[(36)3; 3342; 44]
[(36)3; 3342; 44]	[3446; 3636; (44)3]	[3446; 3636; (44)3]	[36; 3342; (44)3]	[36; 3342; (44)3]
[(3342)3; 3262; 3446]	[3262; 3446; (3636)3]	[3262; 3446; (3636)3]	[3262; 3446; (3636)3]	[3262; 3446; (3636)3]
[3446; (3636)3; 44]	[3446; (3636)3; 44]	[36; (3342)3; 44]	[36; (3342)3; 44]	[36; (3342)3; 44]
[(36)3; 3342; 44]	[(36)3; 3342; 44]	[36; (3342)3; 44]	[36; (3342)3; 44]	[36; (3342)3; 44]
[(3342)3; 3446; 3636]	[(3342)3; 3446; 3636]	[346; (3342)3; 3446]	[(36)3; 346; 3262]	[(36)3; 346; 3262]
[(36)3; 346; 3262]	[346; (3262)3; 3636]	[346; (3262)3; 3636]	[(346)3; 3262; 3636]	[(346)3; 3262; 3636]
[(36)3; 346; 3262]	[(36)3; 346; 3262]	[(346)3; 3262; 3636]	[36; 346; (3636)3]	[36; 346; (3636)3]
[36; 346; (3636)3]	[36; 346; (3636)3]	[(36)3; 346; 3636]	[(36)3; 346; 3636]	[36; (346)3; 3636]

5-однородные мозаики (2:2:1)

[(3446)2; (3636)2; 46.12]	[36; (3262)2; (63)2]	[(3262)2; (3636)2; 63]	[(346)2; (3262)2; 63]	[36; (3262)2; (63)2]
[(36)2; (3342)2; 33434]	[(36)2; 3342; (33434)2]	[346; (3342)2; (33434)2]	[(36)2; 3342; (33434)2]	[(36)2; 3342; (33434)2]
[(3262)2; 3636; (63)2]	[(3446)2; 3636; (44)2]	[(3446)2; 3636; (44)2]	[3446; (3636)2; (44)2]	[(3446)2; 3636; (44)2]
[(3446)2; 3636; (44)2]	[3446; (3636)2; (44)2]	[36; (3342)2; (44)2]	[(36)2; 3342; (44)2]	[(36)2; 3342; (44)2]
[(3446)2; 3636; (44)2]	[(3446)2; 3636; (44)2]	[(3446)2; 3636; (44)2]	[(3446)2; 3636; (44)2]	[(3446)2; 3636; (44)2]
[36; (3342)2; (44)2]	[(36)2; (3342)2; 44]	[(3446)2; 3636; (44)2]	[(3446)2; 3636; (44)2]	[3446; (3636)2; (44)2]
[(3446)2; 3636; (44)2]	[(3446)2; 3636; (44)2]	[3446; (3636)2; (44)2]	[36; (3342)2; (44)2]	[(36)2; 3342; (44)2]
[(36)2; 3342; (44)2]	[36; (3342)2; (44)2]	[36; (3342)2; (44)2]	[(3446)2; 3636; (44)2]	[(36)2; (3342)2; 44]
[(36)2; (3342)2; 44]	[(36)2; (3342)2; 44]	[(36)2; (3342)2; 44]	[(33434)2; 3262; (3446)2]	[3342; (3262)2; (3446)2]
[3342; (3262)2; (3446)2]	[3262; (3446)2; (3636)2]	[(3262)2; 3446; (3636)2]	[(3262)2; 3446; (3636)2]	[(3464)2; (3446)2; 3636]
[3262; (3446)2; (3636)2]	[3262; (3446)2; (3636)2]	[(346)2; (3446)2; 3636]	[(346)2; (3446)2; 3636]	[(346)2; (3446)2; 3636]
[(346)2; (3446)2; 3636]	[(3342)2; (3446)2; 3636]	[(3342)2; (3446)2; 3636]	[(346)2; (3342)2; 3446]	[(346)2; 3342; (3446)2]
[(36)2; (346)2; 3262]	[36; (346)2; (3262)2]	[(36)2; 346; (3262)2]
[36; (346)2; (3262)2]	[346; (3262)2; (3636)2]	[(346)2; (3262)2; 3636]	[36; (346)2; (3262)2]	[(346)2; 3262; (3636)2]
[(346)2; (3262)2; 3636]	[(36)2; (346)2; 3262]	[(36)2; (346)2; 3262]	[(36)2; (346)2; 3636]	[(36)2; (346)2; 3636]
[36; (346)2; (3342)2]	[(36)2; (346)2; 3262]	[36; (346)2; (3262)2]	[36; (346)2; (3262)2]	[346; (3342)2; (3636)2]
[346; (3342)2; (3636)2]	[(36)2; 346; (3636)2]	[(36)2; (346)2; 3636]	[(36)2; 3342; (33434)2]

5-однородные мозаики, 2 типа вершин (4:1) и (3:2)

Существует 74 5-однородные мозаики с 2 видами вершин, 27 мозаик с отношением 4:1 и 47 с отношением 3:2 каждого вида вершин.

5-однородные мозаики (4:1)

[(3464)4; 46.12]	[343.12; (3.12.12)4]	[36; (33434)4]	[36; (33434)4]	[(36)4; 346]
[(36)4; 346]	[(36)4; 346]	[36; (346)4]	[3262; (3636)4]	[(346)4; 3262]
[(346)4; 3262]	[(346)4; 3636]	[3262; (3636)4]	[3446; (3636)4]	[3446; (3636)4]
[(3342)4; 33434]	[3342; (33434)4]
[3342; (44)4]	[3342; (44)4]	[(3342)4; 44]	[(3342)4; 44]	[(3342)4; 44]
[36; (3342)4]	[36; (3342)4]	[36; (3342)4]	[(36)4; 3342]	[(36)4; 3342]

Существует 29 5-однородных мозаик с отношением видов вершин 3:2.

5-однородные мозаики (3:2)

[(3464)2; (46.12)3]	[(3464)2; (46.12)3]	[(3464)3; (3446)2]	[(33434)2; (3464)3]	[(33434)3; (3464)2]
[(36)2; (346)3]	[(36)2; (346)3]	[(36)3; (346)2]	[(36)3; (346)2]	[(36)3; (346)2]
[(36)3; (346)2]	[(36)2; (346)3]	[(36)2; (346)3]	[(36)2; (346)3]
[(3262)2; (3636)3]	[(346)3; (3636)2]	[(346)3; (3636)2]	[(346)2; (3636)3]
[(3446)3; (3636)2]	[(3446)2; (3636)3]	[(3446)3; (3636)2]	[(3446)2; (3636)3]	[(3446)2; (3636)3]
[(3342)3; (33434)2]	[(3342)3; (33434)2]	[(3342)2; (33434)3]	[(3342)2; (33434)3]
[(3342)2; (44)3]	[(3342)2; (44)3]	[(3342)2; (44)3]	[(3342)3; (44)2]	[(3342)2; (44)3]
[(3342)3; (44)2]	[(3342)2; (44)3]	[(3342)2; (44)3]	[(3342)3; (44)2]	[(3342)3; (44)2]
[(36)2; (3342)3]	[(36)2; (3342)3]	[(36)2; (3342)3]	[(36)2; (3342)3]	[(36)3; (3342)2]
[(36)3; (3342)2]	[(36)3; (3342)2]	[(36)3; (3342)2]	[(36)3; (3342)2]	[(36)3; (3342)2]

k-однородные мозаики более высокого порядка

k-однородные мозаики перечислены вплоть до 6. Существует 673 6-однородные мозаики евклидовой плоскости. Исследования Брайана Гейлбаха воспроизвели список Кротенхирдта из 10 6-однородных мозаик с 6 различными видами вершин, 92 с 5 видами, 187 с 4 видами, 284 с 3 видами и 100 с 2 видами вершин.

Мозаики плиток, не соединённых ребро-к-ребру

Выпуклые правильные многоугольники могут образовывать мозаики плоскости, когда соединение многоугольников не осуществляется ребро-к-ребру. Такие мозаики можно считать мозаиками с соединением ребро-к-ребру, но многоугольники будут неправильными и имеющими рёбра, лежащие на одной прямой.

Существует семь семейств с параметром, определяющим коэффициент наложения рёбер смежных плиток или отношение длин рёбер различных плиток. Два этих семейства образуются сдвигом квадратов, постоянным или зигзагообразным. Грюнбаум и Шепард называет эти мозаики однородными, хотя это противоречит определению однородности Коксетером, которое требует соединение ребро-к-ребру^[7]. Такие равноугольные мозаики, фактически, топологически идентичны однородным мозаикам с различными геометрическими пропорциями.

Периодические изогональные мозаики
из выпуклых правильных многоугольников, не соединённых ребро-к-ребру

1	2	3	4	5	6	7
Ряды четырёх- угольников с горизонтальными сдвигами		Ряды треугольников с горизонтальными сдвигами	Мозаика из квадратов	Три шестиугольника, окружающих каждый треугольник	Шесть треугольников, окружающих каждый шестиугольник	Треугольники трёх размеров
cmm (2*22)	p2 (2222)	cmm (2*22)	p4m (*442)	p6 (632)		p3 (333)
Шестиугольная мозаика		Квадратная мозаика (вырожденная)	Усечённый квадратный паркет[англ.]	Усечённый шестиугольный паркет[англ.]	Шестиугольная мозаика	Тришестиугольная мозаика

См. также

• Однородные мозаики на гиперболической плоскости
• Список выпуклых однородных мозаик^[англ.]
• Символ Витхоффа^[англ.]
• Замощение
• Группа обоев
• Платоновы тела
• Полуправильный многогранник (включая Архимедовы тела)
• Геометрия Лобачевского
• Мозаика Пенроуза
• Замощение прямоугольниками^[англ.]

Примечания

1. Critchlow, 2000, с. 60-61.
2. k-uniform tilings by regular polygons Архивировано 30 июня 2015 года. Nils Lenngren, 2009
3. Critchlow, 2000, с. 62-67.
4. Grünbaum, Shephard, 1990, с. 65-67.
5. In Search of Demiregular Tilings  (неопр.). Дата обращения: 16 января 2016. Архивировано из оригинала 7 мая 2016 года.
6. Chavey, 1989.
7. Tilings by regular polygons Архивная копия от 3 марта 2016 на Wayback Machine p.236

• Grünbaum, Branko, G. C. Shephard^[англ.]. Tilings and Patterns. — W. H. Freeman and Company, 1990. — ISBN 0-7167-1193-1.
• Branko Grünbaum, Geoffrey C. Shephard. Tilings by regular polygons // Math. Mag.. — 1977. — Т. 50. — С. 227–247. — doi:10.2307/2689529.
• Branko Grünbaum, G. C. Shephard. The ninety-one types of isogonal tilings in the plane // Trans. Am. math. Soc.. — 1978. — Т. 252. — С. 335–353. — doi:10.1090/S0002-9947-1978-0496813-3.
• I. Debroey, F. Landuyt. Equitransitive edge-to-edge tilings // Geometriae Dedicata. — 1981. — Т. 11, вып. 1. — С. 47–60. — doi:10.1007/BF00183189.
• Ding Ren, John R. Reay. The boundary characteristic and Pick's theorem in the Archimedean planar tilings // J. Combinat. Theory A. — 1987. — Т. 44, вып. 1. — С. 110–119. — doi:10.1016/0097-3165(87)90063-X.
• D. Chavey. Tilings by Regular Polygons—II: A Catalog of Tilings // Computers & Mathematics with Applications. — 1989. — Т. 17. — С. 147–165. — doi:10.1016/0898-1221(89)90156-9.
• Keith Critchlow. Order in Space: A design source book. — New York,: Thames & Hudson, 2000. — ISBN 0-500-34033-1. Reprint 1969 London ISBN=9-780-500-34033-2
• Duncan MacLaren Young Sommerville. An Introduction to the Geometry of n Dimensions. — Dover Publications, 1958. Глава X: The Regular Polytopes
• P. =Préa. Distance sequences and percolation thresholds in Archimedean Tilings // Mathl. Comput. Modelling. — 1997. — Т. 26. — С. 317–320. — doi:10.1016/S0895-7177(97)00216-1.
• Jurij Kovic. Symmetry-type graphs of Platonic and Archimedean solids // Math. Commun.. — 2011. — Т. 16, вып. 2. — С. 491–507.
• Daniel Pellicer, Gordon Williams. Minimal covers of the Archimedean Tilings // El. J. Combinat. — 2012. — Т. 19, вып. 3. — С. P6.
• Dale Seymour, Jill Britton. Introduction to Tessellations. — Palo Alto: Dale Seymour Publications, 1989. — С. 50–57. — ISBN 978-0866514613.

Ссылки

Euclidean and general tiling links:

• Dutch, Steve. Uniform Tilings  (неопр.). Дата обращения: 9 сентября 2006. Архивировано из оригинала 9 сентября 2006 года.
• Mitchell, K. Semi-Regular Tilings  (неопр.). Дата обращения: 9 сентября 2006.
• Weisstein, Eric W. Tessellation (англ.) на сайте Wolfram MathWorld.
• Weisstein, Eric W. Semiregular tessellation (англ.) на сайте Wolfram MathWorld.
  • Weisstein, Eric W. Demiregular tessellation (англ.) на сайте Wolfram MathWorld.